Решение типового варианта задания 3

Задание. Найти площадь фигуры, ограниченной линиями

y = x² + 2x – 16, 4x – y – 8 = 0.

Решение.

Построим схематичный чертеж фигуры (рис. 3).

· Уравнение y = x² + 2x – 16 задает параболу.

· Найдем координаты точки В (х_В, у_В) вершины параболы.

· Абсциссу вершины найдем по формуле .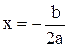

· Из уравнения параболы следует, что а = 1, b = 2, т.е.

.

· Подставляя в уравнение параболы x_В = 1 найдем ординату вершины y_В = (– 1)² + 2×(– 1) – 16 = –17.

· Таким образом, вершина параболы  находится в точке B(– 1; –17).

· Так как а = 1 > 0, то ветви параболы направлены вверх.

· Найдем абсциссы точек (у = 0) пересечения параболы с осью Ох, решив уравнение:

x² + 2x – 16 = 0,

Д = 2² – 4×1× (– 16) = 4 + 64 = 68,

и .

Таким образом, парабола пересекается с осью Ох в точках P( ; 0) и Q( 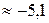; 0) .

· Строим параболу (рис. 34).

· Уравнение 4х – у – 8 = 0 задает прямую. Для ее построения достаточно знать координаты двух любых точек. Строим таблицу:

 

х	0	2
у	–8	0

 

Значения х берутся любые, а значения у вычисляются:

х = 0: 4×0 – у – 8 = 0

– у = 8

у = – 8;

х = 2: 4×2 – у – 8 = 0

8 – у – 8 = 0

у = 0.

Таким образом, прямая проходит через точки N(0, – 8) и M(2, 0). Строим прямую (рис. 34).

· Найдем точки пересечения параболы и прямой, решая систему уравнений:

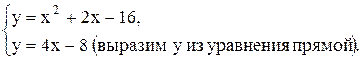
2. Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:

x² + 2x – 16 = 4x – 8,

x² – 2x – 8 = 0,

Д = (– 2)² – 4×(– 8) = 36

,      .

Таким образом, парабола и прямая пересекаются в точках с абсциссами  и  (см. рис. 3).

 

 

Найдем площадь фигуры.

· Проецируя фигуру на ось абсцисс, видим, что искомая площадь – это площадь фигуры, заключенной между прямой и параболой. При этом на отрезке [–2; 4]:

.

·  Получаем:

    

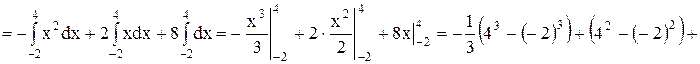
Ответ: .

 

Задание 4. Найти площадь фигуры, ограниченной линиями.

№ варианта	Уравнение линий, ограничивающих фигуру	№ варианта	Уравнение линий, ограничивающих фигуру
1	,	16	,
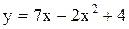
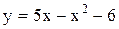
2	,	17	,
3	,	18	,
4	,	19	,
5	,	20	,

Решение типового варианта задание 4

Задание. Найти площадь фигуры, ограниченной линиями

, .

Решение.

Сделаем чертеж.

·  –этоуравнение параболы, ветви которой направлены     (а = – 1 < 0) вниз. Найдем координаты вершины параболы (а = – 1,      b = 0, c = 4):

Таким образом, координаты вершины параболы находятся в точке С(0; 4).

Найдем точки пересечения параболы с осью Ох:

0 = 4 – x² Þ x² = 4 Þ x = ± 2.

Таким образом, парабола пересекается с осью Ох в точках А(2; 0) и     B(– 2; 0). Строим параболу (см рис. 35).

·   – это уравнение параболы, ветви которой направлены      (а = 1 > 0) вверх.

Найдем координаты вершины параболы (а = 1, b = –2, c = 0):

Таким образом, координаты вершины параболы находятся в точке D(1; –1).

Найдем точки пересечения параболы с осью Ох:

0 = х² – 2х Þ х(х – 2) = 0 Þ х₁ = 0 или х₂ = 2.

Таким образом, парабола пересекается с осью Ох в точках О(0; 0) и       А (2;0).

Строим параболу (см. рис. 4)

 

2. Найдем абсциссы точек пересечения заданных линий, решив систему уравнений (точки P и A):

Д = (– 1)² – 4×1×(– 2) = 9.

х₁ = , х₂ = .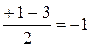

Таким образом, данные линии, представляющие собой параболы, пересекаются в точках с абсциссами х₁ = 2 и х₂ = – 1 (см рис. 4).

3. Проецируя фигуру на ось абсцисс, видим, что искомая площадь – это площадь фигуры, заключенной между кривыми. При этом на отрезке [– 1; 2]:

.

Получаем: .    

Ответ: .

Задание 5. Найти площади плоских фигур, ограниченных линиями, заданными уравнениями.

 

---

Дата добавления: 2019-02-26; просмотров: 150; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!