Задачи для самостоятельного решения
Вариант 1
По совокупности 30 предприятий концерна изучается зависимость прибыли y (тыс. руб.) от выработки продукции на одного работника x1 (ед.) и индекса цен на продукцию x2 (%):
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| y | 250 | 38 | 
|
| x1 | 47 | 12 | 
|
| x2 | 112 | 21 | 
|
Задание
1. Постройте линейные уравнения парной регрессии, оцените их значимость с помощью F-критерия Фишера.
2. Найдите уравнение множественной регрессии в стандартизованном и натуральном масштабе.
3. Рассчитайте множественный коэффициент корреляции, общий и частный критерии Фишера и сделайте выводы.
Вариант 2
По 30 заводам, выпускающим продукцию A, изучается зависимость потребления электроэнергии y (тыс. кВт/ч) от производства продукции – x1 (тыс. ед.) и уровня механизации – x2 (%):
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| y | 1000 | 27 | 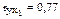
|
| x1 | 420 | 45 | 
|
| x2 | 41,5 | 18 | 
|
Задание
1. Постройте уравнение множественной регрессии в стандартизованном и натуральном масштабе.
2. Определите показатели частной и множественной корреляции.
3. Найдите частные коэффициенты эластичности и сравните их с
b-коэффициентами.
4. Рассчитайте общий и частные критерии Фишера и сделайте выводы.
Вариант 3
Изучается зависимость по 25 предприятиям концерна потребления материалов y (т) от энерговооруженности труда x1 (кВт/ч на одного рабочего) и объема произведенной продукции x2 (тыс. ед.):
|
|
|
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| y | 1000 | 27 | 
|
| x1 | 420 | 45 | 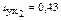
|
| x2 | 41,5 | 18 | 
|
Задание
1. Постройте уравнение множественной регрессии и поясните экономический смысл его параметров.
2. Определите частные коэффициенты эластичности и стандартизованные коэффициенты регрессии.
3. Найдите частные и множественный коэффициенты корреляции.
4. Оцените значимость уравнения регрессии с помощью F-критерия Фишера.
Вариант 4
Имеется информация по 25 наблюдениям:
| Признак | Среднее значение | Коэффициент вариации, % | Уравнение регрессии |
| y | 35 | 20 | 
|
| x1 | 16 | 30 | 
|
| x2 | 8 | 10 | 
|
Задание
1. Оцените значимость каждого уравнения регрессии, если известно, что  .
.
2. Оцените значимость коэффициентов регрессии с двумя объясняющими переменными.
3. Определите показатели частной корреляции.
4. Найдите частные коэффициенты эластичности.
Вариант 5
Имеется информация по 22 наблюдениям:
| Признак | Среднее значение | Коэффициент вариации, % | Уравнение регрессии |
| y | 23 | 20 | 
|
| x1 | 6 | 40 | 
|
| x2 | 8 | 10 | 
|
Задание
|
|
|
1. Оцените значимость каждого уравнения регрессии, если известно, что  .
.
2. Оцените значимость коэффициентов регрессии с двумя объясняющими переменными.
3. Найдите скорректированный коэффициент множественной корреляции.
4. Определите показатели частной корреляции.
Вариант 6
По 50 семьям изучалось потребление мяса – y (кг на душу населения) от дохода – x1 (руб. на одного члена семьи) и от потребления рыбы – x2 (кг на душу населения):
Уравнение регрессии 
|
| Стандартные ошибки параметров 20 0, 01 0,25 |
| Множественный коэффициент корреляции 0,85 |
Задание
1. Используя t-критерий Стьюдента, оцените значимость параметров уравнения.
2. Рассчитайте F-критерий Фишера.
3. Оцените по частным F-критериям Фишера целесообразность включения в модель фактора x1 после фактора x2 и фактора x2 после фактора x1.
Вариант 7
По 40 предприятиям одной отрасли исследовалась зависимость производительности труда – y от уровня квалификации рабочих – x1 и от энерговооруженности их труда – x2:
Уравнение регрессии 
|
| Стандартные ошибки параметров 0,5 2 ? |
| t-критерий для параметров 3 ? 5 |
| Множественный коэффициент корреляции 0,85 |
Задание
|
|
|
1. Определите параметр a и заполните пропущенные значения.
2. Оцените значимость уравнения в целом, используя значение множественного коэффициента корреляции.
3. Какой из факторов оказывает более сильное воздействие на результат?
Вариант 8
По 30 заводам, выпускающим продукцию A, изучается зависимость потребления электроэнергии y (тыс. кВт/ч) от производства продукции – x1 (тыс. ед.) и уровня механизации – x2 (%):
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| y | 1000 | 27 | 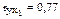
|
| x1 | 420 | 40 | 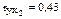
|
| x2 | 41,5 | 15 | 
|
Задание
5. Постройте уравнение множественной регрессии в стандартизованном и натуральном масштабе.
6. Определите показатели частной и множественной корреляции.
7. Найдите частные коэффициенты эластичности и сравните их с
b-коэффициентами.
8. Рассчитайте общий и частные критерии Фишера и сделайте выводы.
Вариант 9
Имеется информация по 25 наблюдениям:
| Признак | Среднее значение | Коэффициент вариации, % | Уравнение регрессии |
| y | 35 | 18 | 
|
| x1 | 15 | 30 | 
|
| x2 | 8 | 10 | 
|
Задание
|
|
|
5. Оцените значимость каждого уравнения регрессии, если известно, что  .
.
6. Оцените значимость коэффициентов регрессии с двумя объясняющими переменными.
7. Определите показатели частной корреляции.
8. Найдите частные коэффициенты эластичности.
Вариант 10
По 40 предприятиям одной отрасли исследовалась зависимость производительности труда – y от уровня квалификации рабочих – x1 и от энерговооруженности их труда – x2:
Уравнение регрессии 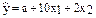
|
| Стандартные ошибки параметров 0,5 2 ? |
| t-критерий для параметров 3 ? 5 |
| Множественный коэффициент корреляции 0,85 |
Задание
4. Определите параметр a и заполните пропущенные значения.
5. Оцените значимость уравнения в целом, используя значение множественного коэффициента корреляции.
6. Какой из факторов оказывает более сильное воздействие на результат?
3. Системы одновременных уравнений
Теоретическое введение
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений:
· система независимых уравнений – когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:

Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;
· система рекурсивных уравнений – когда зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении:

Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;
· система взаимосвязанных (совместных) уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую:

Такая система уравнений называется структурной формой модели.
Эндогенные переменные – взаимозависимые переменные, которые определяются внутри модели (системы) у.
Экзогенные переменные – независимые переменные, которые определяются вне системы х.
Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы.
Коэффициенты а и b при переменных – структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы – приведенная форма модели:

где d – коэффициенты приведенной формы модели.
Необходимое условие идентификации – выполнение счетного правила:
D + 1 = Н – уравнение идентифицируемо;
D + 1 < Н – уравнение неидентифицируемо;
D + 1 > Н – уравнение сверхидентифицируемо,
где H – число эндогенных переменных в уравнении,
D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации – определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифи-цированных – двухшаговый метод наименьших квадратов.
Косвенный МНК состоит в следующем:
· составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК;
· путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
· составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК;
· выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и находят расчетные значения по соответствующим уравнениям приведенной формы модели;
· обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.
Решение типовой задачи
Постановка задачи
Требуется:
1. Оценить следующую структурную модель на идентификацию:

2. Исходя из приведенной формы модели уравнений

найти структурные коэффициенты модели.
Решение задачи
1. Модель имеет три эндогенные (y1,y2,y3) и три экзогенные (x1,x2,x3) переменные.
Проверим каждое уравнение системы на необходимое (H) и достаточное (Д) условия идентификации.
Первое уравнение.
Н: эндогенных переменных – 2 (y1,y3),
отсутствующих экзогенных – 1 (x2).
Выполняется необходимое равенство 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют y2 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| y2 | x2 | |
| Второе | -1 | a22 |
| Третье | b32 | 0 |
 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Второе уравнение.
Н: эндогенных переменных – 3 (y1,y2,y3),
отсутствующих экзогенных – 2 (x1, x3).
Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо.
Д: во втором уравнении отсутствуют x1 и x3. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| x1 | x3 | |
| Первое | a11 | a13 |
| Третье | a31 | a33 |
 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.
Третье уравнение.
Н: эндогенных переменных – 2 (y2,y3),
отсутствующих экзогенных – 1 (x2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в третьем уравнении отсутствуют y1 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| y1 | x2 | |
| Первое | -1 | 0 |
| Второе | b21 | a22 |
 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо.
Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.
2. Вычислим структурные коэффициенты модели:
a) из третьего уравнения приведённой формы выразим x2 (так как его нет в первом уравнении структурной формы):

Данное выражение содержит переменные y3, x1 и x3, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x2 в первое уравнение приведенной формы модели (ПФМ):

 – первое уравнение СФМ;
– первое уравнение СФМ;
б) во втором уравнении СФМ нет переменных x1 и x3 структурные параметры второго уравнения СФМ можно будет определить в два этапа:
Первый этап: выразим x1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:

Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует x3, которого нет в СФМ.
Выразим x3 из третьего уравнения ПФМ:
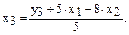
Подставим его в выражение x1:


Второй этап: аналогично, чтобы выразить x3 через искомое y1, y3 и x2, заменим в выражении x3 значение x1 на полученное из первого уравнения ПФМ:
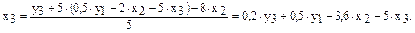
Следовательно,

Подставим полученные x1 и x3 во второе уравнение ПФМ:

 – второе уравнение СФМ.
– второе уравнение СФМ.
Это уравнение можно получить из ПФМ иным путём.
Суммируя все уравнения, получим

Далее из первого и второго уравнений ПФМ исключим x1, домножив первое уравнение на 3, а второе – на (–2) и просуммировав их:

Затем аналогичным путем из полученных уравнений исключаем x3, а именно:




в) из второго уравнения ПФМ выразим x2, так как его нет в третьем уравнении СФМ:

Подставим полученное выражение в третье уравнение ПФМ:

 – третье уравнение СФМ.
– третье уравнение СФМ.
Таким образом, СФМ примет вид

Дата добавления: 2019-02-26; просмотров: 606; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
