Множественная регрессия и корреляция

Теоретическое введение

Множественная регрессия – уравнение связи с несколькими независимыми переменными: , где у – зависимая переменная (результативный признак); х₁, х₂,…, х_p – независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще используются следующие функции:

· линейная – ;

· степенная – ;

· экспонента – ;

· гипербола – .

Можно использовать и другие функции, приводимые к линейному виду.

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:

Для ее решения может быть применен метод определителей:

, ,…, ,

где – определитель системы;

– частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизированном масштабе:

где , – стандартизированные переменные; – стандартизированные коэффициенты регрессии.

К уравнению множественной регрессии в стандартизированном масштабе применим МНК. Стандартизированные коэффициенты регрессии (b-коэффициенты) определяются из следующей системы уравнений:

Связь коэффициентов множественной регрессии b_i со стандартизированными коэффициентами описывается соотношением

Параметр а определяется как .

Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле

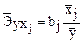Для расчета частных коэффициентов эластичности применяется следующая формула:

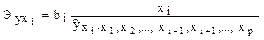Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:

Значение индекса множественной корреляции лежит в пределах от 0 до1 и должно быть больше или равно максимальному парному индексу корреляции:

Индекс множественной корреляции для уравнения в стандартизированном масштабе можно записать в виде

При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

где – определитель матрицы парных коэффициентов корреляции;

– определитель матрицы межфакторной корреляции.

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_i при неизменном уровне других факторов, можно определить по формуле

или по рекуррентной формуле:

Частные коэффициенты корреляции изменяются в пределах
от –1 до 1.

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции:

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле

где n – число наблюдений;m – число факторов.

Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:

Частный F -критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора x_i частный F-критерий определяется как

Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значения

где – средняя квадратичная шибка коэффициента регрессии b_i, она может быть определена по следующей формуле:

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности.

Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если .

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы были бы равны нулю. Так, для включающего три объясняющих переменных уравнения 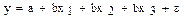матрица коэффициентов корреляции меду факторами имела бы определитель, равный 1:

так как и .

Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:

Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных . Доказано, что величина имеет приближенное распределение χ² с степенями свободы. Если фактическое значение χ² превосходит табличное (критическое) , то гипотеза H₀ отклоняется. Это означает, что , недиагональные нулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.

Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора x_j остатки 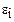имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность.

При нарушении гомоскедастичности мы имеем неравенства

При малом объеме выборки для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта. Основная идея теста Гольдфельда-Квандта состоит в следующем:

1) упорядочение n наблюдений по мере возрастания переменной х;

2) исключение из рассмотрения С натуральных наблюдений; при этом (n-C): 2>p, где p – число оцениваемых параметров;

3) разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и с большими значениями фактора х) и определение по каждой из групп уравнений регрессии;

4) определение остаточной суммы квадратов для первой (S1) и второй (S2) групп и нахождение их отношения: R=S1: S2.

При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F-критерию со степенями свободы ((n-C-2p):2) для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

Уравнения множественной регрессии могут включать в качестве независимых переменных качественные признаки (например, профессия пол, образование, климатические условия, отдельные регионы и т.д.). Чтобы ввести такие переменные в регрессионную модель, их необходимо упорядочить и присвоить им те или иные значения, т.е. качественные переменные преобразовать в количественные.

Такого вида сконструированные переменные принято в эконометрике называть фиктивными переменными. Например, включать в модель фактор «пол» в виде фиктивной переменной можно в следующем виде:

Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории (женский пол) к другой (мужской пол) при неизменных значениях остальных параметров. На основе t–критерия Стьюдента делается вывод о значимости влияния фиктивной переменной, существенности расхождения между категориями.

Решение типовых задач

Постановка задачи 1

По 30 территориям России имеются данные, представленные в таблице 2.1.

Таблица 2.1. Исходные данные задачи 1

Признак	Среднее значение	Среднее квадратическое отклонение	Линейный коэффициент парной корреляции
Среднедневной душевой доход, руб., у	86,8	11,44	–
Среднедневная плата одного работающего руб.,х₁	54,9	5,86	r_yx1 = 0,8405
Средний возраст безработного лет, х₂	33,5	0,58	r_yx2 = – 0,2101 r_x1х2= – 0,1160

Требуется:

1. Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с b₁и b₂, пояснить различия между ними.

2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами множественной корреляции, пояснить различия между ними.

3. Рассчитать общий и частные F-критерии Фишера.

Решение задачи 1

1. Линейное уравнение множественной регрессии y от х₁ и х₂ имеет вид: у=a+b₁x₁+b₂x₂. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: t_y=b₁t_x₁+b₂t_x₂.

Расчет b-коэффициентов выполним по формулам

;

Получим уравнение

t_y=0,8273t_x₁+0,1141t_x₂.

Для построения уравнения в естественной форме рассчитаем b₁ и b₂, используя формулы для перехода от b_i к b_i:

; _;

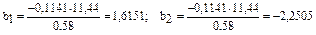Значение a определим из соотношения

;

Для характеристики относительной силы влияния x₁и x₂ на y рассчитаем средние коэффициенты эластичности:

С увеличением средней заработной платы x₁на 1% от её среднего уровня средний душевой доход у возрастает на 1,02% от всего среднего уровня; при повышении среднего возраста безработного x₂ на 1% среднедушевой доход у снижается на 0,87% от всего среднего уровня. Очевидно, что сила влияния средней заработной платы x₁на средний душевой доход у оказалась большей, чем сила влияния среднего возраста безработного x₂. К аналогичным выводам о силе связи приходим при сравнении модулей значений b₁ и b₂:

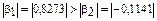Различия в силе влияния фактора на результат, полученные при сравнении и b_j, объясняются тем, коэффициент эластичности происходит из соотношения средних: , а b-коэффициент – из соотношения средних квадратических отклонений: .

2. Линейные коэффициенты частой корреляции здесь рассчитываются по рекуррентной формуле:

;

Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи ( = –0,116) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:

Расчёт линейного коэффициента множественной корреляции выполним с использованием коэффициентов r_yxj и b_j:

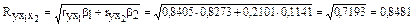Зависимость у от х₁ и х₂ характеризуется как тесная, в которой 72% вариации среднего душевного дохода определяются вариацией учтённых в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включённые в модель, составляют соответственно 28% от общей вариации у.

3. Общий F-критерий проверяет гипотезу Н₀ о статистической значимости уравнения регрессии и показателя тесноты связи (R²=0):

;

F_табл=3,4; a=0,05.

Сравнивая F_факт и F_табл, приходим к выводу о необходимости отклонить гипотезу Н₀, так как F_табл=3,4 < F_факт=34,6. С вероятностью
1-a=0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи R_yx₁_x_2,которые сформировались под неслучайным воздействием факторов х₁ и х₂.

Частные F-критерии – F_x₁ и F_x₂ оценивают статистическую значимость присутствия факторов х₁ и х₂ в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, то есть F_x₁ оценивает целесообразность включения в уравнение одного фактора х₁ после того, как в него был включён фактор х_2. Соответственно F_x₂ указывает на целесообразность включения в уравнение одного фактора х₂ после фактора х₁:

F_табл=4,21; a=0,05.

Сравнивая F_факт и F_табл, приходим к выводу о целесообразности включения в модель фактора х₁ после фактора х_2,так как
F_{х1 факт} = 64,9 > F_табл. Гипотезу Н₀ о несущественности прироста R²_y за счёт включения дополнительного фактора х₁ отклоняем и приходим к выводу о статистически подтверждённой целесообразности включении фактора х₁ после фактора х₂.

Целесообразность включения фактора х₂ после фактора х₁ проверяет F_x₂:

Низкое значение F_{х2 факт} (немногим больше 1) свидетельствует о статистической незначимости прироста r²_yx₁ за счёт включения фактора х₂ после фактора х_1.Следовательно, подтверждается нулевая гипотеза Н₀ о нецелесообразности включения в модель фактора х₂ (средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, надёжной и что нет необходимости улучшать её, включая дополнительный фактор х₂ (средний возраст безработного).

Постановка задачи 2

По 20 территориям России изучаются следующие данные: зависимость среднегодового дохода y (тыс. руб.) от доли занятых тяжелым физическим трудом в общей численности занятых x₁ (%) и от доли экономически активного населения в численности всего населения x₂ (%), представленные в таблице 2.2.

Таблица 2.2. Исходные данные задачи 2

Признак	Среднее значение	Среднее квадратическое отклонение	Характеристика тесноты связи	Уравнение связи
y	112,76	31,58	R_yx1x2=0,773
x₁	5,40	3,34	r_yx1=0,746
x₂	50,88	1,74	r_yx2=0,507 r_x1x2=0,432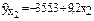

Требуется:

1. Составить таблицу дисперсионного анализа для проверки при уровне значимости a=0,05 статистической значимости уравнения множественной регрессии и его показателя тесноты связи.

2. С помощью частных F-критериев Фишера оценить, насколько целесообразно включение в уравнение множественной регрессии фактора x₁ после фактора x₂ и насколько целесообразно включение x₂ после x₁.

3. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов при переменных x₁ и x₂ множественного уравнения регрессии.

Решение задачи 2

1. Задача дисперсионного анализа состоит в проверке нулевой гипотезы H₀ о статистической незначимости уравнения регрессии в целом и показателя тесноты связи.

Анализ выполняется при сравнении фактического и табличного (критического) значений F-критерия Фишера. F_факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

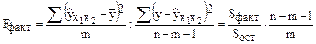Результаты дисперсионного анализа представлены в таблице 2.3.

Таблица 2.3. Результаты дисперсионного анализа

Вариация результата, y	Число степней свободы	Сумма квадратов отклонений, S	Дисперсия на одну степень свободы, S²	F_факт	F_табл a=0,05, k₁=2, k₂=17
Общая	df=n-1=19	19945,9	–	–	–
Факторная	k₁=m=2	11918,3	5959,15	12,62	3,59
Остаточная	k₂=n-m-1=17	8027,6	472,21	–	–

Сравнивая F_табл и F_факт, приходим к выводу о необходимости отклонить гипотезу H₀ и сделать вывод о статистической значимости уравнения регрессии в целом и значения 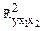, так как они статистически надежны и сформировались под систематическим действием неслучайных причин. Вероятность того, что допускаются ошибки при отклонении нулевой гипотезы, не превышает 5%, и это является достаточно малой величиной.

2. Частный F-критерий Фишера оценивает статистическую целесообразность включения фактора x₁ в модель после того, как в нее включен фактор x₂. Частный F-критерий Фишера строится как отношение прироста факторной дисперсии за счет дополнительно включенного фактора (на одну степень свободы) к остаточной дисперсии (на одну степень свободы), подсчитанной по модели с включенными факторами x₁ и x₂:

Результаты дисперсионного анализа представлены в таблице 2.4.

Таблица 2.4. Результаты дисперсионного анализа

Вариация результата, y	Число степней свободы	Сумма квадратов отклонений, S	Дисперсия на одну степень свободы, S²	F_факт	F_табл a=0,05, k₁=2, k₂=17
Общая	df=n-1=19	19945,9	–	–	–
Факторная В том числе: за счет x₂ за счет дополнительно включенного x₁	k₁=m=2 1 1	11918,3 5127,1 6791,2	5959,15 5127,1 6791,2	12,62 10,86 14,38	3,59 4,45 4,45
Остаточная	k₂=n-m-1	8027,6	472,21	–	–

Включение фактора x₁ после фактора x₂ оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, т.е. следствием дополнительного включения в модель систематически действующего фактора x₁, так как = 14,38 > F_табл = 4,45.

Аналогично проверим целесообразность включения в модель дополнительного фактора x₂ после включенного ранее фактора x₁.Расчет выполним с использованием показателей тесноты связи и :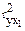

В силу того что = 1,73 < F_табл = 4,45, приходим к выводу, что включение x₂ после x₁ оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы был несущественен, статистически незначим, т.е. влияние x₂ не является устойчивым, систематическим. Вполне возможно было ограничиться построением линейного уравнения парной регрессии у от x₁.

3. Оценка с помощью t-критерия Стьюдента значимости коэффициентов b₁ и b₂ связана с сопоставлением их значений с величиной их случайных ошибок: m_b₁ и m_b₂. Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается более простой способ: расчет значения t-критерия Стьюдента для коэффициентов регрессии линейного уравнения как квадратного корня из соответствующего частного F-критерия Фишера:

Табличные (критические) значения t-критерия Стьюдента зависят от принятого уровня значимости a (обычно это 0,1; 0,05 или 0,01) и от числа степеней свободы (n-m-1), где n– число единиц совокупности, m – число факторов в уравнении.

В нашем примере a = 0,05; df = 20-3 = 17; t_табл = 2,10. Сравнивая t_табл и t_факт, приходим к выводу, что так как t_b₁ = 3,79 > 2,11 = t_табл, коэффициент b₁ является статистически значимым, надежным, на него можно опираться в анализе и прогнозе. Так как t_b₂ = 1,32 < 2,10 = t_табл, приходим к заключению, что величина b₂ является статистически незначимой, ненадежной в силу того, что она формируется преимущественно под воздействием случайных факторов. Еще раз подтверждается статистическая значимость влияния x₁ (доли занятых тяжелым физическим трудом) на у (среднедушевой доход) и ненадежность, незначимость влияния х₂ (доли экономически активного населения в численности всего населения).

Дата добавления: 2019-02-26; просмотров: 414; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!