Элементы теории игр в задачах моделирования экономических процессов

⇐ ПредыдущаяСтр 7 из 8Следующая ⇒

При решении экономических задач часто приходится анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные цели; это особенно характерно в условиях рыночной экономики. Такого рода ситуации называются конфликтными. Математической теорией конфликтных ситуаций является теория игр. В игре могут сталкиваться интересы двух (игра парная) или нескольких (игра множественная) противников; существуют игры с бесконечным множеством игроков. Если во множественной игре игроки образуют коалиции, то игра называется коалиционной; если таких коалиций две, то игра сводится к парной.

На промышленных предприятиях теория игр может применяться для выбора оптимальных решений, например при создании рациональных запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличения запасов, гарантирующих бесперебойную работу производства, и сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как выбор для посева одной из возможных культур, урожай которых зависит от погоды, если известны цена единицы той или иной культуры и средняя урожайность каждой культуры в зависимости от погоды (например, будет ли лето засушливым, нормальным или дождливым); в этом случае одним из игроков выступает сельскохозяйственное предприятие, стремящееся обеспечить наибольший доход, а другим - природа.

Решение подобных задач требует полной определенности в формулировании их условий (правил игры) установления количества игроков, выявления возможных стратегий игроков, возможных выигрышей (проигрыш понимается как отрицательный выигрыш). Важным элементом в условии игровых задач является стратегия, т.е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор действий данного игрока. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а ее элементы - чистыми стратегиями. Количество стратегий у каждого игрока может быть конечным и бесконечным, в зависимости от этого игры подразделяются на конечные и бесконечные.

Важными являются понятия оптимальной стратегии, цены игры, среднего выигрыша. Эти понятия находят отражение в определении решения игры, стратегии Р * и Q' первого и второго игроков соответственно называются их оптимальными стратегиями, а число V - ценой игры, если для любых стратегий Р первого игрока и любых стратегий Q второго игрока выполняются неравенства

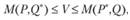(8.64)

где М(Р, Q) означает математическое ожидание выигрыша (средний выигрыш) первого игрока, если первым и вторым игроками избраны соответственно стратегии Р и Q.

Из неравенств (8.64) следует, в частности, что V = М(Р*, Q*), т.е. цена игры равна математическому ожиданию выигрыша первого игрока, если оба игрока изберут оптимальные для себя стратегии.

Одним из основных видов игр являются матричные игры, которыми называются парные игры с нулевой суммой (один игрок выигрывает столько, сколько проигрывает другой) при условии, что каждый игрок имеет конечное число стратегий. В этом случае парная игра формально задается матрицей А = (а_ij), элементы которой а_ij определяют выигрыш первого игрока (и соответственно проигрыш второго), если первый игрок выберет i-ю стратегию ( 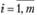), а второй - j-ю стратегию ( 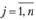). Матрица А называется матрицей игры, или платежной матрицей.

Рассмотрим построение платежной матрицы на примере.

Пример 8.8. На базе торговой фирмы имеется п типов товара ассортиментного минимума. В магазин фирмы должен быть завезен только один из этих типов товара. Если товар типа j( 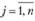) будет пользоваться спросом, то магазин от его реализации получит прибыль Р_j. Если же этот товар не будет пользоваться спросом, то издержки на его хранение принесут магазину убыток q_j. Требуется выбрать тип товара, который целесообразно завезти в магазин.

В условиях неопределенного покупательского спроса конфликтная ситуация товароснабжения формализуется матричной игрой. Пусть первый игрок - магазин, второй игрок - покупательский спрос. Каждый из игроков имеет по п стратегий. Завоз i-го товара - i-я стратегия первого игрока, спрос на j-й товар - j-я стратегия второго игрока. Тогда матрица выигрышей первого игрока имеет вид квадратной матрицы n-го порядка:

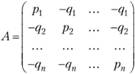
Существует ряд методов решения матричных игр. Если матрица игры имеет одну из размерностей, равную двум (у одного из игроков имеется только две стратегии), то решение игры может быть получено графически. Известно несколько методов приближенного решения матричной игры, например метод Брауна. Применяются также методы линейного программирования.

В качестве примера рассмотрим решение игры, когда матрица игры имеет так называемую седловую точку.

Пример 8.9. Матрица игры имеет вид

Минимальный элемент первой строки (первой стратегии первого игрока) равен 2, второй - 5, третьей - 4; максимальное значение из этих величин равно 5. Максимальный элемент первого столбца (первой стратегии второго игрока) равен 10, второго - 10; третьего - 5, четвертого - 14, пятого - 12; минимальное значение из них равно 5. Следовательно, данная игра имеет седловую точку (2, 3) и задача разрешима в чистых стратегиях. Придерживаясь чисто второй стратегии, первый игрок обеспечивает себе выигрыш не меньший 5; второй игрок, применяя чистую третью стратегию, проигрывает не более 5. Обе стратегии i = 2 и j = 3 являются оптимальными для первого и второго игроков, при этом цена игры V = 5.

Во многих игровых задачах в сфере экономики неопределенность вызвана не сознательным противодействием противника, а недостаточной осведомленностью об условиях, в которых действуют стороны. Так, в рассматриваемых выше примерах были неизвестны заранее погода в некотором регионе, покупательский спрос на некоторую продукцию.

Подобного рода игры называются играми с природой. В этих случаях строки матрицы игры соответствуют стратегии игрока, а столбцы - состояниям "природы". В ряде случаев при решении такой игры рассматривают матрицу рисков.

При решении игр с природой используется также ряд критериев: критерий Сэвиджа, критерий Вальда, критерий Гурвица и др.

При максимипном критерии Вальда оптимальной считается та стратегия лица, принимающего решение (ЛПР), которая обеспечивает максимум минимального выигрыша; применяя этот критерий, ЛПР в большей степени ориентируется на наихудшие условия (этот критерий иногда называют критерием "крайнего пессимизма").

Критерий минимаксного риска Сэвиджа предполагает, что оптимальной является та стратегия, при которой величина риска в наихудшем случае минимальна.

При использовании критерия "пессимизм-оптимизм" Гурвица ЛПР выбирает некоторый так называемый коэффициент пессимизма q; при q = 1 критерий Гурвица приводит к критерию Вальда ("крайнего пессимизма"), а при q = 0 - к критерию "крайнего оптимизма". Рассмотрим пример использования указанных критериев в играх с природой.

Пример 8.10. Диспетчер автобусного парка (ЛПР) в летние месяцы в конце каждой недели должен принять решение о целесообразности выделения дополнительных автобусов на загородный маршрут. ЛПР имеет три варианта решений: увеличить количество автобусов на 10 (стратегия Р₁), увеличить это количество на 5 (стратегия Р₂) или оставить без изменения обычное число автобусов на линии (стратегия Р₃). Возможны два состояния погоды: Q₁ - плохая погода, Q₂ - хорошая погода, причем в момент принятия решения нет возможности определить ожидаемое состояние погоды. Если в выходные дни будет хорошая погода и много желающих выехать за город, а выделено мало автобусов, то парк понесет убытки, связанные с недополученной прибылью. Если же выделены дополнительные автобусы, а погода окажется плохой, то возникнут потери вследствие эксплуатации незаполненных автобусов.

Пусть на основе анализа статистических данных за определенный период установлена функция потерь для возможных комбинаций состояний природы и решений ЛПР в виде матрицы игры A(P_iQ_j), в которой отрицательные значения показывают дополнительную прибыль, а положительные - потери:

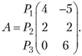
Если нет сведений о вероятностях различных состояний погоды, то по критерию Вальда и по критерию Сэвиджа оптимальной является стратегия Р₂. По критерию Гурвица при "коэффициенте пессимизма" q = 1 оптимальной окажется стратегия Р₂, а при q = 0 - стратегия Р₁.

Рассмотрим в заключение конкретный числовой пример решения задачи принятия решения в экономике методами теории игр.

Пример 8.11. Швейное предприятие, выпускающее детские платья и костюмы, реализует свою продукцию через фирменный магазин. Сбыт продукции зависит от состояния погоды. По данным прошлых наблюдений, предприятие в течение апреля - мая в условиях теплой погоды может реализовать 600 костюмов и 1975 платьев, а при прохладной погоде - 1000 костюмов и 625 платьев. Известно, что затраты на единицу продукции в течение указанных месяцев составили для костюмов 27 руб., дня платьев 8 руб., а цена реализации равна соответственно 48 руб. и 16 руб. (цифры условные).

Задача заключается в максимизации средней величины прибыли от реализации выпущенной продукции с учетом неопределенности погоды в рассматриваемые месяцы. Таким образом, служба маркетинга предприятия должна в этих условиях определить оптимальную стратегию предприятия, обеспечивающую при любой погоде определенный средний доход. Решим эту задачу методами теории игр, игра в этом случае будет относиться к типу игр с природой.

Предприятие располагает в этих условиях двумя чистыми стратегиями: стратегия А - в расчете на теплую погоду и стратегия Б - в расчете на холодную погоду. Природу будем рассматривать как второго игрока также с двумя стратегиями: прохладная погода (стратегия В) и теплая погода (стратегия Г). Если предприятие выберет стратегию А, то в случае прохладной погоды (стратегия природы В) доход составит

600(48 - 27) + 625(16 - 8) - (1975 - 625)8 = 6800 руб.,

а в случае теплой погоды (стратегия природы Г) доход будет равен

600(48 - 27) + 1975(16 - 8) = 28 400 руб.

Если предприятие выберет стратегию Б, то реализация продукции в условиях прохладной погоды даст доход

1000(48 - 27) + 625(16 - 8) = 26 000 руб.,

а в условиях теплой погоды

600(48 - 27) + 625(16 - 8) - (1000 - 600)27 = 6800 руб.

Следовательно, матрица данной игры (платежная матрица) имеет вид

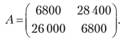
Первая и вторая строки этой матрицы соответствуют стратегиям А и Б предприятия, а первый и второй столбцы - стратегиям В и Г природы.

По платежной матрице видно, что первый игрок (предприятие) никогда не получит доход меньше 6800 руб. Но если погодные условия совпадают с выбранной стратегией, то выручка (выигрыш) составит 26 000 или 28 400 руб. Отсюда можно сделать вывод, что в условиях неопределенности погоды наибольший гарантированный доход предприятие обеспечит, если будет попеременно применять то стратегию А, то стратегию Б. Такая стратегия, как отмечалось выше, называется смешанной. Оптимизация смешанной стратегии позволит первому игроку всегда получать среднее значение выигрыша независимо от стратегии второго игрока.

Пусть х означает частоту применения первым игроком стратегии А, тогда частота применения им стратегии Б равна (1 - х). В случае оптимальной смешанной стратегии первый игрок (предприятие) получит и при стратегии В (холодная погода), и при стратегии Г (теплая погода) второго игрока одинаковый средний доход:

6800x + 26 000(1 - x) = 28 400x + 6800(1 - х).

Отсюда можно найти, что х = 8/17; 1 - х = 9/17. Следовательно, первый игрок, применяя чистые стратегии А к Б в соотношении 8:9, будет иметь оптимальную смешанную стратегию, обеспечивающую ему в любом случае средний доход в сумме 6800 - 8/17 + 26 000 - 9/17 = 16 965 руб.; эта величина и будет в данном случае ценой игры.

Легко рассчитать, какое количество костюмов и платьев должно выпускать предприятие при оптимальной стратегии: (600 костюмов + 1975 платьев) · 8/17 + (1000 костюмов + 625 платьев) · 9/17 = 812 костюмов + 1260 платьев. Следовательно, оптимальная стратегия предприятия заключается в выпуске 812 костюмов и 1260 платьев, что обеспечит ему при любой погоде средний доход в сумме 16 965 руб.

Дата добавления: 2019-02-26; просмотров: 194; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 Следующая ⇒

Мы поможем в написании ваших работ!