Функции покупательского спроса

Стр 1 из 8Следующая ⇒

Лекция 8 Некоторые прикладные и теоретические модели микро- и макроэкономических процессов

- Моделирование спроса и потребления

- Модели управления запасами Моделирование систем массового обслуживания

- Элементы теории игр в задачах моделирования экономических процессов

- Динамические модели макроэкономики

После изучения материала этой главы студенты должны:

знать:

o общие подходы к моделированию потребления и спроса и основные типы функций покупательского спроса:

o принципиальные системы и модели управления запасами;

o основные типы систем массового обслуживания (СМО) и методы расчета их характеристик;

o элементы теории игр и особенности применения этой теории в экономических исследованиях;

o структуру основных динамических макроэкономических моделей и системы предположений, лежащих в их основе;

уметь:

o использовать конкретные функции покупательского спроса для анализа и прогнозирования этого спроса;

o решать задачи управления запасами при различных предположениях о размере заказа и его периодичности;

o находить основные характеристики СМО различных типов;

o применять элементы теории игр для принятия решения в условиях неопределенности и риска;

o формулировать основные виды макроэкономических моделей (Кейнса, Самуэльсона - Хикса, Солоу);

владеть:

o понятийными аппаратами моделей спроса и потребления, управления запасами, систем массового обслуживания, а также основными элементами теории игр;

o навыками моделирования макроэкономических процессов.

Моделирование спроса и потребления

Целевая функция потребления и моделирование поведения потребителей

В условиях рыночной системы управления производственной и сбытовой деятельностью предприятий и фирм в основе принятия хозяйственных решений лежит рыночная информация, а обоснованность решений проверяется рынком в ходе реализации товаров и услуг. При таком подходе начальным пунктом всего цикла предпринимательской деятельности становится изучение потребительского спроса. Рассмотрим некоторые вопросы моделирования спроса и потребления.

Уровень удовлетворения материальных потребностей общества (уровень потребления) можно выразить целевой функцией потребления U = U(Y), где вектор переменных Y > 0 включает разнообразные виды товаров и услуг. Ряд свойств этой функции удобно изучать, используя геометрическую интерпретацию уравнений U(Y) = С, где С - меняющийся параметр, характеризующий значение (уровень) целевой функции потребления; в качестве величины С может выступать, например, доход или уровень материального благосостояния.

В пространстве потребительских благ каждому уравнению U(Y) = С соответствует определенная поверхность равноценных, или безразличных, наборов благ, которая называется поверхностью безразличия. Для наглядности рассмотрим пространство двух благ, например, в виде двух агрегированных групп товаров: продукты питания (y₁) и непродовольственные товары, включая услуги (y₂) Тогда уровни целевой функции потребления можно изобразить на плоскости в виде кривых безразличия, соответствующих различным значениям С (рис. 8.1, где С₁< С₂ < С₃).

Будем далее пользоваться термином "кривые безразличия" вне зависимости от размерности пространства потребительских благ (количества групп товаров).

Из основных свойств целевой функции потребления отметим следующие:

1) функция U(Y) является возрастающей функцией всех своих аргументов, т.е. увеличение потребления любого блага при неизменней уровне потребления всех других благ увеличивает значение данной функции. Поэтому более удаленная от начала координат кривая безразличия соответствует большему значению целевой функции потребления, а сам процесс максимизации этой функции на некотором ограниченном множестве допустимых векторов Y можно интерпретировать как нахождение допустимой точки, принадлежащей кривой безразличия, максимально удаленной от начала координат;

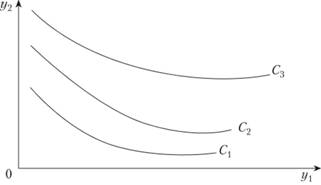
Рис. 8.1

2) кривые безразличия не могут пересекаться, т.е. через одну точку пространства благ (товаров, услуг) можно провести только одну поверхность безразличия. В противном случае один и тот же набор благ одновременно соответствовал бы нескольким разным уровням материального благосостояния;

3) кривые безразличия имеют отрицательный наклон к каждой оси координат, при этом абсолютный наклон кривых уменьшается при движении в положительном направлении по каждой оси, т.е. кривые безразличия являются выпуклыми кривыми.

Методы построения целевой функции потребления основаны на обобщении опыта поведения потребителей и тенденций покупательского спроса в зависимости от уровня благосостояния. В качестве примера приведем квадратичную целевую функцию потребления для трех агрегированных групп товаров, построенную на основе обработки данных бюджетной статистики:

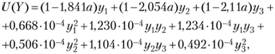
где:

параметр а означает число детей в семье;

у₁ - потребление продуктов питания;

у₂ - потребление промышленных товаров;

у₃ - потребление платных услуг (в стоимостном выражении).

Перейдем к вопросу моделирования поведения потребителей в условиях товарно-денежных отношений на базе целевой функции потребления. В основе модели поведения потребителей лежит гипотеза, что потребители, осуществляя выбор товаров при установленных ценах и имеющемся доходе, стремятся максимизировать уровень удовлетворения своих потребностей.

Пусть в пространстве п видов товаров исследуется поведение совокупности потребителей. Обозначим спрос потребителей через вектор Y = (у₁, у₂,…, у_n), а цены на различные товары - через вектор Р = (p₁, р₂,…, р_n). При величине дохода D потребители могут выбирать только такие комбинации товаров, которые удовлетворяют бюджетному ограничению . Предположим, что предпочтение потребителей на множестве товаров выражается целевой функцией потребления U(Y). Тогда простейшая модель поведения потребителей в векторной форме записи будет иметь вид:

(8.1)

Геометрическая интерпретация модели (8.1) для двух агрегированных групп товаров представлена на рис. 8.2.

Линия АВ (в других вариантах А₁В₁, А₂В₂) соответствует бюджетному ограничению и называется бюджетной линией (см. более подробно в параграфе 8.2). Выбор потребителей ограничен треугольником АОВ (А₁ОВ₁, А₂ОВ₂). Набор товаров М, соответствующий точке касания прямой АВ с наиболее отдаленной кривой безразличия, является оптимальным решением (в других вариантах это точки К и L). Легко заметить, что линии АВ и А₁В₁ соответствуют одному и тому же размеру дохода и разным ценам на товары у₁ и у₂; линия А₂В₂ соответствует большему размеру дохода.

Рис. 8.2

Опираясь на некоторые выводы теории нелинейного программирования, можно определить математические условия оптимальности решений для модели (8.1). С задачей нелинейного программирования связывается так называемая функция Лагранжа, которая для задачи (8.1) имеет вид

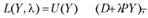
где множитель Лагранжа l является оптимальной оценкой дохода.

Обозначим частные производные функции U(Y) через 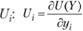. Эти производные интерпретируются как предельные полезные эффекты (предельные полезности) соответствующих потребительских благ и характеризуют прирост целевой функции потребления при увеличении использования i-го блага (товара) на некоторую условную "малую единицу".

Необходимыми условиями того, что вектор Y⁰ будет оптимальным решением, являются условия Куна - Таккера:

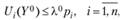
при этом

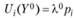, если (товар приобретается),

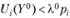, если 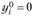(товар не приобретается), (8.2)

PY⁰= D.

Последнее из соотношений (8.2) соответствует полному использованию дохода, и для этого случая очевидно неравенство l⁰ > 0. Из условий оптимальности (8.2) следует, что

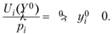
Это означает, что потребители должны выбирать товары таким образом, чтобы отношение предельной полезности к пене товара было одинаковым для всех приобретаемых товаров. Другими словами, в оптимальном наборе предельные полезности выбираемых товаров должны быть пропорциональны цепам.

Функции покупательского спроса

Функциями покупательского спроса (далее будем называть их просто функциями спроса) называются функции, отражающие зависимость объема спроса на отдельные товары и услуги от комплекса факторов, влияющих на него. Такие функции применяются в аналитических моделях спроса и потребления и строятся на основе информации о структуре доходов населения, ценах на товары, составе семей и других факторах. Рассмотрим построение функций спроса в зависимости от двух факторов - дохода и цен.

Пусть в модели (8.1) цены и доход рассматриваются как меняющиеся параметры. Переменную дохода будем обозначать Z. Тогда решением оптимизационной задачи (8.1) будет векторная функция Y⁰ = Y⁰ (Р, Z), компонентами которой являются функции спроса на определенный товар от цен и дохода:

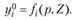
Рассмотрим частный случай, когда вектор цен остается неизменным, а изменяется только доход. Для двух товаров этот случай представлен на рис. 8.3. Если по оси абсцисс отложить количество единиц товара y_1, которое можно приобрести на имеющийся доход Z (точка В), а по оси ординат - то же самое для товара у₂ (точка А), то прямая линия АВ, называемая бюджетной линией, показывает любую комбинацию количеств этих двух товаров, которую можно купить за сумму денег Z. При увеличении дохода бюджетные линии перемещаются параллельно самим себе, удаляясь от начала координат. Вместе с ними перемещаются соответствующие кривые безразличия. Точками оптимума спроса потребителей для соответствующих размеров дохода будут в данном случае точки касания М₁, М₂, М₃. При нулевом доходе спрос на оба товара нулевой. Кривая, соединяющая точки О, М_ь М₂, М₃, является графическим отображением векторной функции спроса от дохода при заданном векторе цен.

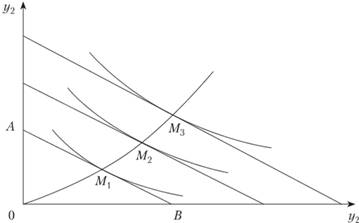
Рис. 8.3

Пример 8.1. Рассмотрим процесс аналитического построения функций спроса от дохода на основе модели (8.1) на конкретном условном примере. Пусть для двух товаров целевая функция потребления имеет вид 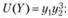вектор цен равен Р = (3; 6); величина дохода равна Z. Так как в данной случае предельные полезности имеют вид:

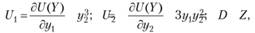
то необходимые условия оптимума (8.2) дают следующую систему уравнений (А - множитель Лагранжа):

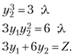
После подстановки первого уравнения во второе получим 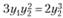. Выразив из третьего уравнения 3у, и подставив в последнее равенство, будем иметь 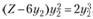, откуда можно получить, что 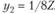. Подставив этот результат в третье уравнение, получим у₁ = 1/12Z. Таким образом, для данного примера функции спроса на товары у₁ и у₂ от дохода Z имеют вид:

y₁ = 1/12 Z; у₂ = 1/8 Z.

Однофакторные функции спроса от дохода широко применяются при анализе покупательского спроса. Соответствующие этим функциям кривые у_i= f_i(Z) называются кривыми Энгеля (по имени изучавшего их немецкого экономиста). Формы этих кривых для различных товаров могут быть различны. Если спрос на данный товар возрастает примерно пропорционально доходу, то функция будет линейной, как в рассмотренном выше примере. Такой характер имеет, например, спрос на одежду, фрукты и др. Кривая Энгеля для этого случая представлена на рис. 8.4, а.

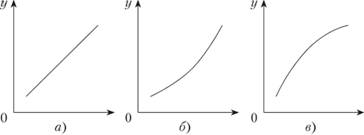
Рис. 8.4

Если по мере роста дохода спрос на данную группу товаров возрастает все более высокими темпами, то кривая Энгеля будет выпуклой (рис. 8.4, б). Так ведет себя спрос на предметы роскоши.

Если рост значений спроса, начиная с определенного момента, по мере насыщения спроса отстает от роста дохода, то кривая Энгеля имеет вид вогнутой кривой (рис. 8.4, в). Например, такой характер имеет спрос на товары первой необходимости.

Тот же принцип разграничения групп товаров по типам функций спроса от дохода использовал шведский экономист Л. Торнквист, который предложил специальные виды функции спроса (функции Торнквиста) для трех групп товаров: первой необходимости, второй необходимости, предметов роскоши.

Функция Торнквиста для товаров первой необходимости имеет вид

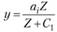
и отражает тот факт, что рост спроса на эти первоочередные товары с ростом дохода постепенно замедляется и имеет предел a₁ (кривая спроса асимптотически приближается к прямой линии у = a₁); график функции является вогнутой кривой I на рис. 8.5.

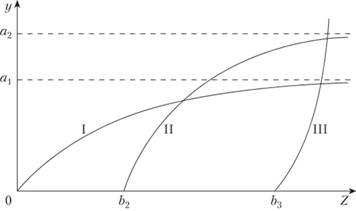
Рис. 8.5

Функция спроса по Торнквисту на товары второй необходимости выражается формулой

где

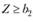
Эта функция также имеет предел а₂, но более высокого уровня; при этом спрос на эту группу товаров появляется лишь после того, как доход достигнет величины b₂, график функции - вогнутая кривая II на рис. 8.5.

Наконец, функция Торнквиста для предметов роскоши имеет вид

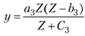, где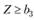

Эта функция не имеет предела. Спрос на эти товары возникает только после того, как доход превысит величину й₃ и далее быстро возрастает, так что график функции - выпуклая кривая III на рис. 8.5.

Кроме указанных функций, в аналитических моделях покупательского спроса используются также другие функции: степенные, S-образные и т.д.

Важную роль в анализе изменения спроса при небольших изменениях дохода играют коэффициенты эластичности. Коэффициент эластичности спроса от дохода показывает относительное изменение спроса при изменении дохода (при прочих не изменяющихся факторах). Вычисляется по формуле

(8.3)

где:

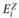- коэффициент эластичности для i-го товара (группы товаров) по доходу Z;

у_i- спрос на этот товар, являющийся функцией дохода:

у_i = f(Z)

Например, если спрос на товар описывается функцией Торнквиста для товаров первой необходимости, то формула (8.3) дает следующее выражение для коэффициента эластичности спроса от дохода:

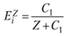
Во многих экономико-математических моделях эластичность функций относят к проценту прироста независимой переменной. Таким образом, коэффициент эластичности спроса от дохода показывает, на сколько процентов изменится спрос на товар при изменении дохода на 1%.

Коэффициенты эластичности спроса от дохода различны по величине для разных товаров, вплоть до отрицательных значений, когда с ростом доходов потребление уменьшается. Принято выделять четыре группы товаров в зависимости от коэффициента эластичности спроса на них от дохода:

- малоценные товары ( );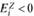

- товары с малой эластичностью ( );

- товары со средней эластичностью (E_i^Z близки к единице);

- товары с высокой эластичностью ( ).

К малоценным товарам, т.е. товарам с отрицательной эластичностью спроса от дохода, относятся такие, как хлеб, низкосортные товары. По результатам обследований, коэффициенты эластичности для основных продуктов питания находятся в интервале от 0,4 до 0,8, по одежде, тканям, обуви - в интервале от 1,1 до 1,3 и т.д. По мере увеличения дохода спрос перемещается с товаров первой и второй групп на товары третьей и четвертой групп, при этом потребление товаров первой группы по абсолютным размерам сокращается.

Перейдем к рассмотрению и анализу функций покупательского спроса от цен на товары. Из модели поведения потребителей (8.1) следует, что спрос на каждый товар в общем случае зависит от цен на все товары (вектора Р), однако построить функции общего вида y_i = φ(P) очень сложно. Поэтому в практических исследованиях ограничиваются построением и анализом функций спроса для отдельных товаров в зависимости от изменения цен на этот же товар или группу взаимозаменяемых товаров: y_i = φ(p_i).

Рассмотрим вопросы построения и использования в задачах оптимизации функций покупательского спроса от цены при неизменном доходе для конкретной группы товаров y_i = φ(p) более подробно. Основным критерием функционирования предприятий и фирм, производящих тот или иной товар, является прибыль. Сформулируем экономико-математическую модель на максимум прибыли при указанной форме зависимости спроса от цены. Конечную прибыль П можно представить в виде

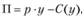(8.4)

где С(у) - совокупные затраты на производство и реализацию продукции; при этом предполагается, что объем выпускаемой продукции целиком совпадает с объемом спроса у, т.е. отсутствуют дефицит и затоваривание продукции.

Если известен вид функции спроса от цены y_i = φ(p), то, подставив эту функцию в (8.4), получим:

(8.5)

Тогда оптимизационная задача ставится следующим образом: определить значение цены р = р₀, при котором прибыль достигает своего максимума max П(р). В такой постановке эта задача решается классическими методами оптимизации. Вид функций φ(p) и С(φ(p)), а также их параметры могут быть определены методами математической статистики в результате обработки соответствующих статистических данных.

Рассмотрим случай, когда функция издержек С(у) является линейной и имеет вид

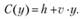(8.6)

Здесь h есть постоянная величина затрат, не зависящая от объема выпуска спроса продукции, т.е. h - это накладные расходы; величина v задает удельные затраты на единицу продукции. Будем считать, что зависимость спроса от цены также является линейной:

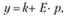(8.7)

где k характеризует максимально возможный объем спроса, а Е представляет собой некоторую условную эластичность спроса от цены; очевидно, что k > 0, а Е < 0.

Подставляя (8.6) и (8.7) в выражение для прибыли (8.5), будем иметь:

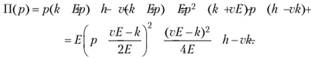(8.8)

С учетом того что Е < 0, можно сделать вывод о том, что максимум прибыли достигается при

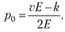(8.9)

и этот максимум равен

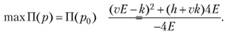(8.10)

График функции (8.8) представляет собой параболу, ветви которой направлены вниз. С учетом требования рентабельности выпуска продукции max П(р) > 0 этот график представлен на рис. 8.6.

Условием того, что эта рентабельность может быть достигнута, является условие положительности дискриминанта квадратного трехчлена от р (8.8):

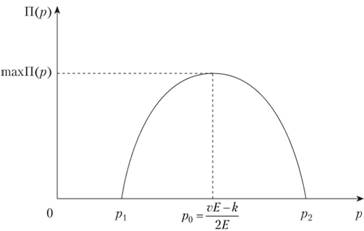
Рис. 8.6

Из этого неравенства следует, что

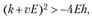
вследствие чего условие рентабельности можно записать в виде

(8.11)

С учетом (8.9) оптимальный объем выпуска продукции будет равен

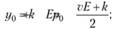(8.12)

в соответствии с этим требование рентабельности (8.11) может быть записано в виде

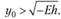(8.13)

Как видно из графика функции П(р) на рис. 8.6, существуют две "мертвые точки" р₁ и р₂, в которых прибыль равна нулю. Решение соответствующего уравнения дает для этих точек:

(8.14)

Таким образом, если установление оптимальной цены затруднено, то цена в любом случае должна лежать в интервале (p₁, p₂)> этим обеспечивается положительность величины прибыли от производства и реализации данного вида товара.

Пример 8.2. Рассмотрим числовой пример из области маркетинга книгоиздательства.

Пусть зависимость объема спроса на книжную продукцию от цены имеет вид (8.7), а функция издержек представлена в виде (8.6). Зададим следующие условные значения величин, участвующих в этих зависимостях:

- накладные расходы на производство и реализацию книжной продукции h = 36 тыс. руб.;

- удельные затраты на единицу (один экземпляр) этой продукции v = 20 руб./экз.;

- максимально возможный объем тиража k = 4000 экз.;

- условная эластичность спроса от цены Е = 40 экз./руб.

Тогда требование к объему тиража для обеспечения рентабельности определяется условием (8.13):

Оптимальная цена задается формулой (8.9):

Наиболее оптимальный объем тиража, обеспечивающий максимум прибыли, в соответствии с формулой (8.12) равен

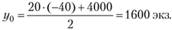
Интервал для цены, в пределах которого обеспечивается рентабельность данного издания, определяется выражением (8.14):

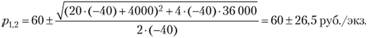
Таким образом, цена должна лежать в пределах от 33,5 до 86,5 руб. за один экземпляр; оптимальная цена равна 60 руб./экз.

Максимум прибыли, достигаемый при этом, рассчитывается в соответствии с формулой (8.10) и равен

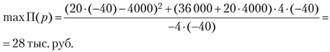
Представление зависимости спроса от цены в виде линейной функции (8.7) является весьма упрощенным, так как показатель эластичности спроса от цены здесь принимается равным постоянной величине Е. Более соответствует действительности предположение о зависимости коэффициента эластичности спроса от цены от величины самой цены. Проведенные конкретные исследования, учитывающие эту зависимость, позволяют с большой долей вероятности принять зависимость спроса у от цены р в виде одной из S-образных убывающих кривых, а именно в виде логистической кривой (функция Перла - Рида; см. параграф 5.1):

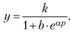(8.15)

График этой функции представлен на рис. 8.7; он имеет точку симметрии, совпадающую с точкой перегиба функции (8.15).

Тогда, предполагая зависимость затрат от спроса С(у) по-прежнему линейной в виде функции (8.6), получим выражение для прибыли:

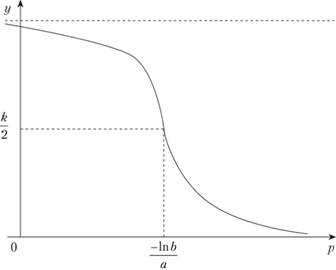
Рис. 8.7

(8.16)

Вычисляя производную этой функции по переменной р и приравнивая ее нулю, получим уравнение для нахождения критических точек:

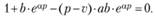
Разделив обе части этого уравнения на 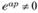, получим:

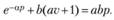(8.17)

Уравнение (8.17) имеет единственный корень р₀, так как кривые функций y = abp и у = е^-αр + b(av+1) имеют только одну точку пересечения (рис. 8.8). Трансцендентное уравнение (8.17) можно решить различными численными методами вычислительной математики. Решение этого уравнения р₀ можно оценить:

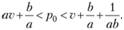(8.18)

Легко показать, что вторая производная функции прибыли от цены (8.16) в точке р = р₀ отрицательна; отсюда следует, что точка р₀ действительно является точкой максимума этой функции.

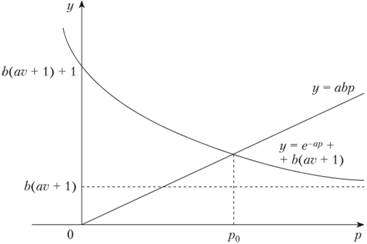
Рис. 8.8

Из соотношения (8.18) можно получить интервал для оптимального объема выпуска товара:

(8.19)

Положительные значения параметров а и b логистической кривой (8.15), если значение асимптоты k известно, определяются путем предварительного преобразования и логарифмирования, после чего на основе метода наименьших квадратов составляется и решается система нормальных уравнений относительно логарифмов параметров, а затем находятся и сами параметры. Если значение величины k (максимум выпуска) неизвестно, то для нахождения параметров k, а и b кривой (8.15) применяют приближенные методы: метод трех точек, метод трех сумм и др. Исходные данные для проведения указанных выше расчетов формируются на основе статистических наблюдений за процессом производства и реализации товарной продукции.

Для большинства товаров действует зависимость: чем выше цена, тем ниже спрос, и наоборот. Здесь также возможны разные типы зависимости и, следовательно, разные формы кривых. В практических задачах изучения спроса важно различать действительное увеличение спроса, когда сама кривая сдвигается вверх и вправо (происходит переход с кривой I на кривую II на рис. 8.9), и увеличение объема приобретаемых товаров в результате снижения цен при неизменной сумме затрат (переход от точки А к точке В по одной и той же кривой I на рис. 8.9). Как уже отмечено выше, в общем случае спрос на отдельный товар при прочих равных условиях зависит от уровня цен всех товаров. Относительное изменение объема спроса при изменении цены данного товара или цен других связанных с ним товаров характеризует коэффициент эластичности спроса от цен. Этот коэффициент эластичности удобно трактовать как величину изменения спроса в процентах при изменении цены на 1%.

Для спроса y_i на i-й товар относительно его собственной цены p_i коэффициент эластичности исчисляется по формуле

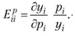(8.20)

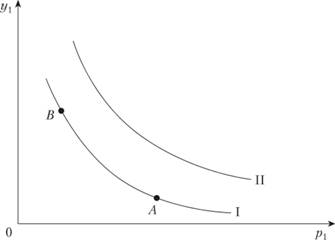
Рис. 8.9

Значения коэффициентов эластичности спроса от цен практически всегда отрицательны. Однако по абсолютным значениям этих коэффициентов товары могут существенно различаться друг от друга. Их можно разделить на три группы:

- товары с неэластичным спросом в отношении цены

- товары со средней эластичностью спроса от цены ( 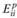близки к -1);

- товар с высокой эластичностью спроса ( ).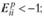

В товарах эластичного спроса повышение цены на 1% приводит к снижению спроса более чем на 1% и, наоборот, понижение цены на 1% приводит к росту покупок более чем на 1%. Если повышение цены на 1% влечет за собой понижение спроса менее чем на 1%, то говорят, что этот товар неэластичного спроса.

Рассмотрим влияние на спрос на какой-либо товар изменения цен на другие товары. Коэффициент, показывающий, на сколько процентов изменится спрос на данный товар при изменении на 1% цены на другой товар при условии, что другие цены и доходы покупателей остаются прежними, называется перекрестным коэффициентом эластичности. Для спроса у_i на i-й товар относительно цены p_j на j-й товар (i ≠ j) перекрестный коэффициент эластичности рассчитывается по формуле

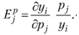(8.21)

По знаку перекрестных коэффициентов эластичности товары можно разделить на взаимозаменяемые и взаимодополняемые. Если , это означает, что i-й товар заменяет в потреблении товар j, т.е. на товар i переключается спрос при увеличении цены на товар j. Примером взаимозаменяемых товаров могут служить многие продукты питания.

Если 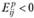, это служит признаком того, что i-й товар в процессе потребления дополняет товар ;, т.е. увеличение цены на товар j приводит к уменьшению спроса на товар i. В качестве примера можно привести такие взаимодополняемые товары, как автомобили и бензин.

В качестве иллюстрации в табл. 8.1 приведены значения прямых и перекрестных коэффициентов эластичности потребления от цен для одной из категорий семей. На основании этих данных по значениям прямых коэффициентов эластичности (по диагонали таблицы) можно сделать вывод, что продукты питания в целом мало эластичны по отношению к цене; одежда, ткани и обувь имеют среднюю эластичность; две последние группы товаров - товары с высокой эластичностью спроса по отношению к цене.

Таблица 8.1

Дата добавления: 2019-02-26; просмотров: 849; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!