II Оценка генеральной средней по выборочной средней
Пусть требуется изучить дискретную генеральную совокупность относительно количественного признака Х.
Генеральной средней х называется среднее арифметическое значений признака Х генеральной совокупности.
Далее под запись.
Интервальное оценивание неизвестных параметров ( Точность оценки, доверительная вероятность (надежность), доверительный интервал. Построение доверительных интервалов для оценки математического ожидания нормального распределения при известной и при неизвестной дисперсии. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределени.)
При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. Поэтому в таком случае лучше пользоваться интервальными оценками, то есть указывать интервал, в который с заданной вероятностью попадает истинное значение оцениваемого параметра. Разумеется, чем меньше длина этого интервала, тем точнее оценка параметра. Поэтому, если для оценки Θ* некоторого параметра Θ справедливо неравенство | Θ* - Θ | < δ, число δ > 0 характеризует точность оценки ( чем меньше δ, тем точнее оценка). Но статистические методы позволяют говорить только о том, что это неравенство выполняется с некоторой вероятностью.
Определение 1. Надежностью (доверительной вероятностью)оценки Θ* параметра Θ называется вероятность γ того, что выполняется неравенство | Θ* - Θ | < δ то есть
|
|
|
γ = p (| Θ* - Θ | < δ) или γ = p ( Θ * - δ < Θ < Θ * + δ ).
Таким образом, γ есть вероятность того,что Θ попадает в интервал ( Θ*- δ, Θ*+ δ).
Определение 2. Доверительным называется интервал, в который попадает неизвестный параметр с заданной надежностью γ.
При нахождении интервальных оценок решаются 3 основные задачи.
1) Дано: точность δ, объем n.
Найти: доверительную вероятность γ.
2) Дано: доверительная вероятность γ, объем n.
Найти: точность δ.
3) Дано: точность δ, доверительная вероятность γ.
Найти: объем n.
Рассмотрим построение доверительных интервалов для некоторых параметров распределений.
Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии.
Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим σ, и требуется по значению выборочного среднего 
оценить ее математическое ожидание а.
Будем рассматривать выборочное среднее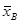 
как случайную величину 
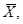а значения вариант выборки х1, х2,…, хп как одинаково распределенные независимые случайные величины Х1, Х2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ.
|
|
|
При этом М(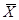 
) = а, 
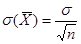(используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства 
.
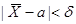Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:
р (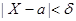 
) = 2Ф 
.
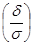Тогда , с учетом того, что
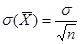, р ( 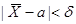) = 2Ф 
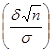==2Ф( t ), где 
.
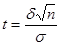Отсюда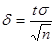 
, и предыдущее равенство можно переписать так:
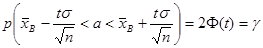. (1)
Итак, значение математического ожидания а с вероятностью (надежностью) γ попадает в интервал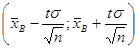 
, где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.
Пример. Найдем доверительный интервал для математического ожидания нормально распределенной случайной величины, если объем выборки п = 49,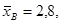 
σ = 1,4, а доверительная вероятность γ = 0,9.
Определим t, при котором Ф(t) = 0,9:2 = 0,45.Следовательно, t = 1,645. Тогда
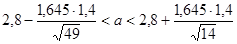, или 2,471 < a < 3,129.
Найден доверительный интервал, в который попадает а с надежностью 0,9.
Дата добавления: 2019-02-22; просмотров: 261; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!