ОПТИМИЗАЦИЯ ПРИМЕНЕНИЯ КОМПЕНСИРУЮЩИХ УСТАНОВОК В ГОРОДСКИХ СЕТЯХ

Постановка задачи

Причины компенсации реактивной мощности рассматривались ранее в п. 3.1 настоящей работы, основными из которых являются:

- возникновение дополнительных потерь активной мощности при протекании по сети реактивной;

- возникновение потерь реактивной мощности при протекании по сети реактивной;

- возникновение потерь напряжения.

Следствием увеличения потери мощности является уменьшение пропускной способности сети, в результате возникает необходимость применения в проектируемых электрических сетях элементов (кабельные и воздушные линии, трансформаторы и т.п.) с бо́льшей пропускной способностью или «усиления» существующей сети путём замены трансформаторов, оборудования распределительных устройств и т.п. Данные мероприятия сопровождаются значительными капитальными затратами.

Применение компенсирующих устройств позволяет уменьшить потери мощности и, следовательно, увеличить пропускную способность сети. Но установка компенсаторов реактивной мощности так же сопровождается капитальными затратами. В результате задача по компенсации реактивной мощности сводится к уменьшению потерь активной мощности с учётом минимальным капитальных затрат по установки компенсирующих устройств.

Далее в настоящей работе будут рассмотрены методы по определению мощности и мест установки устройств поперечной компенсации реактивной мощности с учётом минимизации денежных вложений и сроках окупаемости.

Численные методы

Градиентный метод с постоянным шагом

В основе данного метода лежит понятие о градиенте функции. Градиентом функции называется вектор, показывающий направление и величину максимальной скорости изменения функции в точке:

, (84)

где – единичные вектора (орты),

– частные производные функции по всем переменным.

Величина (модуль) вектора определяется как

. (85)

Сущность градиентного метода заключается в отыскании экстремума функции, т.е. точки, в которой , что говорит о том, что в этой точке функция не изменяется (не возрастает и не убывает).

Рисунок 5.2.1.1 – Иллюстрация градиентного метода с постоянным шагом

Рассмотрим градиентный метод с постоянным шагом на примере нахождения абсолютного минимума функции двух переменным Z( ). В большинстве случаях практического применения градиентного метода искомые переменных будут принимать положительные и нулевые значения. Соответственно область допустимых значений переменных будет определяться в первом квадранте системы координат x и y (рис. 5.2.1.1). В этой области произвольно выберем исходное приближение - и , которому соответствует значение функции . В соответствии с выражением (85) находится величина градиента функции в данной точке.

Затем выполняется первое приближение на шаг равный единице (λ=1) в сторону убывания функции, которому соответствует точка с координатами ( ). Значение целевой функции в этой точке составляет . Далее процедура приближения к искомому значению продолжается с постоянным шагом λ=1 до того, как относительное изменение целевой функции на предыдущем i-м и последующем (i+1)-м шагах оказывается меньше заданной точности вычислений ε:

. (86)

Рассмотренный выше градиентный метод с постоянным шагом достаточно прост, но основным его недостатком является большая вероятность определения значений в окрестностях минимума функции без его достижения (рис. 5.2.1.1). В результате приходится выбирать в качестве искомого решения одну из точек с координатами и .

Для нахождения более точного решения необходимо уменьшать длину шага приближения, что приводит к значительному увеличению вычислительных процедур на величину пропорциональную уменьшению шага.

Метод покоординатного спуска

Как и в градиентном методе с постоянным шагом выберем исходное приближение – точка с координатами ( ), соответствующая значению целевой функции . Далее вычисляем частные производные целевой функции и выбираем наибольшее по модулю значение производной. Пусть это будет производная . Следовательно, в направлении переменной функция имеет наибольшее изменение. «Если производная положительная, при увеличении переменной функция увеличивается. Если производная отрицательная, при увеличении переменной функция уменьшается» [10].

Далее изменяем значение переменной на один шаг в направлении уменьшения целевой функции. Производим данные операции до тех пор, пока значение целевой функции на, к примеру, втором приближении 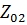не станет меньше значения целевой функции на третьем приближении . Исходя из этого следует, что экстремум функции находится в пределах значений 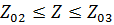при изменении значений переменной y. Затем возвращаемся к точке с координатами ( 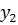) и производим «спуск» по переменной x. Вычисления производятся до того момента, пока целевая функция не начнёт увеличиваться, предположим .

Рисунок 5.2.2.1 – Иллюстрация метода покоординатного спуска

Процедура вычислений заканчивается, когда изменение любой переменной приводит к увеличению значения целевой функции, например это точка с координатами ( ).

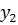Метод скорейшего «спуска»

В рассмотренных выше методах точность определения и количество операций зависят от шага приближения: чем величина шага больше, тем точность определения значения и количества вычислений меньше, а чем величина шага меньше, том точность и количество операций больше. В результате возникает необходимость в отыскании оптимального шага приближения, который позволял бы увеличить точность вычислений, но уменьшить количество расчётов. Одним из таких способов является метод скорейшего «спуска».

Алгоритм начала расчётов идентичен градиентному методу с постоянным шагом:

1. Принимается исходное приближение ;

2. Вычисляется значение целевой функции ;

3. По выражению (85) вычисляется значение .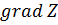

Из исходной точки в направлении убывания функции выполним два единичных шага (λ=1) и определим значение целевой функции в конце каждого шага и . По трём точка с координатами (0, ), (1, ) и (2, ) строится единичная парабола (рис. 5.2.3.1, б)

. (87)

Далее определим минимум данной параболы, продифференцировав функцию (87) по переменной λ и приравняв к нулю

, (88)

откуда .

Полученное значение является оптимальной длиной шага .

Рисунок 5.2.3.1 – Иллюстрация метода скорейшего спуска

Из исходной точке с координатами необходимо выполнить шаг длиной , результатом чего является первое приближение к искомому результату – точка с координатами . В данной точке вычисляем значение целевой функции . Далее процедура продолжается до достижения требуемой точности, определяемой из выражения (86).

Метод скорейшего «спуска» позволяет увеличить точность и уменьшить количество итераций, но объём вычислений на одном шаге больше.

Метод множителей Лагранжа

Ещё одним методом по решению задач поиска экстремума является метод множителей Лагранжа. Рассмотрим сущность данного метода.

Необходимо найти экстремум нелинейной функции

(89)

n переменных, при m ограничениях

(90)

Ограничения-неравенства в выражении (90) преобразуются в равенства, а свободные члены переносятся в левые части выражений. В результате получается система из m уравнений:

(91)

В соответствии с методом Лагранжа ищется абсолютный экстремум функции, имеющей следующий вид:

(92)

где – неопределённые множители Лагранжа.

Доказано, что относительный экстремум целевой функции (89) при ограничениях (91) совпадает с абсолютным экстремумом функции Лагранжа (92).

Поиск абсолютного экстремума сводится к определению частных производных и приравниванию их к нулю:

(93)

«Решение системы (93) даст координаты абсолютного минимума функции Лагранжа (92) или относительного минимума целевой функции (93) при ограничениях (91)» [10].

Применение численных методов

Используя численные методы, определим значения компенсирующих установок при условии минимизации потерь активной мощности и капитальных затрат на установку. В качестве примера используется магистральная схема, изображённая на рис. 5.3.1.

Рисунок 5.3.1 – Магистральная схема распределения реактивной мощности

Исходные данные:

- Напряжение U=10 кВ;

- Сопротивление линий R₁=4 Ом, R₂=6 Ом;

- Реактивная нагрузка: Q₁=300 кВАр, Q₂=500 кВАр;

- Удельные затраты на установку: z₀=0,5 у.е./кВАр;

- Удельные затраты на покрытие потерь: с₀=10 у.е./кВт.

Целевая функция представляет собой следующее выражение:

(94)

Для упрощения выражения (94) произведём следующие манипуляции: ; .

1) Определение мощности компенсирующих установок градиентным методом с постоянным шагом.

Определяются частные производные целевой функции по переменным и :

; (95)

. (96)

Определяются значения целевой функции (94) и частных производных при значениях мощностей компенсирующих устройств и :

;

Принимается длина постоянного шага равная λ=200 кВАр и, пользуясь выражением , определяется значения переменных:

Первое приближение: ; , ;

Второе приближение: , , .

Третье приближение: , , .

Четвёртое приближение: , , .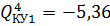

В связи с тем, что значение приняло отрицательное значение, дальнейшая итерация нецелесообразна. В качестве искомого значения принимается , , .

2) Определение мощности компенсирующих установок при использовании метода покоординатного спуска.

Определим частные производные по переменным и :

; (97)

. (98)

Определим значения целевой функции (94) и частных производных при значениях мощностей компенсирующих устройств и :

;

Так как , то целевая функция в направлении убывает быстрее. Соответственно, «спуск» начнём при изменении значения с величиной шага равной 200 кВАр.

Первое приближение: и . Значение целевой функции равно:

Второе приближение: и ;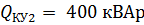

Третье приближение: и ;

В связи с тем, что значение целесообразности в увеличении переменной нет. Необходимо принять значение и производить аналогичные мероприятия в направлении другой переменной .

Второе приближение: , ;

Движение в направлении изменения значения нецелесообразно, т.к. .

Точка с координатами , находится в окрестностях минимума целевой функции Z=270 у.е.. Более точное значение невозможно получить в связи с принятым шагом.

При помощи программного обеспечения MS Exsel был получен следующий результат: ,

3) Определение мощности компенсирующих установок методом скорейшего спуска.

Как и в градиентном методе с постоянным шагом сначала принимаем исходное приближение , и вычисляем значение целевой функции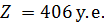

Определяются частные производные целевой функции по переменным и :

;

Для определения оптимального шага α используется выражение:

. (99)

Используя выражение (99) и значения частных производных с учётом начальных условий, получается , . Далее подставляются значения и 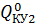в целевую функцию Z, для получения функции одной переменной

. (100)

Затем определяется первая производная по и приравнивается к нулю:

(101)

Соответственно 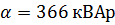и, пользуясь выражением , определяются значения переменных:

Первое приближение: ;

, ;

Второе приближение: , , .

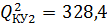Третье приближение: , , .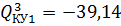

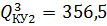В связи с тем, что значение приняло отрицательное значение, дальнейшее нахождение минимума нецелесообразно. В качестве искомого значения принимается , , .

4) Нахождение мощности компенсирующего устройства методом множителей Лагранжа

В исходных данных ограничения по мощности компенсирующих установок отсутствуют, соответственно, применение метода множителей Лагранжа в полном объёме невозможно. В связи с этим вводится допущение, что множитель Лагранжа λ=0, и определяются частные производные целевой функции (94), приравнивая их к нулю:

; (102)

(103)

Из выражения (102) выразим :

. (104)

В выражение (103) заменяется на выражение (104) и находится решение:

;

, а что соответствует значению целевой функции Z=243,75 у.е.

Так как значение мощности компенсирующей мощности не может меньше нуля, то искомым значением считается , , что соответствует значению целевой функции Z=286 у.е.

При помощи программного обеспечения MS Exsel при условии, что , , был получен следующий результат: ,

При сравнении выше применённых методов следует, что наиболее близким по минимальному значению целевой функции является результат вычислений при использовании метода покоординатного спуска ( , ).

В результате установки компенсирующих устройств эксплуатационные затраты уменьшились на 136 у.е. по сравнению с затратами без использования компенсирующих устройств (Z=406 у.е.).

Дата добавления: 2019-02-22; просмотров: 385; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 9 10 11 121314 Следующая ⇒

Мы поможем в написании ваших работ!