Выполним вычисления в среде Mathcad.

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Информационных технологий и телекоммуникаций

Коровина Л.И.

Методические указания к практическим занятиям

По дисциплине "Математическая экономика"

На практических занятиях и в самостоятельной работе над курсом студентам рекомендуется пользоваться нижеприведёнными методическими указаниями и практическими приёмами выполнения тех заданий, которые, как предполагается, должны выполняться с помощью электронных таблиц Microsoft Excel и пакетов Mathcad , Maple и Statistica в компьютерных классах ПК.

Предполагается, что все практические занятия проводятся в компьютерных классахи каждый студент работает за отдельным компьютером.

Результаты работы должны быть сохранены на отдельном носителе до зачёта или экзамена.

При защите каждой задачи студент должен проявить следующие знания и умения:

уметь формулировать постановку экономической задачи,

связно излагать процесс построение математической модели,

осознавать условия применимости математической модели,

грамотно анализировать полученные результаты,

правильно отвечать на контрольные вопросы о методах решения задачи и об используемых при этом информационных технологиях.

Занятие №1

Тема задания. Нелинейные уравнения в моделировании экономических процессов и методы их решения. (4 часа).

Содержание задания.

Аналитические и численные методы решения нелинейных уравнений. Решение нелинейных уравнений в пакетах Mathcad, Maple.

Задача 1.Постройте графики зависимости спроса от дохода для малоценных товаров D₀(x), товаров первой необходимости D₁(x), товаров второй необходимости D₂(x), и для предметов роскоши D₃(x), используя математическую модель, предложенную шведским ученым Торнквистом. Исследуйте также изменение вида кривых при изменении параметров α, β, γ.

Пусть α =15, β =5, γ=10.

D₀(x) = (α*х)* (x+β)/( х²+ γ) .

К какому предельному значению стремится спрос D₀(x) при неограниченном увеличении дохода x ?

D₁(x) = (α*х)/(x+β) .

Определите графически, при каких значениях дохода х значения спроса D₁(x) начинают отличаться от предельного значения меньше, чем на 3 ?

D₂(x) = [α *(х- γ)]/( x+ β) .

Определите графически, при каких значениях дохода х значения спроса D₂(x) превышают значение 12.

D₃(x) = [α*x* (х- γ)]/( x+ β) .

Существует ли предел возрастания спроса при увеличении дохода в этом случае?

(Можно рассмотреть также варианты заданий из задачи 3.19, стр.603 [2]).

Рекомендации к решению. Решение задачи 2 выполняется аналогично приведенному на стр. 211 - 213 учебника [2].

Определим исследуемые функции.

построения функций зададим, например, следующим образом: 0<x<100, 0<D<30.

Чтобы построить несколько графиков в одной и той же системе координат, вводите имена функций по оси ординат через запятую.

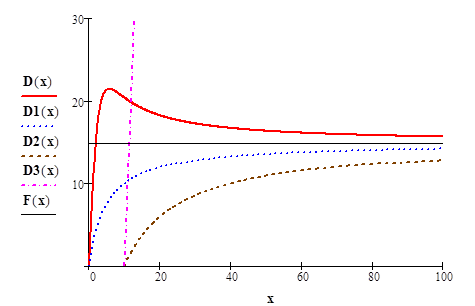
Проанализируем графики.

Спрос на малоценные товары растёт при малых доходах, затем достигает максимума и при дальнейшем увеличении дохода убывает, приближаясь асимптотически к величине сверху.

Спрос на товары первой необходимости растёт с ростом дохода, стремясь к величине a снизу.

Товары второй необходимости и предметы роскоши приобретаются только при доходах свыше g. Причем, спрос на товары второй необходимости ограничен сверху величиной a , а на товары роскоши растет неограниченно с ростом доходов.

Задача 1.2. Постройте график заданной функции спроса на малоценные товары в зависимости от дохода x : . Исследуйте вид кривой при разных значениях параметров , , .

Решение задачи.

Пусть вначале меняется при постоянных 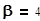, =5 Выполним присвоения в рабочей области и построим графики.

Теперь пусть меняется при постоянных , . Зададим присвоения в рабочей области.

Теперь пусть меняется при постоянных , b= 4 .

Зададим присвоения в рабочей области и построим графики.

Анализ графиков выполните самостоятельно.

Задача 2 . Постройте в среде Mathcad кривые спроса D(Q) = -AQ + B и предложения S(Q) = Q²/C + Q/d + E .

Найдите графически приближенно и затем численно с заданной точностью e=0.01 равновесную цену товара.

Исследуйте обусловленность вычислительной задачи..

Варианты значений констант A,B,C, d, E индивидуальных заданий можно взять из задачи 3.18, стр.603 [2] или задать по формулам:

A= (11*N)/(N+2) , где N - номер варианта,

B=110 , C=5 , d=3 , E=80.

Пример решения задачи при A=4 , B=120 , C=4 , d=2 , E=80.

Построим графики функций спроса и предложения, найдём количество товара Qравн, при котором достигается равновесная цена, и определим значение равновесной цены товара P.

Определяем в рабочей области функции и строим их графики.

A:=4 B:=120 C:=4 d:=2 E:=80.

1. Графическим способом найдём значения

Qравн=6.51 ; P=93.96

Для этого один раз щёлкните левой клавишей мыши (ЛМ) по области графика, появятся маркеры и подключится графический редактор. Кликните один раз правой клавишей мыши (ПМ) по области графика. Появится меню. Выберите команду trace. Подведите курсор в виде стрелки к точке пересечения кривых и щёлкните ЛМ. В диалоговом окне высветятся значения координат точки пересечения.

2. Уточним значения, найденные графическим способом,

с помощью вычислительного блока (Given...Find).

ОТВЕТ. Графическим способом найдены значения Q=6.51 ; P=93.96 .

Уточнённые данные: Q=6.52, P=93.90 ( все знаки верные).

Замечание. При решении задачи можно воспользоваться также рекомендованной литературой - стр. 210 - 211 учебника [2].

Указание. При исследовании обусловленности задачи варьируйте наименьший по модулю козффициент. Используйте относительные погрешности.

Занятие№2

Тема задания. Моделирование задач микроэкономики (4 часа).

Содержание задания.

Построение гравитационной модели поведения потребителя.

Вычисление для заданной функции спроса P(Q) эластичности Ed спроса по цене и соответствующего предельного дохода .

Текущий контроль.

Экспресс-опрос. Индивидуальная беседа с каждым из студентов по результатам выполненных заданий.

Задача 1.Постройте гравитационную модель поведения потребителя при наличии двух притягательных центров A и B, расположенных на расстоянии 2a друг от друга.

Замечание. Пояснения к математической модели.

Гравитационная модель У. Рэйли (ам. , 1929г.) используется для оценки предпочтений населения при выборе товаров, услуг, мест отдыха и так далее.

В основе её лежит принцип притягательности центров тяготения, аналог физической теории тяготения.

Согласно этому принципу, притяжение FAM, создаваемое центром A в точке M, обратно пропорционально квадрату расстояния между центром A и точкой M:

Аналогично, центр B , расположенный на расстоянии от точки B, создаёт в точке M притяжение

Здесь KA и KB -некоторые постоянные, характеризующие притягательность торговых центров A и B соответственно.

Интересно рассмотреть те точки, находясь в которых потребитель испытывает одинаковое притяжение со стороны обоих торговых центров.

Приравняем силы притяжения: FAM =FBM , то есть

Если ввести обозначение K=KA / KB , то получим условие "безразличия" в следующем виде

Решение задачи. Пусть расстояние между центрами притяжения равно 2a. Выберем декартову прямоугольную систему координат так, чтобы центры притяжения A и B располагались на оси абсцисс на одинаковом расстоянии от начала координат. Тогда координаты точек A и B будут соответственно (-a,0) и

(a,0) .Из условия "безразличия" получаем уравнение "линии безразличия" :

(x+a)^2 +y^2 = K*[(x-a)^2 + y^2].

Решим в среде Matcad это уравнение относительно y и построим графики найденных "линий безразличия". Убедимся, что получится окружность.

Решение уравнения найдём при следующих, например, значениях коэффициентов: a = 1 , K = 2 ( то есть расстояние между торговыми центрами равно 2 , и центр A в два раза притягательнее центра B).

Выполним вычисления в среде Mathcad.

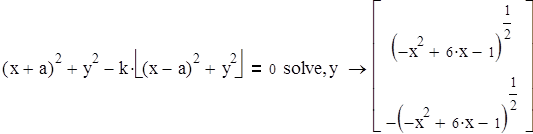
Присвоим имена каждому из решений:

Построим графики найденных "линий безразличия" ( масштабные единицы по осям выбираем однаковыми):

Легко видеть, что графики найденных "линий безразличия" образуют окружность.

Находясь в точках окружности, потребитель испытывает одинаковое притяжение со стороны обоих торговых центров. Если потребитель находится внутри окружности, то для него притяжение центра B будет больше, чем центра A., а если вне окружности, то для него более предпочтительным окажется центр A.

Посмотрим теперь, как изменится "линия безразличия" , если расстояние между центрами увеличится. Пусть, например будет a=3. Решим задачу.

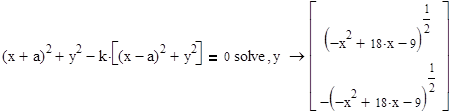
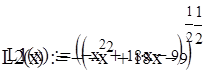
Радиус окружности увеличился, и она сместилась вправо.

Замечание. Выполнив несложные алгебраические преобразования, можно показать, что радиус окружности при K>1 равен

Решите далее аналогичную задачу по определению "линии безразличия" для Вашего номера варианта N, выбрав следующие значения коэффициентов:

a = 1 + 0.2*N, K = 2 + 0.1*N .

Задача 2.Найдите для заданной функции спроса P(Q)= -aQ^2+bQ+c эластичность Ed спроса по цене и соответствующей предельный доход R_p(Q). Постойте графики эластичности Ed (Q) и предельного дохода. Найдите значения Q и соответствующую цену, при которой модуль Ed равен единице.

Указания к решению задачи.

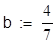В рабочей области документа Mathcad задаём значения констант и вычисляем эластичность.

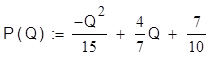Построим графики [-Ed(Q)], R_p(Q), F(Q) в зависимости от количества товара Q ( в стоимостных единицах).

Один раз щёлкните левой клавишей мыши (ЛМ) по области графика, появятся маркеры и подключится графический редактор. Ещё два щелчка ЛМ по области графика вызовут появление диалогового окна графического редактора. Отредактируйте графики.

В пакете Mathcad имеется возможность графически определить координаты точек графика. Для этого нужно щёлкнуть один раз по графику ЛМ, потом один раз правой клавишей мышы (ПМ) и выбрать в появившемся меню trace.

Появится новое диалоговое окно.

Если теперь подвести курсор-стрелку к точке пересечения графика функции [-Ed(Q)] и F(Q) и щёлкнуть ЛМ , то в диалоговом окне появятся координаты точки, на которую указывает курсор. Верхнее из чисел даёт

значение количества товара, при котором модуль эластичности равен единице.

Графически найдём значения координаты точки, где Ed =-1, а именно Q1=6.38

Для уточнения полученного значения обратимся к вычислительному блоку

Given

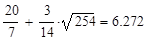
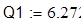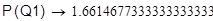
Графически найдено значение Q1, где модуль Ed равен 1, Q1=6.38 .

Уточненные данные: Q1=6.27, P(Q1)=1.66 .

Область эластичности спроса по цене: Q меньше чем 6.38

Точность вычислений определяется величиной погрешности вычислений в вычислительном блоке: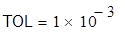

Замечание. Решение задачи выполняется аналогично приведенному на стр 218 - 220 учебника [2]. Варианты заданий можно взять из задания 3.22 на стр. 604 этого же учебника.

Занятие №3

Тема задания. Межотраслевой баланс. Модель Леонтьева.

Содержание задания. Построение модели межотраслевого баланса для четырёх отраслей экономики.

Решение задачи из учебника [2].

Текущий контроль.

Индивидуальная беседа с каждым из студентов по результатам задания 2, 3.

Задача 2. Постройте в среде Maple график и изокванты заданной производственной функции Q(K,L) = K^1/5L^4/5 . Дайте экономическую интерпретацию поведения графика функции и изоквант. Вычислите предельные продукты труда и капитала, и коэффициент заменяемости ресурсов.

(Варианты заданий можно взять из задачи 3.20, стр.603 [2]).

Постройте анимацию графика производственной функции.

Замечание. Решение данной задачи в среде Mathcad приведено на стр. 290 - 291 учебника [2].

Занятие№4

Тема задания. Моделирование динамических задач экономики.

Содержание задания. Динамические системы в экономических задачах.

Динамическая модель конкуренции. Уравнения Вольтерра - Лотка.

Определение доходов торгующих стран в сбалансированной системе международной торговли с заданной структурной матрицей торговли.

Задача 1. Рассмотрим один из самых известных примеров описания динамики взаимодействия конкурирующих популяций, а именно, уравнения Вольтерра - Лотка. Эта модель с успехом применяется для простейшего описания взаимодействия практически любых конкурирующих популяций, будь то животные или насекомые или рынки, банки, фирмы.

Предположим, что имеются две популяции - жертв и хищников.

Введём обозначения: x1(t) - количество жертв в момент времени t, x2(t) - количество хищников. Пусть коэффициент a есть относительная скорость размножения жертв в отсутствие хищников, (-bx2) - уменьшение этой скорости от потерь из-за хищников, коэффициент (-с) - относительная cкорость изменения числа хищников в отсутствие пищи, d - относительная cкорость изменения числа хищников в присутствии жертв в количестве x1(t) .

Тогда простейшей математической моделью динамической системы, описывающей изменение численности двух конкурирующих популяций во времени, является задача Коши для системы двух дифференциальных уравнений:

x1'=(a-b*x2)x1 , x2'=(-c+d*x1)x2

с начальными условиями: x1(t0)- начальное значение количества жертв, x2(t0)- хищников,

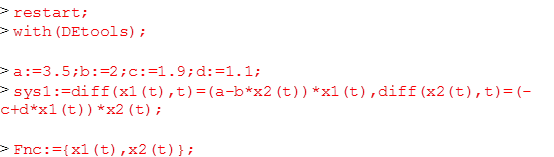
Найдём решение задачи, то есть функции x1(t) и x2(t) , при конкретном выборе постоянных, построим графики решения и фазовый портрет динамической системы в пакете Maple..

Найдём численное решение задачи методом Рунге-Кутта (установлен по умолчанию).

Проверим работу программы:

> F1(3);

В пакете расширенной графики plots построим графики решений.

Легко видеть, что решения имеют колебательный характер. При появлении хищников в начальный момент число жертв убывает. Число же хищников сначала растёт, достигает максимума, а затем из-за нехватки пищи начинает убывать. Графически можно определить, что когда число хищников убывает до 1.71 (при t=1.07) число жертв минимально, но затем популяция жертв начинает увеличиваться и достигает максимума. Число хищников также через некоторое время начинает расти и цикл повторяется.

Определите графически величину периода колебаний.

Построим далее трёхмерную траекторию движения. Воспользуйтесь, пожалуйста, возможностью повращать получающийся график с помощью левой клавиши мыши.

Построим далее фазовый портрет.

Фазовый портрет представляет собой замкнутую гладкую кривую (цикл), как и следовало ожидать для автономной системы дифференциальных уравнений.

Определите. пожалуйста, графически пределы изменения количества хищников и количества жертв.

Задача 2. Решите задачу макроэкономики определения доходов торгующих стран в сбалансированной системе международной торговли с заданной структурной матрицей торговли

Итак, рассмотрим линейную модель международной торговли.

Пусть структурная матрица торговли имеет следующий вид:

Требуется вычислить национальные доходы торгующих стран в сбалансированной системе международной торговли.

Решение задачи . Рассмотрим решение задачи в среде Mathcad.

Проверим, является ли матрица A структурной матрицей торговли в какой-либо сбалансированной системе международной торговли. Для этого вычислим суммы коэффициентов, стоящих в каждом столбце. Каждая сумма должна равняться единице (почему?).

Зададим нумерацию строк и столбцов матрицы A , начиная не с нуля, как установлено в Mathcad по умолчанию, а с единицы.

Выполняем суммирование:

Далее, вычислим собственный вектор матрицы A при собственном значении, равном единице.

Вначале получите справку о синтаксисе команды

>help(eigenvec);

Затем, решаем задачу.

Ответ. Для сохранения баланса в системе международной торговли национальные доходы четырёх торгующих стран должны удовлетворять условию

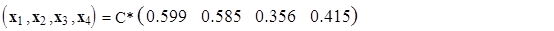где C - произвольная константа.

Занятие №5

Тема задания. Приближение таблично заданных функций. (2 часа)

Содержание задания.

Приближение таблично заданных экономических зависимостей. Прогнозирование в среде MAPLE результата деятельности торгового предприятия с помощью кубического сплайна и методом наименьших квадратов с целью выработки рекомендаций для лица, принимающего решение (ЛПР).

Задача 1. Решите задачу прогнозирования дохода торгового предприятия (в млн. руб.).

Решение задачи. Используя таблицу значений функции Y(X) найдём приближение этой функции кубическим сплайном. Построим график найденного сплайна. Вычислим значение кубического сплайна в точке X=15. Эти операции в среде MAPLE можно выполнить, например, нижеприведённым способом ( после каждого оператора следует нажать "Enter").

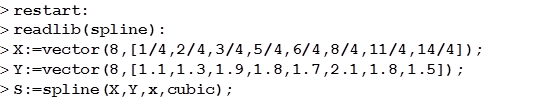
Здесь время задано в долях месяца.

На экране появится формула кубического сплайна.

Постройте график сплайна на отрезке [1/4,15/4] с помощью оператора > plot(S(x),x=1/4..15/4);

Далее вычислим прогнозируемое значение дохода предприятия на 15-ю неделю. Для этого запишем оператор:

куда вместо F(15/4) скопируем с экрана многочлен третьей степени, который определяет сплайн при значениях x , больших, чем 14/4, и подставим в него вместо x число 15/4.

Задача 2. Решите предыдущую задачу методом наименьших квадратов.

Рекомендация к решению задачи. Решение задачи можно выполнить аналогично решению следующей общей задачи наилучшего точечного среднеквадратичного приближения.

Постановка задачи. Пусть известны 10 значений функции Y=Y(X) с погрешностью E<=0.1 :

Y(1)=0.2, Y(1.1)= 1.7, Y(1.3)= 2.9, Y(1.4)=3.4, Y(1.5)= 3.6,

Y(1.6)=3.3, Y(1.7)=3.4, Y(1.8)=3.3, Y(1.9)=3.6, Y(2.2 )=6.1.

Требуется

1.Приблизить функцию Y=Y(X)

а) алгебраическим многочленом второй степени ,

б) алгебраическим многочленом третьей степени

используя метод наименьших квадратов, и оценить погрешность приближений.

2. Вычислить приближённо значение функции Y при X=2.3 .

Решение задачи.

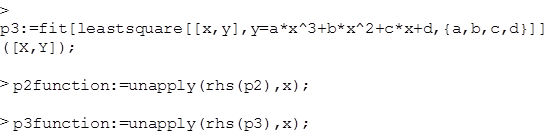
Оценим точность приближения. Вычислим величины E2 и E3 среднеквадратичных отклонений для найденных многочленов.

Поскольку погрешность приближения функции многочленом третьей степени совпадает в данном примере с погрешностью исходных данных, дальнейшее повышение степени приближающего многочлена нецелесообразно.

Вычислим прогнозируемое в точке X=2.3 значение функции Y=Y(X).

Построим графики найденных многочленов и соединим для наглядности ломаной линией исходные точки.

Ответ.

1. P2(x)=-0.5x^2 + 5.3x - 3.7

P3(x)=15.1x^3 - 73.1x^2 + 117.5x - 59.2

2. Приближённое значение функции Y(X) при x=2.3 равно 7.9 .

Дата добавления: 2019-02-13; просмотров: 800; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!