Равномерное движение по окружности.

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Пройденный путь S , перемещение dr, скорость v , тангенциальное и нормальное ускорение a_t, и a_n, представляют собой линейные величины. Для описания криволинейного движения наряду снимиможно пользоваться угловыми величинами.

Рассмотрим более подробно важный и часто встречаемый случай движения по окружности. В этом случае наряду с длиной дуги окружности движение можно характеризовать утлом поворота φ вокруг оси вращения. Величину

(1.15)

называют угловой скоростью. Угловая скорость представляет собой вектор, направление которого связывают с направлением оси вращения тела (рис.).

Обратим внимание на то, что, в то время как сам угол поворота φ является скаляром, бесконечно малый поворот dφ — векторная величина, направление которой определяется по правилу правой руки, или буравчика, и связано с осью вращения. Если вращение является равномерным, то ω=const и точка на окружности поворачивается на равные углы вокруг оси вращения за равные времена. Время, за которое она совершает полный оборот, т.е. поворачивается на угол 2π, называется периодом движения Т. Выражение (1.15) можно проинтегрировать в пределах от нуля до Т и получить угловую частоту

. (1.16)

Число оборотов в единицу времени есть величина, обратная периоду, — циклическая частота вращения

ν =1/ T . (1.17)

Нетрудно получить связь между угловой и линейной скоростью точки. При движении по окружности элемент дуги связан с бесконечно малым поворотом соотношением dS = R·dφ. Подставив его в (1.15), находим

v = ω r . (1.18)

Формула (1.18) связывает величины угловой и линейной скоростей. Соотношение, связывающее векторы ω и v , следует из рис. А именно, вектор линейной скорости представляет собой векторное произведение вектора угловой скорости и радиуса-вектора точки r:

. (1.19)

Таким образом, вектор угловой скорости направлен по оси вращения точки и определяется по правилу правой руки или буравчика.

Угловое ускорение — производная по времени от вектора угловой скорости ω (соответственно вторая производная по времени от угла поворота)

Выразим тангенциальное и нормальное ускорение через угловые скорости и ускорение. Используя связь (1.18),(1.12) и (1.13), получаем

a_t = β · R , a = ω ² · R . (1.20)

Таким образом, для полного ускорения имеем

. (1.21)

Величина β играет роль тангенциального ускорения: если β = 0.полное ускорение при вращении точки не равно нулю, a =R·ω² ≠ 0.

Связь линейных и угловых параметров.

При рассмотрении поступательного движения мат. точки мы рассмотрим линейные параметры:

S(перемещение)- расстояние от точки до конечной точки

v- скорость с которой двигаются тела

а- ускорение

Эти три величины связаны между собой : v = s’; a = v’=s’’

При рассмотрении вращательного движения мат. точки мы рассмотрим угловые параметры:

- угол отклонения

w- угловую скорость

E – угловое ускорение

Они так же связаны между собой : w = ‘; E = w’= ’’

В тоже время линейные параметры можно связать с угловыми параметрами:

R-радиус.

V= S= a_t = ·R, = ω ² ·R. a=

А именно, вектор линейной скорости представляет собой векторное произведение вектора угловой скорости и радиуса-вектора точки r:

Таким образом, вектор угловой скорости направлен по оси вращения точки и определяется по правилу правой руки или буравчика

Поступательное движение

Вращательное движение

Поступательное движение

Вращательное движение

Основной закон динамики

Работа и мощность

F∙Δt = mv₂ ‑ mv₁

M∙Δt = J∙ω₂‑ J∙ω₁

A=F∙s

A=М∙φ

F = m∙a

M = J∙ε

N = F∙v

N = M∙ω

Закон сохранения

Кинетическая энергия

момента импульса

импульса

V=V₀+at

r=r₀+V₀+

₀+

Законы Ньютона

Законы Ньютона образуют основу динамики — раздела механики, рассматривающего взаимодействие тел.

Первый закон Ньютона отражает свойство инерции, тел и часто называется законом инерции. Он утверждает, что всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Ясно, во-первых, что этот закон выполняется только в инерциальных системах отсчета. Во-вторых, отсюда следует важное заключение, что, поскольку изменение состояния покоя или равномерного движения связано с наличием в системе ускорения, последнее, в свою очередь, возникает как результат воздействия других тел. Это утверждение создает предпосылки для формулирования второго закона Ньютона.

Воздействие одного физического тела на другое характеризуется физической величиной, называемой силой. Сила, действующая на тело, сообщает ему ускорение. Величина полученного ускорения пропорциональна приложенной силе. Но разные тела под влиянием одинаковых сил приобретают разные ускорения. Данный опытный факт есть проявление уже упоминавшегося свойства инерции тела. Это свойство количественно характеризуется инертной массой тела — коэффициентом пропорциональности между приложенной к телу силой и полученным им ускорением.

Таким образом, второй закон Ньютона может быть записан в форме:

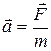где фигурируют вновь введенные физические величины: вектор силы F и инертная масса тела m. В таком виде его можно сформулировать следующим образом: ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе тела. Третий закон Ньютона имеет дело со взаимодействующими, телами.

F₁₂= F₂₁m₁a₁=-m₂a₂ F₁=-F₂

Он утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению. Важно подчеркнуть, что силы, о которых идет речь, приложены к разным взаимодействующим друг с другом телам.

Преобразования Галилея

Инерциальная система отсчета - такая система отсчета, в которой справедлив закон инерции: любое тело, на которое не действуют внешние силы, находится в состоянии покоя или равномерного прямолинейного движения.

Если наряду с выбранной инерциальной системой, рассмотреть другую, движущуюся относительно первой прямолинейно и равномерно, то свободное движение тела в новой системе будет также происходить с постоянной скоростью. Таким образом, существует бесконечное множество инерциальных систем отсчета. Во всех этих системах свойства пространства и времени одинаковы и одинаковы законы механики. Не существует никакой абсолютной системы отсчета, которую можно было бы предпочесть другим системам. В этом состоит принцип относительности Галилея. Его можно сформулировать и так: никакими механическими опытами невозможно установить, движется ли данная инерциальная система или покоится: оба состояния эквивалентны. Координаты точки в двух системах отсчета, одна из которых K' движется равномерно и прямолинейно относительно другой (K) со скоростью V, связаны соотношением (рис.)

При этом считается, что время абсолютно, т.е. течет одинаково в обеих системах: t' = t. Скорость точки в системе К связана со скоростью в системе К' формулой:

Математически принцип относительности Галилея можно сформулировать как требование инвариантности (неизменности) уравнений механики по отношению к преобразованию

Дата добавления: 2019-02-13; просмотров: 122; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!