Проверим правильность обращения
В случае, если нагрузка изменяется по гармоническому закону
(2.15)
то установившиеся колебания подчиняются тому же закону, то есть вектор динамических перемещений можно представить в таком виде:
(2.16)
Здесь: вектор амплитуд возмущающих сил -
(2.17)
вектор амплитуд вынужденных колебаний -
. (2.18)
В этом случае система уравнений (2.2) примет вид:
. (2.19)
Вводя обозначение
, (2.20)
запишем окончательно
(2.21)
Разрешая уравнение (2.21) относительно вектора амплитуд вынужденных колебаний, получим
(2.22)
Вектор динамических реакций определяется соотношением
(2.23)
Динамические моменты находятся из суммы произведений
(2.24)
где вектор единичных моментов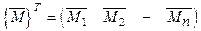 
в каждой из рассматриваемых характерных точек системы.
Очевидно, что полное напряженное состояние определится суммой динамических и статических моментов, перерезывающих и нормальных сил. Статические моменты можно найти из соотношения
(2.25)
|
|
|
где ускорение свободного падения - 
Здесь под статической нагрузкой подразумевается собственный вес оборудования, поэтому в выражении (2.25) учитываются моменты только от единичных сил, совпадающих по направлению с действием веса оборудования, образующего изгибающие моменты.
В случае действия на систему динамических нагрузок, изменяющихся по различным законам, будем представлять вектор динамических перемещений в виде разложения по собственным функциям (собственным формам колебаний)
(2.26)
где: неизвестная временная функция i – го тона колебаний - 
; нормированный вектор амплитуд собственных (свободных) колебаний i – го тона - 
.
Для анализа собственных колебаний удобно использовать соотношение (1):
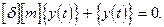(2.27)
При собственных колебаниях все части системы смещаются по одному и тому же закону, следовательно вектор перемещений можно представить в виде
(2.28)
где круговая частота собственных колебаний - 
Внося представление (2.28) в (2.27), приходим к выражению
(2.29)
Введем обозначения
|
|
|
(2.30)
где собственное число - 
Выражение (2.29) принимает вид:
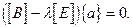(2.31)
Собственные числа находятся из соотношения
(2.32)
Процесс определения собственных чисел сводится к проблеме нахождения корней полинома, вытекающего из определителя
(2.33)
Собственные частоты определяются на основании второго равенства (2.30)
(2.34)
Собственные формы колебаний находятся с помощью соотношения
(2.35)
В силу линейной зависимости уравнений (2.35) возможно найти лишь отношения амплитуд. Если одну из них принять за единицу, то в результате будем иметь нормированный вектор (собственную форму) колебаний.
Внося представление (2.26) в выражение (2.2), получим:
(2.36)
Умножим почленно на транспонированную форму колебаний j-го тона
(2.37)
В силу ортогональности собственных функций
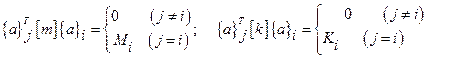(2.38)
|
|
|
Соотношение (2.37) принимает вид:
(2.39)
Здесь: приведенная масса 
приведенная жесткость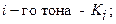 
приведенная нагрузка 
В результате приходим к “распавшейся” системе уравнений
(2.40)
где круговая частота собственных колебаний i-го тона
(2.41)
Частное решение уравнения (2.41)
(2.42)
легко находятся для любых законов изменения динамической нагрузки. Внося найденные 
в представление (2.26), определяем вектор динамических перемещений системы. Динамические реакции находятся из соотношения
(2.43)
Пример выполнения задания
Рис. Расчетная схема
Приложим единичные силы в направлении возможных перемещений масс и найдем эпюры изгибающих моментов
Рис. «Единичные» эпюры
Определим коэффициенты гибкости системы
Матрица 
получается путем перемножения матрицы гибкости на матрицу масс
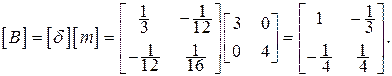
Уравнение для нахождения собственных значений имеет вид:
|
|
|
1. Устойчивость
Если при подборе сечений для растянутых элементов конструкции записывается условие прочности
(1.1)
то для сжатых элементов – условие устойчивости
(1.2)
Здесь: напряжения растяжения и сжатия соответственно - 
; расчетное сопротивление материала - 
; коэффициент снижения расчетного сопротивления при сжатии - 
.
Запишем уравнение равновесия для отсеченной части (сумма моментов относительно точки о)
(1.3)
С учетом известного соотношения
(1.4)
перепишем это уравнение
(1.5)
которое после введения обозначения
(1.6)
примет окончательный вид
(1.7)
Решение этого уравнения записывается так:
(1.8)
Удовлетворяем граничные условия
(1.9)
Из второго условия (9) следует, что
. (1.10)
Из (10) с учетом (6) вытекает формула Эйлера для критической силы шарнирно опертого стержня
(1.11)
Очевидно, что потеря устойчивости произойдет при n=1, то есть
(1.12)
Для произвольных граничных условий удобно ввести понятие приведенной длины
(1.13)
где коэффициент приведения длины - µ. В этом случае выражение для критической силы принимает вид:
(1.14)
Разделив (14) почленно на площадь сечения, приходим к выражению для критического напряжения
(1.15)
Здесь были использованы соотношения для радиуса инерции сечения - 
и гибкости стержня - 
При деформировании стали существуют две различных зависимости между напряжением и деформацией: линейная (закон Гука) и нелинейная (зоны текучести, упрочнения и разрушения). Граница между линейной и нелинейной зависимостью характеризуется напряжением пропорциональности, ей соответствует критическая гибкость - 
.
(1.16)
Из выражения (15) следует, что зависимость между критическим напряжением и гибкостью стержня описывается гиперболой и для малых гибкостей устремляется в бесконечность, что невозможно с физической точки зрения, т. к. напряжение в материале не может превышать его прочности. Следовательно, верхним значением напряжения при нулевой гибкости является предел прочности при сжатии - 
. На гиперболе существует точка с координатами С, соответствующая границе между линейным и нелинейным деформированием. Для критического напряжения между значениями 
Ясинским предложена квадратичная аппроксимация
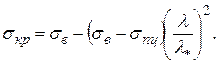(1.17)
Отношение критического напряжения к пределу прочности при сжатии названо коэффициентом снижения расчетного сопротивления при сжатии и обозначается буквой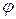 
.
(1.18)
Для зоны линейного деформирования сохраняется закон Гука, поэтому
(1.19)
Для отдельных конечных элементов целой конструкции неизвестны граничные условия, а значит и приведенные длины. Эта неопределенность обходится следующим образом: Производится расчет на устойчивость конструкции, из которого получается критическая сила, затем на основании (14) находится приведенная длина и все необходимые параметры для подбора сечения, удовлетворяющего условиям устойчивости.
(1.20)
Дата добавления: 2019-02-12; просмотров: 114; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!