Система с несколькими степенями свободы
Лекция
Динамика
Системы с одной степенью свободы
Рассмотрим действие переменной во времени силы 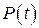 , действующей на груз с массой
, действующей на груз с массой 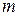 , расположенный на балке с изгибной жесткостью
, расположенный на балке с изгибной жесткостью  (массой балки пренебрегаем).
(массой балки пренебрегаем).

Рис. 1. Балка с расположенным на ней грузом, на который действует динамическая сила 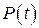
Мысленно отсечем груз и приложим к нему все действующие на него силы

Рис. 2. Силы, действующие на груз
Согласно принципу Д’Аламбера запишем уравнение равновесия для всех сил, действующих на груз (сумма проекций на ось y)
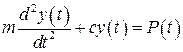 . (1.1)
. (1.1)
Деля на массу, получим каноническое уравнение для вынужденных колебаний системы с одной степенью свободы
 (1.2)
(1.2)
где круговая частота собственных (свободных) колебаний
 (1.3)
(1.3)
находится через жесткость  или через гибкость
или через гибкость  системы.
системы.
Период свободных колебаний связан с круговой частотой соотношением
 (1.4)
(1.4)

Рис. 3. Свободные колебания без учета диссипации энергии
Коэффициент гибкости для системы с одной степенью свободы с учетом упругих связей находятся с помощью соотношения:
 , (1.5)
, (1.5)
где  - изгибающий момент от единичной силы, приложенной в направлении колебаний массы;
- изгибающий момент от единичной силы, приложенной в направлении колебаний массы;  - символическая запись интеграла Мора-Максвелла;
- символическая запись интеграла Мора-Максвелла; 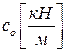 - линейная жесткость опоры;
- линейная жесткость опоры;  – моментная жесткость в системе;
– моментная жесткость в системе;  - реакция в упругой опоре;
- реакция в упругой опоре;  - момент в упругом шарнире.
- момент в упругом шарнире.
|
|
|
Характеристическое уравнение для однородного ( 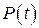 =0) уравнения (1.2)
=0) уравнения (1.2)
 (1.6)
(1.6)
имеет корни
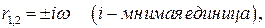 (1.7)
(1.7)
поэтому общее решение однородного уравнения (2.2) запишется так:
 (1.8)
(1.8)
Частное решение неоднородного уравнения для любого закона изменения нагрузки удобно решать способом вариации постоянных.

| .  . .
| ПЧ |
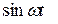
| 
| 0 |

| 
| 
|
Запишем определитель Вронского
 (1.9)
(1.9)
и его алгебраические дополнения при разложении по элементам последней строки
 (1.10)
(1.10)
Производные постоянных находятся из соотношений
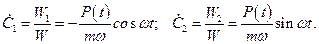 (1.11)
(1.11)
Общее решение неоднородного уравнения при произвольной нагрузке запишется так:
 (1.12)
(1.12)
Наиболее распространенной динамической нагрузкой является гармоническая нагрузка, которая появляется в результате вращения несбалансированных масс различных типов оборудования. В этом случае внешнее воздействие можно записать в виде
 (1.13)
(1.13)
|
|
|
с амплитудным значением возмущающей силы -  и круговой частотой -
и круговой частотой -  . Вынужденные колебания будут происходить с то же частотой, поскольку собственные колебания быстро затухают вследствие внутреннего трения в материале
. Вынужденные колебания будут происходить с то же частотой, поскольку собственные колебания быстро затухают вследствие внутреннего трения в материале
 (1.14)
(1.14)
где коэффициент динамичности
 (1.15)
(1.15)
Изгибающие моменты в системе находятся как сумма статической и динамической составляющей
 (1.16)
(1.16)
Из выражения (1.15) следует, что при совпадении частоты собственных колебаний и частоты возмущающей силы (явление резонанса) коэффициент динамичности равен бесконечности (рис. 5), то есть любая конструкция в этом случае обречена на разрушение.

Рис. 4. Коэффициент динамически без учета диссипации энергии
В действительности все конструкционные материалы обладают внутренним трением, которое приводит к затуханию собственных колебаний. Уравнение вынужденных колебаний с учетом диссипации энергии
 (1.17)
(1.17)
после деления на массу имеет вид:
 (1.18)
(1.18)
где 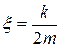 - относительный коэффициент демпфирования;
- относительный коэффициент демпфирования;  - частота собственных колебаний недемпфированной системы; с - жесткость, k - коэффициент демпфирования системы реагирует лишь на ускорение. Коэффициент затухания
- частота собственных колебаний недемпфированной системы; с - жесткость, k - коэффициент демпфирования системы реагирует лишь на ускорение. Коэффициент затухания 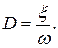 Характеристическое уравнение однородного уравнения (1.18)
Характеристическое уравнение однородного уравнения (1.18)
|
|
|
 (1.19)
(1.19)
имеет корни
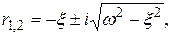 (1.20)
(1.20)
следовательно, решение будет иметь вид:
 (1.21)
(1.21)
или
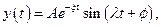 (1.22)
(1.22)
Амплитуды свободных колебаний уменьшаются по экспоненциальному закону.
Пусть внешнее воздействие изменяется по гармоническому закону  , а
, а  Тогда решение будет иметь вид, аналогичный (1.14)
Тогда решение будет иметь вид, аналогичный (1.14)

но коэффициент динамичности с учетом диссипации энергии запишется так
 (1.23)
(1.23)
Коэффициент динамичности с учетом диссипации энергии представлен на рис. 6. Кривые построены для нескольких значений относительного коэффициента затухания 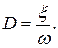

Рис. 5. Коэффициент динамичности демпфированной системы
(1 – D=1; 2 – D=0.5; 3 – D=0.25; 4 – D=0.1; 5 – D=0.05)
Последовательность решения задач:
1. Вычисляется коэффициент гибкости (податливости).
2. Определяется собственная частота.
|
|
|
3. Находится коэффициент динамичности.
4. Определяется динамическая реакция.
5. Определяются внутренние усилия от силы и веса оборудования.
Варианты заданий представлены на рис. 1-24.




Пример выполнения задания

Рис. 1. Система с одной степенью свободы
Для нахождения коэффициента гибкости приложим в направлении колебаний массы силу, равную единице (рис. 2) и построим эпюру изгибающих моментов М1. Коэффициент гибкости определяем по формуле

 .
.

Рис. 2. Единичная эпюра моментов
Круговая частота свободных колебаний

Коэффициент динамичности

Суммарный изгибающий момент состоит из статической составляющей (  ) и динамической реакции на действие возмущающей нагрузки (
) и динамической реакции на действие возмущающей нагрузки ( 

Учет статического действия массы здесь не производится, т. к. вес массы не создает изгибающего момента, а только сжимает стойку силой  . Эпюры изгибающего момента, поперечных и продольных усилий приведены на рис. 3.
. Эпюры изгибающего момента, поперечных и продольных усилий приведены на рис. 3.

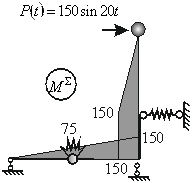

Рис. 3. Эпюры изгибающего момента, поперечных и продольных усилий
При отсутствии упругих связей коэффициент гибкости

Круговая частота свободных колебаний

Коэффициент динамичности

Суммарный изгибающий момент


Наличие демпфирующих элементов уменьшает динамические составляющие внутренних усилий в 11.325 раз.



Рис. 4. Эпюры изгибающего момента, поперечных и продольных усилий недемпфированной системы
Система с несколькими степенями свободы
Систему уравнений вынужденных колебаний системы с несколькими степенями свободы без учета диссипативных сил можно записать в матричном виде двояко: или
 , (2.1)
, (2.1)
или
 . (2.2)
. (2.2)
Здесь: вектор динамических перемещений
 ; (2.3)
; (2.3)
вектор ускорений
 ; (2.4)
; (2.4)
вектор динамических нагрузок
 ; (2.5)
; (2.5)
матрица масс
 ; (2.6)
; (2.6)
матрица гибкости (податливости)
 ; (2.7)
; (2.7)
матрица жесткости
 . (2.8)
. (2.8)
Элемент матрицы гибкости, стоящий на пересечении i-й строки и j-го столбца, можно найти из выражения
 (2.9)
(2.9)
Здесь: изгибная жесткость - 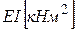 ; моменты от единичных сил, приложенных в направлении колебания i-й и j-й массы соответственно -
; моменты от единичных сил, приложенных в направлении колебания i-й и j-й массы соответственно -  (символическая запись
(символическая запись  означает взятие интеграла Мора-Максвелла или “перемножение” эпюр по способу Верещагина); жесткость линейной упругой связи -
означает взятие интеграла Мора-Максвелла или “перемножение” эпюр по способу Верещагина); жесткость линейной упругой связи -  ; реактивные усилия в линейной упругой связи от единичных сил, приложенных в i-ом и j-ом направлениях соответственно -
; реактивные усилия в линейной упругой связи от единичных сил, приложенных в i-ом и j-ом направлениях соответственно -  ; жесткость моментной упругой связи -
; жесткость моментной упругой связи - 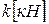 ; моменты в этой упругой связи от i-й и j-й единичных сил соответственно -
; моменты в этой упругой связи от i-й и j-й единичных сил соответственно - 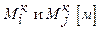 .
.
Пример 1. Найти матрицу гибкости (податливости)

Рис.1. К формированию матрицы гибкости

Таким образом, матрица гибкости имеет вид:
 .
.
Матрица жесткости 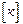 является обратной по отношению к матрице гибкости
является обратной по отношению к матрице гибкости
 , (2.10)
, (2.10)
следовательно, должно выполняться очевидное равенство
 , (2.11)
, (2.11)
где единичная матрица
 . (2.12)
. (2.12)
Элементы обратной матрицы находятся из соотношения
 , (2.13)
, (2.13)
где номер строки и столбца соответственно - i и j; определитель матрицы гибкости -  ; алгебраическое дополнение, получаемое путем разложения прямой матрицы
; алгебраическое дополнение, получаемое путем разложения прямой матрицы  по i-му элементу j-й строки -
по i-му элементу j-й строки - 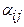 , т. е.
, т. е.

(2.14)
Пример 2. Найти матрицу  , обратную матрице
, обратную матрице  .
.
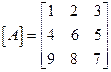 .
.
Определитель (детерминант) матрицы 
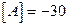 .
.
Алгебраические дополнения:
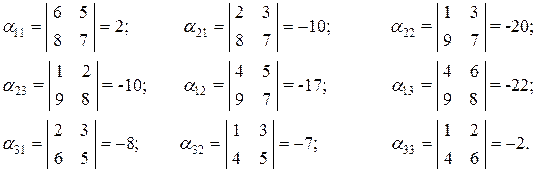
Элементы обратной матрицы 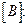
 Таким образом получена обратная матрица
Таким образом получена обратная матрица

Дата добавления: 2019-02-12; просмотров: 239; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
