Запись чисел в различных форматах

⇐ ПредыдущаяСтр 51 из 79Следующая ⇒

Шестнадцатеричный формат записи часто еще обозначают как HEX (hexadecimal ), двоичный – как BIN (binary ), а десятичный – как DEC (decimal ). Кроме этого, в ходу еще так называемый двоично‑десятичный формат – BCD (binary‑coded decimal ), о котором далее. Дело в том, что с помощью матричных шрифтов на компьютерах с текстовыми дисплеями воспроизводить индексы было невозможно, и вместо того, чтобы обозначать основания системы цифрой справа внизу, их стали обозначать буквами: «В» (или «Ь») – означает двоичную систему, «Н» (или «h») – шестнадцатеричную, отсутствие буквы означает десятичную систему:

13 = 00001101b = 0Dh.

Такая запись принята в языке ассемблера для процессоров Intel и стала общепринятой. Популярность языка С внесла в это дело некоторый разнобой: там десятичная система не обозначается никак, двоичная – буквой «Ь», а вот шестнадцатеричная – буквой «х», причем запись во всех случаях предваряется нулем (чтобы не путать запись числа с идентификаторами переменных, которые всегда начинаются с буквы):

13 = 0b00001101 = 0xD.

Такая запись также принята в ассемблере для микроконтроллеров AVR, который мы будем изучать далее. Запись ODh ассемблер AVR не «понимает», зато «понимает» представление НЕХ‑формата, принятое в языке Pascal: $0D. Обратите внимание, что запись в НЕХ‑формате обычно ведется в двухразрядном виде – даже если число имеет всего один значащий разряд, как в нашем случае, то в старшем пишется 0. То же самое относится и к двоичной записи, которая дополняется нулями до восьми разрядов. Таким образом подчеркивается, что речь идет о восьмиразрядных устройствах. А вот для десятичного представления ведущих нулей следует остерегаться – чтобы еще больше запутать пользователя, разработчики AVR‑ассемблера приняли для представления редко употребляемых восьмеричных чисел запись просто с ведущим нулем, без букв: например, 77 означает просто десятичное 77, а вот 077 будет означать 7·8 + 7 = 63₁₀.

Несколько слов о двоично‑десятичном формате BCD. Электронные устройства «заточены» под использование двоичных и родственных им систем счисления, потому что основой являются два состояния, т. е. двоичная цифра. Так что, соединив несколько устройств вместе с целью оперирования с многоразрядными числами, мы всегда будем получать именно двоичное число, и оперировать с ним оказывается значительно проще. Но для понимания человеком десятичный формат необходим – в десятичном виде числа приходится представлять всегда, когда речь идет о выводе, например, на цифровой дисплей. Для этой цели приходится преобразовывать двоичные/шестнадцатеричные числа в десятичные и хранить их в таких же байтовых регистрах или ячейках памяти.

Это можно делать двумя путями: в виде упакованного и неупакованного BCD. Неупакованный формат попросту означает, что мы тратим на каждую десятичную цифру не тетраду, как минимально необходимо, а целый байт. Зато при этом не возникает разночтений: 05h = 05₁₀, и никаких проблем. Однако ясно, что это крайне неэкономично – байтов требуется в два раза больше, а старший полубайт при этом все равно всегда ноль. Потому BCD‑числа при хранении и передаче по каналам связи всегда упаковывают, занимая и старший разряд второй десятичной цифрой, – скажем, число 59 при этом и запишется, как просто 59h. Однако 59h – это не 59! Ведь мы раньше установили, что записи 59h соответствует 5·16 + 9 = 89, что вообще ни в какие ворота не лезет.

Причина в том, что двоично‑десятичная запись числа не совпадает с шестнадцатеричной. Поэтому в общем случае перед проведением операций с упакованными BCD‑числами их распаковывают, перемещая старший разряд в отдельный байт и заменяя в обоих байтах старшие полубайты нулями. Иногда для проведения операций с BCD‑числами в микропроцессоре или микроконтроллере предусмотрены специальные команды, так что «вручную» заниматься упаковкой‑распаковкой не требуется. В качестве примера хранения чисел в упакованном BCD‑формате можно привести значения часов, минут и секунд в микросхемах энергонезависимых часов RTC (о них см. главу 22 ).

Немного двоичной арифметики

Правила двоичной арифметики значительно проще, чем десятичной, и включают две таблицы: сложения и умножения – несколько похожие на те же таблицы для логических переменных:

Как мы видим, правила обычного умножения одноразрядных двоичных величин совпадают с таковыми для логического умножения. Однако правила сложения отличаются, поскольку при сложении двух единиц результат равен 2, и появляется перенос в следующий разряд. Учитывая, что умножение многоразрядных чисел сводится к сложению отдельных произведений, там придется этот перенос учитывать (как это делается на практике, мы увидим в главе 15 ).

Сложности начинаются, когда мы хотим в двоичной системе представить отрицательные и дробные числа, причем не выходя за рамки двух знаков «ноль» и «единица», ибо в электронной схеме другие знаки представлять нечем.

Отрицательные двоичные числа

Самый простой метод представления отрицательных чисел – отвести один бит (логичнее всего – старший) для хранения знака. По причинам, которые вы поймете далее, значение 1 в этом бите означает знак «минус», а 0 – знак «плюс». Что произойдет с нашим числом при таком представлении?

В области положительных чисел не произойдет ничего, кроме того, что их диапазон сократится вдвое, – например, для числа в байтовом представлении вместо диапазона 0…255 мы получим всего лишь 0…127 (0000 0000–0111 1111). А отрицательные числа будут иметь тот же диапазон, только старший бит у них будет равен 1. Все просто, не правда ли?

Нет, неправда. Такое представление отрицательных чисел совершенно не соответствует обычной числовой оси, на которой влево от нуля идет минус единица, а затем числа по абсолютной величине увеличиваются. Здесь же мы получаем, во‑первых, два разных нуля («обычный» 0000 0000 и «отрицательный» 1000 0000), во‑вторых, оси отрицательных и положительных чисел никак не стыкуются, и производство арифметических операций превратится в головоломку. Поэтому поступим так: договоримся, что ‑1 соответствует число 255 (1111 1111), – 2 – число 254 (1111 1110) и т. д. вниз до 128 (1000 0000), которое будет соответствовать ‑128 (и общий диапазон всех чисел получится от ‑128 до 127). Очевидно, что если вы при таком представлении хотите получить отрицательное число в обычном виде, то надо из значения числа (например, 240) вычесть максимальное значение диапазона (255) плюс 1 (256). Если отбросить знак, то результат такого вычитания (16 в данном случае) называется еще дополнением до 2 для исходного числа (а само исходное число 240 – дополнением до 2 для 16). Название «дополнение до 2» используется независимо от разрядности числа, потому что верхней границей всегда служит степень двойки (в десятичной системе аналогичная операция называется «дополнение до 10»).

Что произойдет в такой системе, если вычесть, например, 2 из 1? Запишем это действие в двоичной системе обычным столбиком:

В первом разряде результата мы без проблем получаем 1, а уже для второго нам придется занимать 1 из старших, которые сплошь нули, поэтому представим себе, что у нас будто бы есть девятый разряд, равный 1, из которого заем в конечном итоге и происходит:

На самом деле девятиразрядное число 1 0000 0000 есть не что иное, как 256, т. е. то же самое максимальное значение плюс 1, и мы здесь выполнили две операции: прибавили к уменьшаемому эти самые 256, а затем выполнили вычитание, но уже в положительной области для всех участвующих чисел.

А что результат? Он будет равен 255, т. е. тому самому числу, которое, как мы договорились, и представляет – 1. Получается, что вычитание в такой системе происходит автоматически правильно, независимо от знака участвующих чисел. Если хотите, можете потренироваться и проверить, скажем, что будет, если в этой системе вычесть 240 из 100.

Немного смущает только эта самая операция нахождения дополнения до 2, точнее, в данном случае, до 256 – как ее осуществить на практике, если схема всего имеет 8 разрядов? В дальнейшем мы увидим, что иногда ее осуществлять вовсе не надо – некоторые электронные схемы ведут себя так, что при осуществлении вычитания вся процедура осуществляется автоматически. Особенно наглядно это выглядит для двоичных реверсивных счетчиков, которые мы будем рассматривать в главе 16 .

В точности так же ведут себя и соответствующие команды в микропроцессорах – и если вы захотите произвести операцию вычитания числа 2 из содержимого восьмибитового регистра, содержащего число 1, то в регистре окажется число 255 (все единицы). А интерпретация результата – как отрицательного числа или как положительного – это уже ваши трудности.

В микропроцессорах есть обычно и команда, которая возвращает дополнение до 2, в большинстве ассемблеров она называется NEG, от слова «негативный», потому что меняет знак, если мы договариваемся считать числа «со знаком». А как ее можно было бы осуществить «вручную», не обращаясь в действительности к 9‑му разряду? Вернемся к рассмотренным ранее примерам и выпишем столбиком исходные числа, результаты операции нахождения дополнения до 2 и результат еще одной манипуляции, которая представляет собой вычитание единицы из дополнения до 2, т. е., что то же самое, просто вычитания исходного числа из наивысшего числа диапазона (255):

Если мы сравним двоичные представления в верхней и нижней строках, то увидим, что они могут быть получены друг из друга путем инверсии каждого из битов. Эта операция называется нахождением дополнения до 1 (потому что число, из которого вычитается, содержит все 1 во всех разрядах; для десятичной системы аналогичная операция называется дополнение до 9 ). Для нахождения дополнения до 1 девятый разряд не требуется, да и схему можно построить так, чтобы никаких вычитаний не производить, а просто переворачивать биты. То есть, для полного сведения вычитания к сложению надо проделать три операции:

1. Найти дополнение до 1 для вычитаемого (инвертировать его биты).

2. Прибавить к результату 1, чтобы найти дополнение до 2.

3. Сложить уменьшаемое и дополнение до 2 для вычитаемого.

Заметим, что все сложности с этими многочисленными дополнениями связаны с наличием нуля в ряду натуральных чисел – если бы его не было, дополнение было бы всего одно, и операция вычитания упростилась. Так может, греки все же были в чем‑то правы?

В заключение обратим внимание на еще одно замечательное свойство двоичных чисел, которое часто позволяет значительно облегчить операции умножения и деления, а именно: умножению на 2 соответствует операция сдвига всех разрядов числа на один разряд влево, а операции деления на 2 – вправо. Крайние разряды (старший при умножении и младший при делении) в общем случае при этом должны теряться, но в микропроцессорах есть специальный бит переноса, в который эти «потерянные» разряды помещаются. Противоположные крайние разряды (младший при умножении и старший при делении) в общем случае замещаются нулями, но могут и замещаться значением бита переноса, что позволяет без лишних проблем делить и умножать числа с разрядностью больше одного байта. Как можно догадаться, умножению и делению на более высокие степени двойки будет соответствовать операция сдвига в нужную сторону на иное (равное степени) число разрядов.

Излишне говорить, что операцию сдвига разрядов в электронных схемах производить неизмеримо проще, чем операции деления и умножения. Есть и специальные схемы для этой операции – сдвиговые регистры, которые мы также будем «проходить» (в главе 16 ).

Дробные числа

Сразу заметим, что в некомпьютерной электронике дробными числами стараются не пользоваться. При необходимости их переводят в целые, умножая на соответствующую степень десяти (а чаще – даже на степень 2, что проще), при этом все остальные участвующие в расчетах величины также масштабируются в нужное число раз. Затем при выводе, к примеру, на цифровой дисплей, запятая просто устанавливается в нужном месте (иногда заранее, и без возможности изменения ее положения). То есть, для цифровой схемы не существует значения температуры, равного 30,81 градуса, а есть число 3081 в BCD‑формате. Примерно те же действия мы производили, когда конструировали цифровой термометр в главе 13 , – на самом деле он показывает целое число милливольт в нужном масштабе.

И все же – как мы можем при необходимости представить дробные числа, если двоичные разряды ничего о таковых «не знают» и могут воспроизводить только целые числа в соответствии с формулой (4)? Мы не будем рассматривать расширение этой формулы, включающее в себя представление в позиционной системе не только целых, но и всех действительных чисел «с плавающей запятой», т. к. в электронике такой вариант не хождения не имеет. В электронике и компьютерной технике используют другой способ представления действительных чисел – с помощью мантиссы и порядка, в так называемом нормализованном виде . При этом место запятой фиксируется:

0,0125 = 0,125·10^‑1,

1254,81 =0,125481·10⁴.

Разумеется, в электронных схемах все это лучше делать в двоичной форме, записывая порядок, как степень двух (скажем, операция выравнивания порядков при сложении таких чисел сведется просто к сдвигу мантиссы, как мы видели ранее).

Легко заметить, что и саму запятую, и основание степени тут можно опустить, записывая в память лишь мантиссу и порядок – конечно, если всегда помнить, что мы имеем в виду. Например, можно сделать так: отвести в памяти три байта, из которых первые два хранят цифры мантиссы, а третий отведен под порядок. Легко также подсчитать, каков будет диапазон чисел, могущих быть представленными таким образом, – число, которое представляет мантиссу, будет укладываться в диапазон от ‑32768 до 32767, т. е. иметь от 4 до 5 значащих десятичных цифр. На практике операции с дробными числами можно производить несколько проще, и мы будем их осваивать в главе 20 .

Коды, шифры и дешифраторы

По необходимости кратко коснемся темы кодирования и связанной с ней темы шифрования. Слово «код» (особенно в сочетании двоичный код) вы будете встречать очень часто, и следует понимать, что именно подразумевается под этим понятием в том или ином случае. Кроме того, сразу забежим немного вперед и покажем, как обращаться с реальными схемами на этом примере.

Код в общем случае – это совокупность правил (т. е. алгоритм) для представления информации в какой‑либо форме. Процесс применения к информационному сообщению этих правил называется кодированием , при этом полученная группа знаков или сигналов также называется кодом . Обратная операция – восстановление сообщения по известному коду – носит название декодирования . Например, код Морзе позволяет записать с помощью двух знаков – точки и тире – любую букву или цифру. Закодированное таким образом сообщение можно передавать с высокой надежностью в различных средах, характеризующихся высоким уровнем помех (в виде звуковых сигналов, в том числе по радио, в виде вспышек света разной длительности, перестукиванием через стены и т. п.).

Понятие кода применимо к формам представления информации лишь в тех случаях, когда между содержанием сообщения и его представлением в какой‑либо форме существует взаимно‑однозначное соответствие, т. е. по данной записи смысл сообщения может быть восстановлен единственным образом (если не считать возможных искажений при передаче). В этом смысле понятие кода может быть лишь ограниченно применимо, например, к письменной или устной речи, для которых характерна многозначность смысловых единиц. В гуманитарных дисциплинах, как правило, понятие кода используется в качестве метафоры (например, «смысловой код произведения искусства»).

Понятие кода нашло наиболее широкое применение для представления информации в цифровой форме. Самым распространенным цифровым кодом является двоичный код (т. е. представление любого знака или числа в виде набора двоичных цифр 0 и 1). Двоичный код, в свою очередь, служит основой для различных кодов, представляющих конкретные разновидности информации. В информатике часто также говорят про исходный код программ , что означает текст программы, записанный на одном из языков программирования.

На рис. 14.6 приведены различные стандартные коды для первых девяти букв латинского алфавита. Следует отметить, что азбука Брайля – система письменности для слепых (где жирная точка соответствует наличию выпуклости, а «худая» – ее отсутствию) – в полной мере является двоичным кодом, мало того, из принципа ее построения было многое заимствовано в современных системах компьютерных кодировок. А вот код Морзе, хотя и состоит из точек и тире, двоичным кодом не является: в нем используется как минимум еще один знак – пауза. Зато код Морзе намного экономичнее обычных двоичных кодов, таких, как ASCII, поскольку имеет переменное число точек‑тире для каждого символа, и часто встречающиеся буквы в нем короче, чем редко встречающиеся.

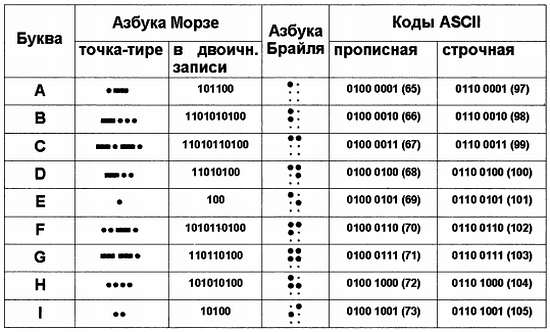
Рис. 14.6. Некоторые коды первых латинских букв

_{Для кодировки ASCII в скобках дано десятичное значение}

Понятие шифра, строго говоря, к электронике не относится. Шифр – это просто код, построенный специальным образом для обеспечения секретности при передаче сообщений, и занимается этим довольно сложная математическая дисциплина – криптография. Тем не менее, в электронике довольно часто употребляют наименование «дешифраторы» – для обозначения элементов, которые предназначены для преобразования одной разновидности кода в другую.

Типичным примером может служить микросхема К561ИД5 (рис. 14.7, а ), которая преобразует двоично‑десятичное число, подаваемое на входы X , в специальный код для управления семисегментными индикаторами. Сам такой индикатор вместе с таблицей его состояний представлен на рис. 14.8. В этой таблице в колонке под заголовком «BIN» представлены двоичные числа, соответствующие входам X дешифраторов на рис. 14.7.

Рис. 14.7 . Разводка выводов дешифраторов К561ИД5 (а) и 514ИД1/514ИД2 (б)

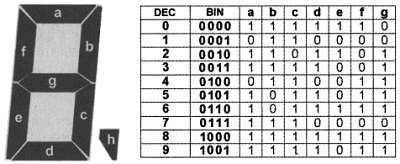
Рис. 14.8. Обозначения сегментов и таблица состояний семисегментного индикатора

Отметим, что К561ИД5 «заточена» под управление ЖК‑дисплеями, и потому имеет двухполярное питание и содержит отдельный вход F , на который подаются прямоугольные импульсы частотой несколько десятков герц (иначе, как мы знаем из главы 7 , сегмент ЖК‑индикатора будет засвечен навсегда). Сигнал на входе Е «защелкивает» выход – если на нем логический ноль (напряжение «земли»), то коды на выходе не будут меняться независимо от состояния входов, в нормальном состоянии там должна быть логическая единица (напряжение питания).

Если нужно управлять светодиодными индикаторами, для которых двухполярное пульсирующее питание не требуется, то выходы отрицательного питания и «земли» объединяют и на вход F подают напряжение «земли» (логического нуля). По выходам a‑f при этом приходится ставить дополнительные ключевые транзисторы или эмиттерные повторители для управления сегментами индикаторов, т. к. выходной ток микросхем серии 561 для непосредственного управления светодиодами недостаточен.

Микросхема К561ИД5 основана на так называемой технологии КМОП . А специально предназначенные для управления светодиодными индикаторами дешифраторы 514ИД1 и 514ИД2 (рис. 14.7, б ) основаны на технологии ТТЛ и потому ограничены одним напряжением питания (максимум 5,5 В), зато выходы у них намного мощнее (подробнее о технологиях логических микросхем и их электрических характеристиках мы узнаем из главы 15 ).

Различаются 514ИД1 и 514ИД2 полярностью выхода – у первого наружу выведен эмиттер выходного транзистора, коммутирующий ток через сегмент на «землю», а у второго – на выходе открытый коллектор. Таким образом, 514ИД1 предназначена для управления сегментными индикаторами с общим катодом, который подсоединяется к «земле», а 514ИД2 – индикаторами с общим анодом, который подсоединяется к питанию. Другое отличие – у 514ИД1 имеются встроенные токоограничивающие резисторы номиналом приблизительно 1 кОм, т. е. при падении напряжения на сегменте примерно 1,8–2 В (стандартном для красного светодиода) выходной ток будет составлять около 3 мА.

У 514ИД2 таких резисторов не имеется, и их приходится ставить дополнительно, непосредственно к выходу дешифратора индикатор присоединять нельзя. Зато здесь можно гибко управлять яркостью свечения в зависимости от индивидуальных характеристик индикаторов – зеленые и желтые индикаторы при одинаковом токе имеют большее падение напряжения, чем красные (номинально 2,4 В против 1,8 В), и могут светиться тусклее. При токе через сегмент около 5–6 мА сопротивление токоограничивающего резистора должно быть в пределах 360–510 Ом. Большими по размеру индикаторами, где прямое падение напряжения на сегменте удвоенное, с помощью этих микросхем приходится управлять также через внешние ключи, подключенные к более высокому напряжению.

При подаче напряжения «земли» на вывод «Г » этих микросхем все сегменты оказываются погашенными. Это позволяет осуществлять динамическую индикацию – управление многоразрядными индикаторами, при котором в каждый момент времени светится только один десятичный разряд. В результате удается сэкономить на количестве соединений (одноименные сегменты всех разрядов соединяются параллельно) и отчасти на потреблении схемы. Формально говоря, ток через каждый разряд при таком подключении должен увеличиваться пропорционально числу разрядов, чтобы сохранить ту же яркость – например, при четырех разрядах ток должен быть в четыре раза больше, т. к. каждый разряд горит лишь четвертую часть времени (но не забудьте, что у 514ИД2 есть предельное значение – 22 мА). Однако опыт показывает, что пропорциональное увеличение тока необязательно, визуально яркость сохраняется и при меньших значениях мгновенного тока через сегмент, что и позволяет немного сэкономить на питании. Более подробно мы будем говорить о динамической индикации при изучении микроконтроллеров, с помощью которых организовать ее гораздо проще и удобнее, чем с помощью обычных микросхем.

ГЛАВА 15

Дата добавления: 2019-02-12; просмотров: 389; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 46 47 48 49 505152 53 54 55 Следующая ⇒

Мы поможем в написании ваших работ!