Регрессия и метод наименьших квадратов
Все сказанное относилось к случаю, когда мы измеряем одну величину, имеющую некоторую случайную погрешность. Однако на практике нам часто требуется по экспериментальным данным получить оценку некоторой функции у (х ) – фактически это задача построения кривой по результатам опытных данных, которую вам, несомненно, приходилось не раз решать, если вы обучались в техническом вузе.
Процесс проведения кривой через какие‑либо точки (расчетные или экспериментальные) в общем случае называется аппроксимацией . Аппроксимацию следует отличать от интерполяции (когда по совокупности имеющихся значений функции и переменных рассчитывают значение функции в некоторой точке между ними) и экстраполяции (когда рассчитывают значения функции вне области, охваченной имеющимися значениями, в предположении, что там кривая ведет себя так же). Насчет последней операции следует отметить, что полиномы, полученные регрессионным способом (см. далее), за исключением разве что прямой линии, обычно для проведения экстраполяции не годятся – т. к. не несут в себе физического смысла и вне экспериментальной области могут очень сильно расходиться с реальной картиной.
Провести кривую, аппроксимирующую опытные данные, можно от руки на миллиметровке, но как решать такую задачу «правильно»? Причем, как и в предыдущем случае, желательно бы иметь возможность оценить погрешности измерений.
|
|
|
Принцип такого построения при наличии случайных ошибок измерения иллюстрирует рис. 13.7.

Рис. 13.7. Проведение аппроксимирующей прямой по экспериментальным данным
Разумно было бы проводить кривую (в данном случае – прямую) так, чтобы отклонения Δуi ,‑ были бы минимальными в каждой точке. Однако просто минимизировать сумму отклонений не получится – они имеют разный знак, и минимум получился бы при очень больших отрицательных отклонениях. Можно минимизировать сумму абсолютных значений отклонений, однако это неудобно по ряду чисто математических причин, потому используют уже знакомую нам сумму квадратов отклонений, – только ранее это было отклонение от среднего арифметического одной величины х , а теперь это отклонение опытных данных от кривой у (х ):
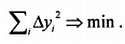
Такой метод называется методом наименьших квадратов .
Кстати, а какую именно кривую выбрать? Ведь кривые бывают разные: прямая, парабола, экспонента, синусоида… Опыт показывает, что на практике можно ограничиться полиномом, соответствующим разложению функции в ряд Тейлора (в математике доказывается, что любую другую непрерывную функцию всегда можно представить в виде такого ряда):
|
|
|
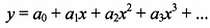
(5)
Это уравнение называется уравнением регрессии . Отметим, что здесь мы рассматриваем наипростейший случай – зависимость у от одного параметра x . В общем случае независимых переменных может быть несколько, но для наших целей простейшего случая достаточно. Еще отметим, что величины xi считаются неслучайными – если в каждой i ‑й точке проводится несколько измерений, то надо брать среднее. Случайными считаются только величины y .
Итак, в качестве исходных данных у нас имеется некий набор значений xi в количестве n штук. Надо провести кривую, соответствующую уравнению (5), так, чтобы сумма квадратов отклонений была минимальна:
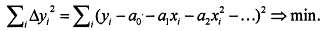
(6)
Какой степени полином должен быть? Из элементарной геометрии известно, что через две точки можно провести прямую (полином первой степени), через три – параболу (второй степени) и т. д., т. е. максимально возможная степень полинома на единицу меньше, чем число экспериментальных данных. Однако через две точки можно провести только одну прямую, и мы никогда не сможем оценить погрешностей – т. е. узнать, насколько наша прямая отличается от того, что имеет место в действительности. Поэтому чем избыток точек больше, тем лучше (в идеале необходимы те же 15–20 точек, но на практике для линейной зависимости можно обойтись и тремя‑пятью точками). Оптимальную же степень определяют так: строят несколько полиномов разной степени и смотрят на среднеквадратическое отклонение. Когда оно с увеличением степени полинома перестанет уменьшаться (или это уменьшение незначительно), то нужная степень достигнута.
|
|
|
Я не буду здесь вдаваться в подробности реализации метода наименьших квадратов – это бессмысленно, т. к. его обычно реализуют в виде готовой программы. Такую программу под названием RegrStat вы можете скачать с моей домашней странички по адресу http://revich.lib.ru из раздела Программы. Умеет строить простейшие регрессионные зависимости и Microsoft Excel, причем в том числе и как функцию от многих переменных, но только первого порядка (линейные полиномы). Ну, и конечно, существует множество специальных программных пакетов для этой цели.
Разновидности погрешностей
Мы в предыдущем изложении часто упоминали понятие погрешности, приводя его то в процентах, то в абсолютных величинах. Систематизируем эти представления и определим следующие три вида погрешностей:
□ абсолютная погрешность – в единицах измеряемой величины;
|
|
|
□ относительная погрешность – абсолютная, но выраженная в процентах от значения измеряемой величины;
□ относительная приведенная погрешность – абсолютная, но выраженная в процентах либо долях от всего диапазона измерений.
Последняя величина, если она соответствует стандартному ряду (например, 1,0; 0,75; 0,5; 0,25; 0,1 и т. п.), еще называется классом точности и обычно указывается в технических описаниях приборов.
При определении относительной приведенной погрешности учитывают все ошибки (их абсолютные значения): и случайную, и аддитивную, и мультипликативную погрешности. Причем в последнем случае за величину погрешности принимают значение мультипликативной погрешности в конце шкалы – ведь она зависит от измеряемой величины. Отсюда видно, что если мультипликативная погрешность доминирует, то выгоднее как можно больше «ужимать» диапазон измеряемых значений. С другой стороны, аддитивная и случайная погрешности от диапазона не зависят, и уменьшение его приведет к тому, что их вклад увеличится, – в частности, именно поэтому мы старались в схеме на рис. 13.4 «раздуть» выходное напряжение ОУ до максимума, ограничивая максимальный ток значением резистора R7, а не величиной напряжения.
Теперь мы можем грамотно ответить на вопрос, поставленный в начале раздела: если погрешность мультиметра на пределе 2 В составляет 0,5 %, то любое показываемое им значение на этом пределе (в том числе указанное нами ранее значение 1,000 В) отклонится от истинного значения не более, чем на ±10 мВ в 95 случаях из ста. А теперь оставим эти скучные материи и перейдем к куда более интересным вещам – к логическим микросхемам и цифровой электронике.
Часть III. ЦИФРОВОЙ ВЕК
ГЛАВА 14
На пороге цифрового века
Математическая логика и ее представление в технических устройствах
– Теперь давайте сочтем, сколько у нас всего. Портос?
– Тридцать экю.
– Арамис?
– Десять пистолей.
– У вас, Д'Артаньян?
– Двадцать пять.
– Сколько это всего? – спросил Атос.
– Четыреста семьдесят пять ливров! – сказал д'Артаньян, считавший, как Архимед.
А. Дюма . Три мушкетера
Все началось, конечно, с Аристотеля, который жил в IV веке до нашей эры. Когда читаешь вступление к любой популярной книге, посвященной чему угодно: от изящных искусств до биологии, химии, физики и математики, – возникает впечатление, что Аристотель был каким‑то сверхчеловеком. В самом деле, гении встречаются, но нельзя же быть гением настолько, чтобы разработать основы вообще всего, на чем зиждется современная цивилизация! Тем не менее, и авторы не врут, и Аристотель сверхчеловеком не был. Во‑первых, знаний было тогда накоплено еще не очень много, и обозреть их все – задача вполне посильная для человека острого ума и выдающихся способностей. Во‑вторых, Аристотель работал не один, его метод – коллективный мозговой штурм, это просто история донесла до нас фактически одно только его имя.
Но главное, пожалуй, в другом – древние рассматривали упомянутые нами дисциплины во взаимосвязи. Аристотель четко разделил только науку и ремесла («техно», по‑гречески), наука же делились на практические (этику и политику) и теоретические (физику и логику) дисциплины, но и они рассматривались как составные части единой науки. В чем древние, конечно, были более правы, чем мы, вынужденно поделившие области человеческой деятельности на множество автономных разделов.
Для нас важно, что главной составной частью науки считалась именно логика – искусство рассуждения. Вот она‑то и послужила той основой, из которой выросла цифровая техника и все многообразие информационных технологий, которые окружают нас теперь на каждом шагу.
Выдвинутые Аристотелем законы логики, которые с его же подачи стали идентифицироваться с законами мышления вообще, неоднократно пытались привести в математическую форму. Некто Луллий в XIII веке попытался даже механизировать процесс логических рассуждений, построив «Всеобщий решатель задач» (несомненно, это была первая попытка построения «думающей машины»). Формализацией логики занимался Лейбниц, искавший универсальный язык науки, и в конце концов все сошлось в двух работах английского математика Джорджа Буля, который жил и работал уже в середине XIX века. Любопытно название второй из этих работ – «Исследование законов мышления», первая же работа называлась поскромнее, но без «мышления» и тут не обошлось, – в названии фигурировало слово «рассуждения». То есть и сам Буль, и еще сто лет после него, до середины XX века, и все его предшественники в течение двух с большим лишком тысяч лет, прошедших со времен Аристотеля, – никто так и не усомнился, что в основе мышления лежит именно та логика, которая называется «аристотелевой». И лишь в XX веке, после работ Геделя и Тьюринга, и особенно в связи с благополучно провалившимися (как и у Луллия за 700 лет до того) попытками создания «искусственного интеллекта», до ученых, наконец, начало доходить, что мышление вовсе не имеет логической природы, а логика есть лишь удобный способ сделать свои рассуждения доступными окружающим.
Главное же следствие возникновения математической логики выявилось совсем не в исследованиях мышления, где оно виделось Лейбницу и Булю. Его обозначил в своей магистерской диссертации от 1940 года великий Клод Шеннон (рис. 14.1) – оказалось, что булевы законы в точности совпадают с принципами функционирования релейных электрических схем. Что самое поразительное – все компоненты, необходимые для моделирования законов логики с помощью электрических устройств (реле, выключатели), были известны еще до публикации Булем своих работ, но в течение еще почти ста лет никто не обращал на это внимания (Шеннон скромно утверждал, что случилось так, что до него просто никто не владел математикой и электротехникой одновременно). Не обратил на это внимание даже Чарльз Бэббидж, сконструировавший еще задолго до работ Буля механическую вычислительную («аналитическую») машину, – а ведь был знаком и с самим Булем, и с его работами!

Рис. 14.1. Клод Элвуд Шеннон (Claude Elwood Shannon), 1916–2001
Фото Lucent Technologies Inc /Bell Labs
Основные операции алгебры Буля
Булева алгебра имеет дело с абстрактными логическими переменными. Эти переменные можно интерпретировать по‑разному, но интерпретацию мы пока отложим.
Вне зависимости от интерпретации, для логических переменных определены некоторые операции, подчиняющиеся определенным правилам. Базовые операции такие:
□ операция логического сложения двух операндов – операция объединения, операция «ИЛИ» («OR»), обозначается обычным знаком сложения;
□ операция логического умножения двух операндов – операция пересечения, операция «И» («AND»), мы будем обозначать ее крестиком, чтобы отличить от обычного умножения;
□ операция отрицания для одного операнда – операция «НЕ» («NOT»), обозначается черточкой над символом операнда.
В математике операция логического сложения (дизъюнкция) обозначается еще знаком v , а умножения (конъюнкция) – ^ . Кроме того, операция умножения часто обозначается знаком & , и это обозначение нам встретится, когда мы перейдем к микросхемам. Остальные операции могут быть записаны как сочетания этих трех основных.
Любая конкретная интерпретация булевых операндов – математическая или техническая – должна отвечать правилам булевой алгебры. Например, оказалось, что этим правилам отвечают множества (отсюда другие названия тех же операций: «пересечение» и «объединение»). Программисты имеют дело с логическими переменными 0 и 1, которые также есть одно из представлений булевых операндов.
Следует отчетливо понимать, что вне зависимости от интерпретации (включая и напряжения в релейных цепях по Шеннону), любые булевы объекты ведут себя одинаково: так, операция пересечения множеств совершенно адекватна операции «И» с логическими переменными или соответствующей манипуляции с выключателями в электрической сети.
В булевой алгебре многое совпадает с обычной – например, справедливы правила типа А + В = В + А или А + (В + С) = (А + В) + С), но для нас важны как раз отличия.
Вот они: А + А = А (а не 2А, как было бы в обычной алгебре), а также А х А = А (а не А2). Последнее уравнение в обычной алгебре, впрочем, имело бы решение, причем сразу два: 0 и 1. Таким путем обычно и переходят к интерпретации булевых операндов, как логических переменных, которые могут иметь только два состояния: 1 и 0 или «правда» (true ) и «ложь» (false ). В этом представлении мы действительно можем попробовать с помощью определенных ранее операций записывать некоторые высказывания в виде уравнений и вычислять их значения, что дает иллюзию формального воспроизведения процесса мышления. Но сначала надо определить, как и в обычной алгебре, правила, которым подчиняются операции, – т. е. таблицу логического сложения и таблицу логического умножения. Они таковы:

Операция отрицания «НЕ» меняет 1 на 0 и наоборот.
Примеры записи логических выражений обычно приводят для каких‑нибудь бытовых высказываний, но мы поступим нетрадиционно: приведем пример из области математики. Пусть высказывание состоит в следующем:«x меньше нуля или х больше 1 и у меньше 2». Как записать это высказывание? Введем следующие логические переменные: А = (х < 0); В = (х > 1); С = (у < 2). Как мы видим, все они могут принимать только два значения: «правда» (если условие выполняется) и «ложь» (если не выполняется). Обозначим значение всего выражения через D . Тогда высказывание записывается так:
D = (A + B ) x C (1)
Можно записать и так:
D = (A ИЛИ B ) И C
Или так:
D = (A OR B ) AND C
Или, наконец, так:
D = ((х < 0) OR (х > 1)) AND (у < 2)
Последняя запись хорошо знакома всем, кто изучал язык программирования Pascal . На языке С та же запись выглядит непонятнее:
D =((x < 0)||(x > 1))&&(y < 2)
* * *
Подробности
О великий и могучий язык С ! В нем самую простую вещь можно запутать до полной потери смысла. В нашем случае то же самое выражение можно было бы записать, как ((х < 0) | (х > 1)) & (у < 2), и ничего бы не изменилось. В этом языке (в отличие от Pascal ) есть две разновидности логических операций: обычные («логическое И» &&, «логическое ИЛИ» ||) и поразрядные («поразрядное И» &, «поразрядное ИЛИ» |). Есть и, соответственно, «логическое НЕ» (!) и «поразрядное НЕ» (~). Термин «поразрядные» означает, что они применимы к многоразрядным двоичным числам. В результате их применения тоже получается многоразрядное двоичное число, необязательно ноль или единица, как в случае логических. Поскольку наши результаты операций сравнения содержат только один двоичный разряд (либо соблюдается, либо не соблюдается), то в данном случае логические и поразрядные операции оказываются идентичны, и можно писать и так, и так. А вот если в операциях участвуют обычные числа, то результат будет разный: «10&&7» равно «логической 1» (отличное от нуля значение всегда интерпретируется, как «правда»), тогда как «10&7» равно 2 (почему, будет рассказано далее). Как мы узнаем в главе 21 , эти особенности играют большую роль в программировании микроконтроллеров на языке С .
* * *
Пусть х = 0,5, у = 1. Чему будет равно D в этом случае? Очевидно, что выражение (А + В) примет значение «ложь» (0), поскольку х не удовлетворяет ни одному из условий А и В. Переменная С примет значение «правда» (1), но на результат это уже не повлияет, т. к. произведение 0 на 1, согласно таблице логического умножения, равно 0. То есть D в данном случае есть «ложь». Если же принять значение х = ‑0,5, оставив у равным 1, то D примет значение «правда».
Интересный оборот примут события, если вместо «OR» между А и В поставить «AND», – легко догадаться, что выражение в скобках тогда не будет «правдой» ни при каком значении х , поскольку условия «х меньше 0» и «х больше 1» взаимоисключающие. Потому результирующее условие D всегда будет принимать значение 0, т. е. «ложь». Но вот если мы изменим выражение следующим образом:
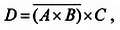
(2)
то есть инвертируем выражение в скобках с помощью операции «НЕ», то получим обратный результат: D всегда будет «правдой» (черточкой над символом или выражением как раз и изображается инверсия). Интересно, что тот же самый результат мы получим, если запишем выражение следующим образом:
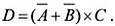
(3)
Это свойство выражается в так называемых правилах де Моргана (учителя Буля ):
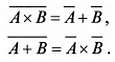
Отметим, что из таблиц логического умножения и сложения вытекает еще одно любопытное следствие. Дело в том, что ассоциация значения «ложь» с нулем, а «правды» с единицей (положительная логика), есть действие вполне произвольное – ничто не мешает нам поступить наоборот (отрицательная логика). Такая замена приводит к тому, что все операции «ИЛИ» меняются на «И» и наоборот (рассмотрите таблицы внимательно). А вот операция «НЕ» к такой замене индифферентна – 0 меняется на 1 в любой логике.
Далее приведены несколько соотношений, которые вместе с правилами де Моргана помогают создавать и оптимизировать логические схемы. Некоторые из них очевидны, иные же – совсем нет.
Ассоциативный закон умножения:
A x B x C = (A x B ) x C = A x (B x C )
Ассоциативный закон сложения:
A + B + C = (A + B ) + C = A + (B + C )
Другие формулы:
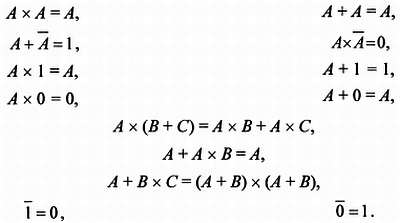
Дата добавления: 2019-02-12; просмотров: 222; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
