Задание ФАЛ при помощи диаграмм Венна
Диаграммы Венна, названные по имени священника Джона Венна [3], применявшего их в исследованиях по логике, являются графическим представлением, демонстрирующим соотношения между множествами. На основе соответствия между теорией булевой алгебры и теорией множеств диаграммы Венна очень полезны для визуального представления аксиом и законов булевой алгебры, однако их не следует использовать для построения доказательств тождеств, поскольку большинство общих положений эти диаграммы показать не могут. На рисунке 2.8 приведены диаграммы Венна для констант «0», «1» и элементарных функций логического умножения, сложения и инверсии. Область, ограниченная кружком на рисунке, соответствует одной переменной. На рисунке 2.9 представлена диаграмма Венна для функции 
.
 |
Задание ФАЛ с использованием контактных схем
Контактная схема может рассматриваться как техническая модель логических выражений. Одну из первых моделей предложил в 1910 году физик П.С. Эренфест [3], в которой использована аналогия между высказываниями и электрическими контактами, поскольку и те и другие имеют двоичную природу. На рисунке 2.10 приведены контактные модели для констант 0, 1 и элементарных функций логического умножения, сложения и инверсии. Обозначение Uип на рисунках указывает на положительный полюс источника питания.
На рисунке 2.11 представлена реализация на контактах функции .
|
|
|
КАНОНИЧЕСКИЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ ФАЛ
При минимизации ФАЛ часто приходится представлять исходные выражения в нормальном (каноническом) виде, т.е. пользоваться так называемыми каноническими формами ФАЛ [1]. Рассмотрим их подробнее.
К каноническим (общепринятым) формам представления ФАЛ относятся:
1) ДНФ (дизъюнктивная нормальная форма);
2) СДНФ (совершенная дизъюнктивная нормальная форма);
3) КНФ (конъюнктивная нормальная форма);
4) СКНФ (совершенная конъюнктивная нормальная форма).
Определение. Элементарной конъюнкцией называется конъюнкция (логическое умножение) любого числа различных независимых переменных, входящих в данную конъюнкцию с инверсией или без нее не более одного раза. Например, 
Определение. Элементарной дизъюнкцией называется дизъюнкция (логическое сложение) любого числа различных независимых переменных, входящих в данную дизъюнкцию с инверсией или без нее не более одного раза. Например, 
Определение. Дизъюнктивной нормальной формой называется дизъюнкция любого числа элементарных конъюнкций. Например, 
Совершенная ДНФ содержит в каждом члене все аргументы или инверсии заданной функции.
|
|
|
Например, 
Определение. Конъюнктивной нормальной формой называется конъюнкция любого числа элементарных дизъюнкций. Например, 
Совершенная КНФ содержит в каждой скобке все аргументы или их инверсии.
Например 
.
Формы СДНФ и СКНФ используются в процессе синтеза ДУ для перехода от табличной формы представления функций алгебры логики к аналитической, а также являются базовыми для различных методов минимизации, особенно связанных с применением персональных компьютеров.
Для получения СДНФ по ТИ необходимо проанализировать значение функции на всех наборах аргументов. Каждое единичное значение функции дает один член (одну конъюнкцию) в формуле СДНФ. Все члены (все конъюнкции) соединяются между собой знаками дизъюнкции. Таким образом, число конъюнкций равно числу единиц в значении функции в ТИ.
Каждая конъюнкция состоит из произведения аргументов функции, а каждый аргумент в формуле записывается без инверсии, если в ТИ он равен единице, или с инверсией, если в ТИ он равен нулю.
Например для таблицы 3.1, СДНФ будет иметь следующий вид: 
Для перехода от ДНФ к СДНФ необходимо добавить к каждому члену (конъюнкции) недостающие аргументы, используя закон дополнительности до единицы. Например,
|
|
|
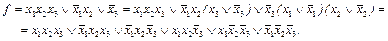
Форма ДНФ является упрощенной, т.е. позволяет построить схему с меньшим числом элементов, чем при форме СДНФ.
При переходе от СДНФ к ДНФ можно использовать для упрощения формулы законы АЛ или любые другие способы минимизации функций.
Форма СКНФ также получается по ТИ. В СКНФ присутствует столько скобок, сколько нулей имеет функция в ТИ. Каждая скобка соединяется знаком конъюнкции.
Для получения аргументов в скобках используются следующие правила.
1) Если значение аргументов в ТИ равно нулю, то в формуле этот аргумент записывается без инверсии.
2) Если же в ТИ значение аргумента равно единице, то он записывается в формулу с инверсией.
Все аргументы в скобке соединяются между собой знаками дизъюнкции. Для таблицы 3.1 СКНФ будет иметь следующий вид:
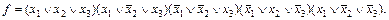
Для перехода от КНФ к СКНФ необходимо, используя законы и правила АЛ (в основном закон дополнительности до нуля), добавить к каждому члену (в каждой скобке) недостающий аргумент.
Например, 
Большая часть методов минимизации ориентирована на получение минимальной дизъюнктивной нормальной формы (МДНФ).
Определение. Число переменных, входящих в конъюнкцию дизъюнктивной нормальной формы, называется рангом конъюнкции. Для СДНФ ранг конъюнкции равен числу аргументов функции.
|
|
|
Определение. Две конъюнкции называются соседними, если они различаются значением только одной переменной. Например, 
Определение Конъюнкция (n – 1) переменной, полученная в результате склеивания соседних конъюнкций (конституентов) по закону склеивания 
называется минтермом (n – 1) ранга; конъюнкция (n – i) переменных, полученная склеиванием соседних минтермов [n – (i –1)]-го ранга, называется минтермом (n – i)-го ранга.
Например, в выражении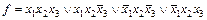 
после применения закона склеивания получатся следующие минтермы 2-го ранга: 
и функция после первой итерации применения закона склеивания будет состоять из дизъюнкции минтермов 2-го ранга 
Применив закон склеивания к полученной функции второй раз, получим минтерм 1-го ранга x2. Причем, этот минтерм будет реализовывать ту же ТИ, что и исходная функция, т.е. 
Определение. Конституенты (минтермы) функции, к которым не применима операция склеивания, называются простыми или первичными импликантами.
Определение. Простой импликант называется существенным, если он образован склеиванием таких конституентов, что по крайней мере для одного из них эта операция была единственной.
Определение. ДНФ ФАЛ, составленная из простых импликантов, некоторые члены которой могут быть избыточными и удалены без нарушения эквивалентности исходной функции, называется сокращенной.
Определение. ДНФ ФАЛ называется тупиковой, если ни один ее член не может быть удален без нарушения эквивалентности исходной функции. К минтермам тупиковой ДНФ (ТДНФ) операция склеивания неприменима.
Определение. ТДНФ называется минимальной, если она содержит наименьшее число вхождений переменных по сравнению с другими ТДНФ. Минимальная форма функции обязательно содержит существенные импликанты.
Можно выделить два направления в решении задачи минимизации.
Первое состоит в отыскании простых импликантов, построении из них тупиковых форм и определении путем перебора минимальной ДНФ.
Второе направление заключается в нахождении всех существенных импликантов, отыскании недостающих для реализации заданной функции простых импликантов и построении ТДНФ.
Каждое из обоих направлений включает целый ряд методов. Рассмотрим некоторые из них.
МИНИМИЗАЦИЯ ФАЛ
Общие положения
При разработке ДУ обычно возникает задача оптимизации их структуры, т.е. получения экономичной и надежной технической реализации [2, 3]. Это означает, что из двух схем ДУ, выполняющих одинаковые функции, следует выбирать ту, которая содержит меньшее число элементов, а при одинаковом числе элементов – ту, суммарное число входов используемых элементов которой будет наименьшим.
Решение этой задачи связано с проблемой минимизации (упрощения, сокращения) ФАЛ, реализующих данное ДУ.
Минимизация – это процесс нахождения такого эквивалентного выражения ФАЛ, которое содержит минимальное число вхождений переменных. При минимизации могут быть различные варианты: получение выражений с минимальным числом инверсных переменных либо с минимальным числом вхождений какой-либо одной переменной и т.д.
Для минимизации функций и поиска наиболее экономичной схемы, реализующей заданное выражение, до сих пор не найдено эффективных алгоритмов, позволяющих решать эти задачи целенаправленно и быстро. Гарантированно найти минимальное выражение для произвольной функции можно лишь методом полного перебора вариантов различных способов группировки в процессе минимизации, а это реально осуществимо лишь при небольшом числе аргументов. С ростом их числа сложность минимизации и поиска экономичной схемы растет экспоненциально и очень скоро становится не под силу ни человеку, ни ЭВМ.
С точки зрения подходов к упрощению логических выражений функции, с которыми имеет дело схемотехник, удобно разделить на три группы: функции малого числа аргументов; «объективные» функции многих аргументов и «субъективные» функции многих аргументов.
К первой группе можно отнести функции двух–пяти аргументов. Статистический анализ реальных схем цифровой аппаратуры показывает, что разработчики в подавляющем большинстве случаев сталкиваются именно с необходимостью реализовывать именно такие функции. Благодаря малому числу переменных таблицы таких функций короткие, вариантов группировки при минимизации не слишком много, хорошо работает наиболее наглядное геометрическое представление, и в общем, минимизация таких функций любым способом серьезных проблем не вызывает.
Ко второй группе – громоздких «объективных» функций – относятся функции более пяти переменных, которые были получены не человеком, а отражают некую объективную природную зависимость. Для этих функций характерно следующее. Во-первых, в них не заложено какой-либо простой логической закономерности, которую можно угадать и использовать для минимизации, т.е. таблица такой функции это просто некая случайная последовательность единиц и нулей. Во-вторых, в силу значительного числа переменных полный перебор вариантов при любом способе поиска минимальной или любой другой экономичной формы практически неосуществим. И, в-третьих, что самое важное, из теоремы О.Б. Лупанова об оценке сложности функций следует, что с ростом числа аргументов доля экономичных по оборудованию функций стремится к нулю, т.е. почти все функции оказываются неупрощаемыми. Следовательно, задача поиска минимальных форм «объективных» функций многих аргументов не только сложна и громоздка, но и с большой вероятностью безнадежна. Это учитывают изготовители элементов, выпуская для реализации функций многих переменных специальные микросхемы – программируемые логические матрицы (ПЛМ) и постоянные запоминающие устройства (ПЗУ). При использовании наиболее распространенных простых вариантов ПЛМ реализация функций будет самой экономичной по затратам аппаратуры, если функция приведена не к минимальной, а к кратчайшей форме. Если же при минимизации ДНФ самую короткую форму получить не удалось, то проигрыш оказывается небольшим, поскольку стоимость реализации на ПЛМ каждой элементарной конъюнкции ДНФ невелика – 1/50 стоимости корпуса. Одной из целей освоения промышленностью ПЛМ как раз и была экономия труда разработчиков схем.
При использовании ПЗУ на них реализуется непосредственно ТИ функции, т.е. ни записи ФАЛ, ни тем более ее минимизации не требуется вообще.
К третьей группе – «субъективных» функций многих аргументов ‑ относятся функции, составленные человеком. Особенность их связана с понятием декомпозиции. Это значит, что сложная ФАЛ разбивается на более простые составляющие, из минимальных форм которых в конечном итоге строится аппаратная реализация ДУ. Однако декомпозиция может быть выполнена неудачно, и устройство в результате будет неэффективным. Для того чтобы избежать этого существуют специальные методы декомпозиции, которые позволяют получать приемлемый результат.
Рассмотрим методы минимизации в применении к первой группе функций как наиболее часто и повсеместно встречающихся.
Если значение ФАЛ однозначно определено на всех возможных наборах значений ее аргументов, то она называется полностью определенной (заданной). Если же на некоторых наборах значение функции является безразличным и однозначно не определено, то такая функция называется неполностью или частично заданной.
В соответствии с этим разделим и методы минимизации (упрощения) ФАЛ на две группы: методы минимизации полностью заданных ФАЛ и методы минимизации неполностью заданных ФАЛ.
Дата добавления: 2019-02-12; просмотров: 517; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!