Задание ФАЛ с использованием диаграмм двоичного решения

Стр 1 из 7Следующая ⇒

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра автоматики и телемеханики

Ю. Ф. БЕРЕЗНЯЦКИЙ

ЗАДАНИЕ И МИНИМИЗАЦИЯ

ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ

Пособие для практических занятий
по дисциплине «Теория дискретных устройств»

Гомель 2004
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра автоматики и телемеханики

Ю. Ф. БЕРЕЗНЯЦКИЙ

ЗАДАНИЕ И МИНИМИЗАЦИЯ

ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ

Пособие для практических занятий

по дисциплине «Теория дискретных устройств»

Одобрено методической комиссией

электротехнического факультета

Гомель 2004

УДК 656.25-192

Б866

Р е ц е н з е н т – канд. физ.-мат. наук, зав. кафедрой «Микропроцессорная техника и информационно-управляющие системы» Н.В. Рязанцева

Березняцкий Ю.Ф.

Б866 Задание и минимизация функций алгебры логики: Пособие для практических занятий по дисциплине «Теория дискретных устройств». – Гомель: БелГУТ, 2004. – 44 с.

Рассматриваются вопросы задания и минимизации полностью и неполностью заданных функций алгебры логики при помощи законов алгебры логики, карт Карно, методами Квайна, Квайна–Мак-Класки и существенных переменных.

Предназначено для студентов электротехнического факультета и ФБО в качестве руководства по минимизации функций алгебры логики при выполнении практических занятий. Пособие также может использоваться студентами при выполнении курсового проекта по дисциплине «Теория дискретных устройств».

УДК 656.25-192

ВВЕДЕНИЕ

Современные системы автоматики, телемеханики и связи (АТ и С) имеют преимущественно электронное, микроэлектронное и микропроцессорное исполнение. Подавляющее большинство выпускаемых промышленностью и разрабатываемых систем АТ и С являются дискретными.

Поэтому для успешного усвоения принципов их функционирования и анализа работы необходимы знания в области теории дискретных устройств (ТДУ). ТДУ – это дисциплина, изучающая принципы анализа и синтеза устройств, построенных на базе дискретных элементов (ДЭ). Под дискретным элементом понимается минимальная совокупность деталей, объединенных в общую схему для выполнения заданной функции и меняющих свое выходное значение скачкообразно при определенном изменении входной величины. К простейшим ДЭ относятся реле, диоды, транзисторы, тиристоры и т.д.

Данное пособие дает основные навыки по применению основных аксиом и законов алгебры логики в ТДУ, что позволяет в конечном итоге реализовывать схемы дискретных устройств наиболее оптимальным образом.

ПОНЯТИЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ

Большая часть методов анализа и синтеза всех классов дискретных устройств основана на применении положений алгебры логики (АЛ) [1–4]. АЛ является разделом математической логики. В АЛ все операции проводятся с переменными, принимающими лишь два значения – «истина» и «ложь». Для теории дискретных устройств значение «истина» соответствует логической единице «1», а значение «ложь» – логическому нулю «0». Поэтому АЛ называют еще двухзначной или булевой, по фамилии ее основоположника ирландского математика Дж. Буля (1815–1864) [3].

Возможность применения АЛ для синтеза и анализа реальных дискретных устройств (ДУ) обусловлена использованием в них двоичных сигналов и двустабильных элементов, имеющих два четко выраженных состояния. Например, состояние реле соответствует «1», если оно находится под током, а если реле обесточено – его состояние соответствует «0».

В теории дискретных устройств (ТДУ) часто оперируют таким понятием, как функция алгебры логики (ФАЛ) [1, 3, 4].

Функция 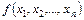называется ФАЛ в том случае, если она и ее переменные могут принимать лишь два взаимоисключающих значения «0» и «1».

Переменные ФАЛ (ее аргументы) сопоставляют со значениями сигналов на входах ДУ, а значения ФАЛ (ее результат) – со значениями сигналов на выходах ДУ.

Поскольку реальные ДУ имеют конечное число входов, то мы будем рассматривать функции конечного числа аргументов. Для n двоичных переменных x₁, x₂, …, x_n существует k = 2ⁿ наборов значений переменных и R = 2^k различных ФАЛ. Например, для одного аргумента x₁ существует k = 2¹ = 2 набора переменных {x₁= 0, x₁ = 1} и R = 2² = 4 функции алгебры логики f₀ = 0 (константа нуль), f₁ = 1 (константа единица), f₂ = x₁ (повторение x₁) и 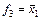(инверсия x₁, т.е. замена всех его значений на обратные).

Так как число аргументов и число значений каждого аргумента конечны, конечна и область определения любой ФАЛ.

СПОСОБЫ ЗАДАНИЯ ФАЛ

Существует множество способов задания ФАЛ. Среди них наиболее известны такие способы, как [1]:

1) табличный;

2) графический;

3) координатный (при помощи карт Карно);

4) числовой;

5) аналитический;

6) на основе диаграмм двоичного решения;

7) при помощи диаграмм Венна;

8) с использованием контактных схем.

Рассмотрим указанные способы задания подробнее.

Табличный способ

При этом способе ФАЛ задается таблицей зависимости выходных значений от входных наборов. Такая таблица называется таблицей истинности (ТИ). Для n аргументов ТИ содержится k = 2ⁿ строк (по числу наборов значений аргументов) и (n + 1) столбцов – по числу аргументов плюс один столбец значений функции. В ТИ каждому набору аргументов соответствует свое значение функции. Таблицы 2.1, 2.2 и 2.3 представляют собой ТИ от 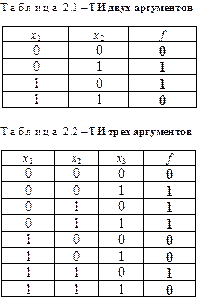двух, трех и четырех аргументов соответственно.

При этом таблица 2.1 содержит k = 2² = 4 строки, таблица 2.2 содержит k = 2³ = 8 строк, а таблица 2.3 – k = 2⁴ = 16 строк.

Для того чтобы задать все ФАЛ от n аргументов, необходимо построить 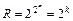таблиц истинности или объединить их в одну совокупную ТИ. Так, если число аргументов n = 2, то число наборов (количество строк в ТИ) будет k = 2² = 4, а количество ТИ для задания всех ФАЛ от двух переменных R = 2^k = 2⁴ = 16. После объединения всех ФАЛ в одной совокупной ТИ, можно проследить основные характеристики взаимосвязи ФАЛ от двух переменных (таблица 2.4).

Одна половина функций в таблице 2.4 инверсна (обратна по значению) другой ( 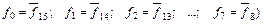, остальные являются константами (f₀; f₁₅). Кроме того ряд функций аналогичен функциям от одной переменной (f₃ = x₁; f₅ = x₂; 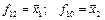), т.е. эти функции существенно не зависят от одного из аргументов. Если функция существенно не зависит от аргумента x_m, то выполняется условие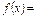 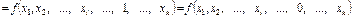, а аргумент x_m называют фиктивным.

Т а б л и ц а 2.4 – ФАЛ двух аргументов

x₁	x₂	f₀	f₁	f₂	f₃	f₄	f₅	f₆	f₇	f₈	f₉	f₁₀	f₁₁	f₁₂	f₁₃	f₁₄	f₁₅
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Обозначение		Х	·	D	Х	D	Х	Å	Ú	¯	µ	¯	®	¯	®	\|	Х

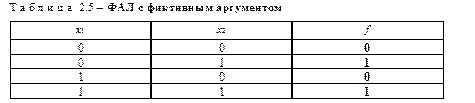
В противном случае функция является существенно зависящей от аргумента x_m. Например, в таблице 2.5 аргумент x₁ является фиктивным, и функция существенно зависит от аргумента x₂.

Рассмотрим остальные ФАЛ в таблице 2.4:

f₁ – функция «И» (логическое умножение, конъюнкция). Обозначается f₁ = x₁×x₂, или f₁ = x₁& x₂, или f₁ = x₁ Ù x₂. Данная функция будет равна нулю, если хотя бы один из ее аргументов равен нулю, и, равна единице только тогда, когда оба ее аргумента равны единице;

f₂ – запрет второго аргумента. Обозначается 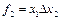, или , или ;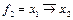

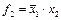f₄ – запрет первого аргумента. Обозначается , или , или ;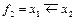

f₆ – сумма по модулю два (функция неравнозначности). Обозначается ;

f₇ – функция «ИЛИ» (логическое сложение, дизъюнкция). Обозначается f₇ = x₁ Ú x₂ либо f₇ = x₁ + x₂. Данная функция будет равна нулю только в том случае, если оба ее аргумента равны нулю. Во всех остальных случаях она равна единице;

f₈ – функция «ИЛИ-НЕ» (функция Вебба). Она реализует операцию «стрелка Пирса». Обозначается ;

f₉ – эквивалентность (функция равнозначности). Обозначается ;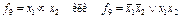

f₁₁ – импликация второго аргумента. Обозначается 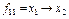или ;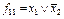

f₁₃ – импликация первого аргумента. Обозначается 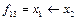или ;

f₁₄ – функция «И-НЕ» (функция Шеффера). Она реализует операцию «штрих Шеффера». Обозначается

Все приведенные в таблице 2.4 функции называются элементарными. Элементарные функции позволяют реализовать на их основе сколь угодно сложное логическое (дискретное) устройство.

Табличный способ задания ФАЛ является достаточно универсальным, однако он обладает тем недостатком, что при большом числе аргументов ТИ становится излишне громоздкой.

Графический способ

Данный способ задания ФАЛ основан на сопоставлении наборам значений переменных ФАЛ точек n-мерного пространства. При этом множество наборов 2ⁿ определяет число вершин n-мерного единичного квадрата или куба, которым приписаны значения функции на этих наборах. Куб или квадрат называют единичным, так как каждое их ребро соединяет вершины, наборы которых различаются только одной переменной.

ФАЛ задается единичным квадратом, если она зависит от двух переменных. Так, например, для таблицы 2.1 ФАЛ можно задать в виде квадрата, показанного на рисунке 2.1.

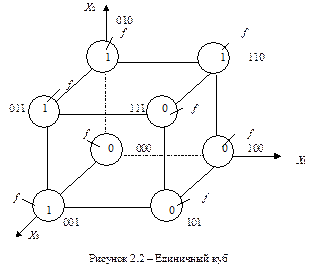
ФАЛ задается единичным кубом, если она зависит от трех аргументов. Так для таблицы 2.2 ФАЛ будет задана кубом, показанным на рисунке 2.2.

Графический способ задания ФАЛ является достаточно наглядным, однако он может быть использован при двух и трех аргументах, реже четырех или пяти. Как правило, если число аргументов функции более трех, то используют другие способы задания ФАЛ.

Координатный способ

При координатном способе ФАЛ задается в виде координатной карты состояний (карты Карно). Карта состояний представляет собой прямоугольную таблицу, разделенную на клетки. Общее число клеток карты равно числу наборов функции k = 2ⁿ, а все переменные ФАЛ разделяются на определяющие строки и определяющие столбцы карты.

На пересечении строки и столбца расположена клетка, в которую записываются значения ФАЛ на выбранном наборе переменных. Разделение переменных на группы выполняется таким образом, чтобы в соседних клетках наборы различались значением лишь одной переменной.

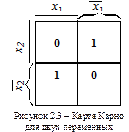Приведем примеры карт Карно, соответствующих таблицам 2.1, 2.2 и 2.3. Для таблицы 2.1 карта Карно имеет k = 2² = 4 клетки. Она представлена на рисунке 2.3.

Как видно из рисунка 2.3 для каждого аргумента карта состояний разбивается на две части. Одна половина карты соответствует прямому значению аргумента (под прямой чертой), а другая – инверсному его значению (под фигурной скобкой).

Для таблицы 2.2 карта состояний должна иметь k = 2³ = 8 клеток. Она представлена на рисунке 2.4. Карта увеличивается в два раза при увеличении количества аргументов на единицу.

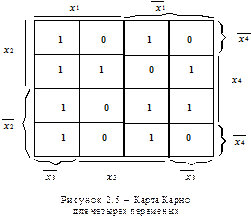
При четырех переменных карта Карно имеет k = 2⁴ = 16 клеток. Для таблицы 2.3 она имеет вид, показанный на рисунке 2.5.

Карта для пяти переменных содержит 2⁵ = 32 клетки.При этом общая карта состоит как бы из двух четырехмерных подкарт, расположенных одна над другой. Практически такой вариант неприемлем, поэтому подкарты располагают в одной плоскости (рисунок 2.6). Подкарта 1 располагается под прямым значением переменной х₅, а подкарта 2 – под инверсным значением этой переменной.

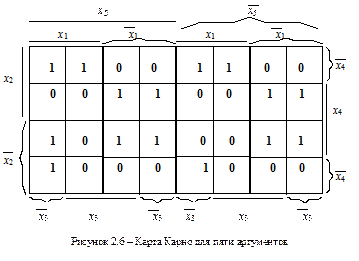
Координатный способ задания ФАЛ, наряду с табличным, находит очень широкое применение. Однако он имеет недостаток, связанный с ограничением числа переменных. Обычно координатный способ используется при числе переменных до четырех, реже – до пяти, шести.

Числовой способ

При числовом способе задания ФАЛ каждому набору переменных ставится в соответствие определенное число в двоичной системе исчисления и присваивается ему соответствующий десятичный номер. Функция задается в виде десятичных номеров, на которых она принимает единичные (первый вариант числового задания) или нулевые (второй вариант числового задания) значения.

Так, например, для таблицы 2.1 по первому варианту ФАЛ будет записана следующим образом: f = {1, 2}_x₁_x₂, а по второму варианту – f = Ù{0, 3}_x₁_x₂. Для таблицы 2.2 числовая запись ФАЛ по первому варианту имеет вид f = {1, 2, 3, 6}_x₁_x₂_x₃, по второму варианту – f = Ù{0, 4, 5, 7}_x₁_x₂_x₃, а для таблицы 2.3 (первый вариант) f = {1, 2, 3, 5, 6, 8, 9, 12, 13, 15}_x₁_x₂_x₃_x₄и f = Ù{0, 4, 7, 10, 11, 14}_x₁_x₂_x₃_x₄(второй вариант). Знак «Ù» во втором варианте записи указывает на то, что используются наборы нулевых значений функции.

В приведенных выражениях в фигурных скобках через запятую записаны в порядке возрастания номера наборов, на которых ФАЛ равна «1» (счет ведется с нуля). Сразу же за фигурными скобками проставляются в виде индексов аргументы ФАЛ, начиная со старшего разряда.

Данный способ задания ФАЛ является одним из наиболее простых, однако, его недостаток – слабая наглядность.

Аналитический способ

При данном способе ФАЛ задается в виде алгебраического выражения, получаемого при применении каких-либо логических операций к переменным.

Алгебраическое выражение показывает, какие логические операции должны выполняться над аргументами функции, и какова должна быть их последовательность.

Например, применяя операции инверсии, конъюнкции и дизъюнкции можно задать функцию 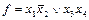или функцию .

Недостаток данного способа в отсутствии наглядности, а преимущество – в возможности применения математического аппарата для операций с переменными.

Задание ФАЛ с использованием диаграмм двоичного решения

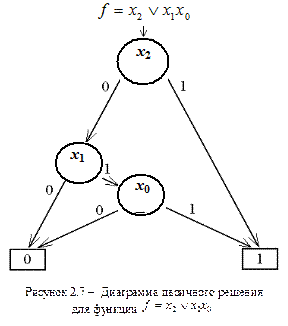
Диаграмма двоичного решенияявляется разновидностью корневого ориентированного графа. Она обеспечивает полное, краткое и простое описание сложных цифровых функций. На рисунке 2.7 приведена диаграмма двоичного решения для функции .

На рисунке 2.7 прямоугольники с цифрами 0 и 1 соответствуют окончательным значениям ФАЛ. Узлы, обозначенные кружками, соответствуют переменным, от которых зависит ФАЛ, а цифры у ветвей – значениям этих переменных. Диаграммы двоичного решения широко используются для анализа сложных функций, формирования тестов, задач верификации и т.д.

Дата добавления: 2019-02-12; просмотров: 436; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!