Целочисленное программирование

⇐ ПредыдущаяСтр 6 из 6

На практике часто встречаются задачи, совпадающие по постановке с задачами линейного программирования, но отличающиеся той особенностью, что искомые значения переменных должны быть целыми. Такие задачи называются задачами целочисленного программирования.

Отыскание решения таких задач сопряжено со значительными трудностями. В частности, невозможно применение стандартных приемов, состоящих в замене дискретной задачи ее непрерывным аналогом, и дальнейшем округлении найденного решения до ближайшего целочисленного.

Таким образом, для решения задач дискретного программирования необходимы специальные методы.

Методы решения задач дискретного программирования по принципу подхода к проблеме делят на группы:

1) методы отсечения или отсекающих плоскостей;

2) метод ветвей и границ;

3) методы случайного поиска и эвристические методы.

Рассмотрим метод ветвей и границ, так как он наиболее прост.

Этот метод относится к группе комбинаторных методов дискретного программирования и является одним из наиболее распространенных методов этой группы.

Пусть имеется задача дискретного программирования в общей форме: надо определить максимум целевой функции

F = c₁x₁ + c₂x₂ + ... + c_nx_n (2.48)

при наличии ограничений

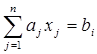, i = 1, …, m; (2.49)

x_j ³ 0, x_j – целое число.

В основу метода ветвей и границ положены следующие построения, позволяющие в ряде случаев существенно уменьшить объем перебора вариантов.

Первоначально находится оптимальный план задачи без учета целочисленности переменных, обозначим этот план через X_o.

Если среди X_o нет дробных чисел, то тем самым найдено исходное решение поставленной задачи и максимальное значение целевой функции F_max = F (X_o).

Если среди компонентов этого плана имеются дробные числа, то решение X_o не удовлетворяет условию целочисленности и необходимо осуществить упорядоченный переход к новым планам до тех пор, пока не будет найдено решение задачи.

Для всякого последующего плана X значение целевой функции на этом плане будет меньше оптимального

F(X_o) ³ F(X). (2.50)

Пусть среди компонентов плана есть дробные числа. Предположим, что x _io принимает дробное значение, тогда в оптимальном целочисленном решении значение этой переменной будет, по крайней мере, меньше или равно ближайшему меньшему целому числу K_io, либо больше или равно ближайшему большему целому числу K_io+ 1.

Далее, определив K_io, переходим к решению следующих двух задач.

I	II
F = c₁x₁ + ... + c_nx_n ® max	F = c₁x₁ + ... + c_nx_n ® max
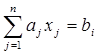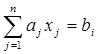, i = 1, …, m	, i = 1, …, m
x _j ³ 0, x _jo £ K_jo	x_j ³ 0, x_jo ³ K_{jo + 1}

Решаем обе задачи и найдем X _I и X _II. Далее возможен один из четырех вариантов:

1) одна из этих задач не имеет решения, а вторая имеет оптимальное целочисленное решение, оно и будет искомым;

2) одна из этих задач неразрешима, а вторая имеет оптимальное решение, среди компонентов которого есть дробные числа, тогда необходимо перейти к двум задачам вида I и II, но к имеющимся ограничениям добавляем ограничение на следующую дробную переменную;

3) обе задачи разрешимы. Одна имеет целочисленный оптимальный план, а другая имеет дробное решение. Тогда вычисляется F (X_I) и F (X_II), эти значения сравниваются. Если для целочисленного решения значение целевой функции не меньше значения функции на дробном решении, то данное целочисленное решение является оптимальным для исходной задачи. Если же значение целевой функции больше на дробном плане, то необходимо рассматривать задачу с дробным оптимальным решением и для нее составить пару задач аналогичных I и II;

4) обе задачи разрешимы, в оптимальном решении обеих задач имеются дробные числа, вычисляются значения F (X_I) и F (X_II), и выбирается то решение и та задача, для которой решение (значение) целевой функции максимально и для этой задачи составляются задачи, аналогичные I и II.

Эти операции осуществляются до тех пор, пока не дойдем до целочисленного решения.

Таким образом, описанный выше итерационный процесс может быть представлен в виде некоторого дерева (рис. 5), на котором исходная вершина отвечает оптимальному плану X ₀ задачи линейного целочисленного программирования, а каждая соединенная с ней ветвью вершина отвечает оптимальным планам задач I и II. Каждая из этих вершин имеет свои ветвления. При этом на каждом шаге выбирается та вершина, для которой значение функции является наибольшим. Если на некотором шаге будет получен план, имеющий целочисленные компоненты, и значение функции на нем окажется больше или равно, чем значение в других возможных для ветвления вершинах, то данный план является оптимальным планом исходной задачи линейного целочисленного программирования и значение целевой функции на нем является максимальным.

X ₀

X_I ⁽¹⁾ X_II ⁽¹⁾

X_I ⁽²⁾ X_II ⁽²⁾

X_I ⁽³⁾ X_II ⁽³⁾

Рис. 5

ЛИТЕРАТУРА

1. Акулич И.Л. Математическое программирование в примерах и задчах: Учебное пособие. – М.: Высшая школа, 1993.

2. Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.: Наука, 1980.

3. Зайченко Ю.П. Исследование операций. – Киев: Вища школа, 1975.

4. Линейное и нелинейное программирование /Под общ. ред. проф. И.Н. Ляшенко. – Киев: Вища школа, 1975.

ОГЛАВЛЕНИЕ

Введение ………………………………………………………………………..…….3
Глава 1.	Понятия и принципы исследования операций
1.1.	Основные понятия и принципы исследования операций ….…….……4
1.2.	Математические модели операций …………………………..…………6
1.3.	Основные этапы операционного исследования ……………………….6
1.4.	Типичные классы задач …………………………………………………8
1.5.	Прямые и обратные задачи исследования операций. Детермини- рованные задачи ………………………………………………………..10
1.6.	Критерии эффективности ……………………………………………...12
Глава 2.	Линейное программирование
2.1.	Постановка основной задачи линейного программирования ……….17
2.2.	Существование решения ОЗЛП ……………………………………….19
2.3.	Геометрическая интерпретация ОЗЛП ……………………………….21
2.4.	Симплекс-метод решения ОЗЛП ……………………………………...
2.4.1.	Суть симплекс-метода ……………………..…………………………..25
2.4.2.	Табличный алгоритм замены базисных переменных …..……………26
2.4.3.	Нахождение опорного решения …………………….…………………28
2.4.4.	Определение оптимального решения …………………………………29
2.5.	Двойственная задача линейного программирования ………………...29
2.6.	Транспортная задача …………………………………………………...31
2.6.1.	Формулировка транспортной задачи ………………………………….33
2.6.2.	Нахождение опорного решения ……………………………………….34
2.6.3.	Нахождение оптимального решения ………………………………….36
2.6.4.	Транспортная задача с неправильным балансом …………………….38
2.7.	Целочисленное программирование …………………………………...39
Литература ………………………………………………………………………….42

Плотникова Наталья Валерьевна

ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

Дата добавления: 2019-02-12; просмотров: 234; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 56

Мы поможем в написании ваших работ!