НЕКОТОРЫЕ АЛГЕБРАИЧЕСКИЕ ВОПРОСЫ, СВЯЗАННЫЕ С ПОСТРОЕНИЕМ БОЛЬШИХ ПРОСТЫХ ЧИСЕЛ И РЕШЕНИЕМ УРАВНЕНИЙ В КОНЕЧНЫХ ПОЛЯХ

⇐ ПредыдущаяСтр 6 из 7Следующая ⇒

Как известно, одна из наиболее популярных криптосистем с открытым ключом - именно система RSA - требует для своей реализации выбора больших простых чисел. На практике это можно реализовать следующим образом. Берется случайным образом из некоторого интервала [A, B] целое число “x” и подвергается определенной процедуре проверки на простоту. Эта процедура должна заключаться в выявлении у числа “x” свойства (или некоторого множества свойств), присущего простым числам.

Пусть m - нечетное целое число и (w, m)=1. Если m - простое, то

w^m-1 º 1 (mod m) (5.1)

Соотношение (5.1) носит название малой теоремы Ферма.

Если m не является простым и (5.1) выполнено, то число m называется псевдопростым по основанию w .

Назовем целое число w, (w,m)=1, для которого выполнено (5.1) индикатором простоты числа m.

Утверждение 1. Все или не более половины целых чисел w, 1£w<m, (w,m)=1, являются индикаторами простоты m.

Доказательство. Пусть w_i, 1£i£t, - все индикаторы простоты для m. Пусть w не является индикатором простоты. Тогда числа

u_i = w×w_i (mod m), i = 1,2…,t,

попарно различны и ни одно из них не является индикатором простоты. При этом существует столько же чисел u_i, сколько всех индикатором простоты.

Однако малая теорема Ферма не может в полной мере решить нашу задачу хотя бы потому, что существуют такие составные числа “n”, для которых нет ни одного индикатора непростоты (числа Кармишеля).

Известно, что число Кармишеля не может быть квадратом другого числа. Известно также, что нечетное составное число m, не являющееся квадратом, есть число Кармишеля тогда и только тогда, когда для простого p, делящего m, p-1 делит m-1.

Наименьшее число Кармишеля равно m = 561 = 3·11·17.

Числами Кармишеля являются также все числа вида

(6i+1)(12i+1)(18i+1),

где все три множителя являются простыми числами.

Однако полного описания всех чисел Кармишеля нет.

Более удобной представляется в этом плане теорема Миллера.

Теорема 1 (Миллер).

Если n = p - простое и n-1 = r×2^k , где r - нечетно, тогда для любого целого a Î {1,2,...,n-1}

a^r º 1 (mod n)

или для некоторого i Î {0,1,...,k-1}

r×2ⁱ

a º -1 (mod n).

Утверждение 2 (Шамир). При нечетном составном n и случайном выборе числа aÎ{2,3,…,n-1} пара (n,a) будет удовлетворять теореме Миллера с вероятностью < .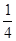

Другими словами, если n - нечетное составное число, то более чем три четверти целых чисел из интервала [2, n-1] являются индикаторами непростоты (относительно теоремы Миллера) для n.

Таким образом, если t независимых попыток нахождения индикатора в множестве {2,3,...,n-1} для числа n не привели к успеху, то число n является простым с вероятностью > 1-4^-^t.

Отметим, что в предположении справедливости расширенной гипотезы Римана теорема Миллера дает детерминированный полиномиальный алгоритм проверки на простоту, ибо в этом случае при нечетном составном n индикатор непростоты для “n” обязательно нашелся бы среди чисел множества {2, 3, ... , [2×log n]²}.

Для произвольного числа aÎZ и простого p символ Лежандра (a/p) определяется следующим образом :

ì 1, если уравнение x²=a имеет ненулевое решение в поле Z_p

(a/p) = í -1, если решений нет

î 0, если p делит a

Если (a/p)=1, то “a” называется квадратичным вычетом по модулю p, а если (a/p)=-1, то “a” - квадратичный невычет.

Утверждение 3. Если m - простое, то для всех целых w

w⁽^m^-1)/2 º (w/m) (mod m) (5.2)

Равенство (5.2) носит название формулы Эйлера.

Кроме того, символ Лежандра обладает следующими свойствами.

Утверждение 4.

1) (ab/p) = (a/p)(b/p);

2) (-1/p) = (-1)^(p-1)/2;

3) (a²/p) = 1;

4) (2/p) = (-1)^t, t=(p²-1)/8.

Теорема 2. (квадратичный закон взаимности Гаусса). Пусть n и p - различные нечетные простые числа. Тогда

(p/n)×(n/p) = (-1)^(n-1)(p-1)/4.

Пусть n=p₁^t(1)×p₂^t(2)×…×p_s^t(s) – разложение числа n в произведение ненулевых степеней различных простых чисел. Тогда символ Якоби (a/n) целого числа a по модулю натурального n определяется через соответствующие символы Лежандра следующим образом:

(a/n)=(a/p₁)^t(1)×(a/p₂)^t(2)×…×(a/p_s)^t(s).

Отметим, что аналоги приведенным выше утверждению 4 и теореме 2 будут справедливыми и применительно к символу Якоби (a/n), что позволяет эффективно вычислять символ Якоби (a/n) без разложения чисел "a" и "n" на простые множители.

На свойствах символа Якоби основан тест, называемый тестом проверки простоты Соловья-Штрассена.

Утверждение 5. Если m - нечетное составное число, то не более половины целых чисел w, где (w,m)=1, 1£w<m, удовлетворяют условию (5.2).

Доказательство. Покажем, что всегда существует w‘ такое, что соотношение (5.2) не выполняется для w=w‘.

Пусть p² делит m, где p - простое. Тогда полагаем w‘=1+m/p.

Теперь (w‘/m)=1, но левая часть соотношения (5.2) не может равняться 1 по модулю p, так как p не делит (m-1)/2.

Пусть теперь m - произведение различных простых чисел и p - одно из них. Выберем любой квадратичный невычет s по модулю p и пусть w‘, 1£w‘<m, такое, что

w‘ º s (mod p), w‘ º 1 (mod m/p).

Такое w‘ может быть найдено в силу взаимной простоты p и m/p. Тогда (w‘/m)=-1 и одновременно (w‘)^(m-1)/2º1 (mod m/p), Þ

(w‘)^(m-1)/2¹ 1 (mod m).

Далее следуют рассуждения как и при доказательстве утверждения 1. На этом доказательство закончено.

Рассмотрим теперь задачу нахождения корней заданного многочлена ¦ÎF_q[x] в поле F_q.

Ясно, что каждый алгоритм разложения многочлена ¦ÎF_q[x] может служить и алгоритмом нахождения его корней в поле F_q, так как корни отвечают линейным сомножителям канонического разложения ¦ в кольце F_q[x].

В качестве исходного шага при этом целесообразно выделить ту часть многочлена ¦, которая содержит все его корни в поле F_q. Это достигается вычислением НОД(¦(x), x^q-x) ввиду того, что двучлен x^q-x является произведением всех нормированных линейных многочленов кольца F_q[x].

Алгоритм 1 (вероятностный алгоритм нахождения корней заданного многочлена fÎF_p[x] в простом поле F_p).

Итак, рассматриваем многочлены fÎF_p[x], представимые в виде

¦(x) = 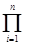(x-c_i),

где c₁,...,c_n - различные элементы поля F_p, p - простое число. Если p мало, то корни многочлена ¦ можно найти вычислением всех значений ¦(0), ¦(1), ... , ¦(p-1).

Пусть теперь p - большое простое нечетное число, bÎF_p.

Рассмотрим равенство

¦(x-b) = 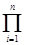(x - (b+c_i)).

Многочлен ¦(x-b) делит двучлен x^p-x = x×(x^(p-1)/2 +1)×(x ^(p-1)/2 -1). Если при этом x является делителем для ¦(x-b), то ¦(-b)=0, и найден один из корней многочлена ¦. В противном случае будем иметь

¦(x-b) = НОД(¦(x-b), x^(p-1)/2 +1)×НОД(¦(x-b), x^(p-1)/2 -1) (5.3)

После приведения многочлена x^(p-1)/2 по модулю ¦(x-b) в случае x^(p-1)/2¹±1 (mod ¦(x-b)) равенство (5.3) дает нетривиальное частичное разложение многочлена ¦(x-b). После замены x на x+b получаем частичное разложение и для многочлена ¦(x).

Если же x^(p-1)/2º±1 (mod ¦(x-b)), то выбираем другое значение bÎF_p.

В условиях определенной теоретико-вероятностной модели показано, что при случайном выборе bÎF_p среднее число попыток до получения неравенства x^(p-1)/2¹±1 (mod ¦(x-b)) равно 2.

При deg(f)=2 для нахождения корней многочлена f(x) в поле GF(q) в некоторых случаях существуют и более простые подходы, основанные на свойствах квадратичных вычетов.

Утверждение 6. В поле GF(q) при нечетном q уравнение x²=a имеет решение в том и только том случае, если a^(q-1)/2=1.

Доказательство. Пусть x=g^t, a=g^r, где g – примитивный элемент поля. Тогда g^2t=g^r, откуда получаем, что 2t-r=0 (mod q-1). Следовательно, r – четное число, и a^(q-1)/2=g^(q-1)(r/2)=1. Утверждение доказано.

Отметим, что при несовместности уравнения x²=a (т.е. когда a – квадратичный невычет в поле GF(q)) величина a^(q-1)/2 будет равна минус единице.

Утверждение 7. В поле GF(q) при q=3 (mod 4) корнями уравнения x²=a (в случае его совместности) являются величины x=±a^(q+1)/4.

Справедливость данного утверждения вытекает из равенств

x²=a^(q+1)/2=a×a^(q-1)/2=a×1=a.

В заключение отметим, что нахождение корней многочлена второй степени общего вида x²+bx+c над полем GF(q) нечетной характеристики сводится к уравнению вида x²=a.

МЕТОДЫ ФАКТОРИЗАЦИИ ЧИСЕЛ

Задача разложения на простые множители заданного нечетного составного числа “n” имеет важное прикладное значение для оценки криптографических качеств системы RSA.

Мы изложим здесь основные идеи одного из наиболее эффективных методов разложения - метода квадратичного решета (qs - метод), предложенного Померансом. Сложность этого метода составляет

L(n) = exp {(1+o(1))×(log n ×loglog n)^1/2} .

Пусть имеется пара целых чисел X, Y таких, что

X² º Y² (mod n). (6.1)

Тогда n является делителем числа (X - Y)×(X + Y).

Если p, q - различные простые делители для “n”, тогда с вероятностью 1/2 число X - Y делится на p, но не делится на q или делится на q, но не делится на p, т.е. d = НОД(X-Y, n) является нетривиальным делителем числа n.

Данные рассуждения свидетельствуют о том, что построение достаточно эффективного алгоритма нахождения решений сравнения (6.1) позволит с большой вероятностью разложить число n на множители.

Рассмотрим полином второй степени с целыми коэффициентами

¦(x) = (x + [n¹^/2])² - n (6.2)

Если x Î Z - целое число, тогда

(x + [n^1/2])² º ¦(x) (mod n).

Предположим, найдены различные целые x₁, x₂, ... , x_kтакие, что произведение ¦(x₁)×¦(x₂)×... ×¦(x_k) является квадратом, т.е.

¦(x₁)×¦(x₂)× ...×¦(x_k) = Y² .

Тогда для X = (x₁+ [n^1/2])× ... × (x_k+ [n^1/2]) получим равенство

X² º Y² (mod n),

т.е. получаем решение сравнения (6.1).

Таким образом, qs - метод заключается в сведении проблемы разложения числа n к поиску множеств x₁, x₂, ... , x_k различных целых чисел таких, что произведение ¦(x₁)×¦(x₂)×...×¦(x_k) является полным квадратом.

Заметим далее, что если ¦(x) имеет очень большой простой делитель, то, как представляется, будет очень трудно дополнить число x до нужной последовательности x₁, x₂, ... , x_k, ибо для этого нужно найти еще одно число x' такое, что ¦(x') имеет такой же простой делитель.

Эти соображения свидетельствуют о том, что следует избегать чисел ¦(x), обладающих большими простыми делителями.

Пусть p₁, p₂, ... , p_B - набор первых B простых чисел и x(1), x(2), ... , x(B+x) - целые числа такие, что

¦(x(i)) = 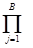p_j^a^(j,i), 1 £ i £ B+x,

где a(j,i) - неотрицательные целые числа.

Для каждого i рассмотрим двоичный вектор

v^®(i) = (a(1,i), ... , a(B,i)) (mod 2), 1 £ i £ B+x.

Так как среди векторов v^®(1), ... , v^®(B+x) может быть не больше B линейно независимых (рассматриваемых как векторы векторного пространства размерности B над полем из 2 элементов), то найдутся по крайней мере x соотношений вида

v^®(i(1)) + ... + v^®(i(k)) = 0 (mod 2),

каждое из которых показывает, что произведение

¦(x(i(1)))× ...× ¦(x(i(k))) = 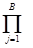p_j^S^a^(j,i),

является квадратом соответствующего числа (для фиксированного j суммирование в выражении Sa(j,i) проводится по всем iÎ{i(1),i(2),…,i(k)}).

Таким образом, будут найдены по крайней мере x решений сравнения (6.1). В предположении, что каждое из этих решений независимо друг от друга приводит к разложению n с вероятностью 1/2, получим разложение n с вероятностью 1-2 ^-^x .

Итак, мы приходим к задаче нахождения целых чисел x таких, что ¦(x) разложимо с помощью первых B простых чисел (будем в этом случае говорить, что ¦ (x) обладает свойством B - гладкости).

Далее изложим идею, позволяющую найти все нужные нам x (при которых ¦(x) обладает свойством B–гладкости) среди T последовательных чисел за 8B + 2T + 4T× loglog B сравнительно простых операций.

При T >> B это означает, что в среднем на каждое значение x из этого интервала приходится 2 + 4 loglog B операций.

Так как ¦(x) - полином с целыми коэффициентами, то из равенства

a º b (mod p) следует равенство ¦(a) º ¦(b) (mod p).

Следовательно, для нахождения всех целых x, для которых p|¦(x), достаточно решить квадратное уравнение

¦(x) º 0 (mod p) (6.3)

при x Î {0,1,...,p-1}.

Из вида (6.2) многочлена ¦(x) следует, что если p > 2 и p не делит n, тогда уравнение (6.3) имеет два различных решения a₁, a₂(mod p), если n является квадратом по модулю p (т.е. если символ Лежандра (n/p) равен 1), и не имеет ни одного решения в противном случае.

Отсюда следует, что простые p такие, что (n/p) = -1 не могут быть делителями ¦(x) ни при каких “x”. Поэтому мы будем под “первыми B простыми числами” понимать первые B простые числа p, для которых (n/p) = 1 (либо p = 2).

Множество этих чисел назовем “базой” (предположительно база будет состоять из случайного набора B чисел из множества 2×B первых простых чисел).

Для каждого из первых B простых чисел p со свойством (n/p) = 1 находим решения уравнения (6.3) в множестве {0,...,p-1}. Обозначим их через a₁_p, a₂_p . Далее для каждого “x” из выбранного промежутка последовательных чисел длины T выделяем [log₂¦(x)] и запоминаем результат в ячейке памяти с адресом x.

Число [log₂¦(x)] есть число бит в двоичном представлении и остается постоянным для больших интервалов последовательных значений “x”.

Далее для каждого нашего простого p мы вычитаем [log₂p] из числа, находящегося по адресу x, если и только если

x º a_1p (mod p) или xºa_2p (mod p).

Эти адреса образуют две арифметические прогрессии с шагом p и, следовательно, могут быть вычислены за 2 +(2T/p) сложений числа p к предыдущим адресам. Кроме того, столько же необходимо операций вычитания числа [log₂ p]. Следовательно, общее число арифметических операций составит 4 + (4T/p). Учитывая далее операции чтения и записи чисел в память, получим в итоге

å (8 + 8T/p) » 8B + 4T×loglog B

операций, из которых половина арифметические, а другая половина - обращение к памяти.

При этом предполагалось, что для случайных B простых чисел из первых 2×B простых чисел справедливо

å 1/p @ 1/2 ( log log B ) .

В результате такой процедуры, если число x является для нас искомым (т.е. ¦(x) обладает B - гладкостью), то по адресу x будет находиться целое число, близкое к нулю. Строго говоря, там будет находиться число

[log₂ ¦(x)] - ( 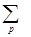[log₂ p]) ,

где суммирование ведется по всем простым p из “базы”.

Просмотрев итоговый массив памяти и выделив адреса x, по которым записано число, “близкое” к нулю, мы получим если не все, то значительную часть нужных нам чисел x.

Учитывая, что для начального формирования массива и конечного его просмотра нужно по T шагов, итоговая сложность составит

8B + 2T + 4T×log log B

операций.

В следующей таблице приведены оценки для числа “успешных” чисел в зависимости от рассматриваемого интервала длины T.

интервал для x	ожидаемое число “успехов”
[1, 10⁹]	< 1
[10⁹, 10¹⁰]	4
[10¹¹, 10¹²]	131
[10¹³, 10¹⁴]	4050
[10¹⁵, 5×10¹⁵]	65000

Отметим, что среднее число попыток для получения B «успешных» чисел x равно B×p^-1, где p – вероятность B - гладкости числа ¦(x) при случайном выборе x. При этом величина Q=B×p^-1 может служить оценкой сложности соответствующего алгоритма факторизации.

Качественная оценка вероятности B-гладкости случайного числа из промежутка длины T задается выражением p=l^-^l, l» .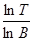

Пример. Если n»10¹²⁰, x»n^d , d > 0 - мало, то ¦(x) » n^1/2 = 10⁶⁰ .

Если при этом B = 10⁵, то вероятность B - гладкости случайного числа ¦(x) составляет » 10^-10, и Q=B×p^-1=10¹⁵.

НЕКОТОРЫЕ ВОПРОСЫ,

Дата добавления: 2019-02-12; просмотров: 161; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒

Мы поможем в написании ваших работ!