По данной системе цифровой подписи
1. Предложенная схема ЭЦП может работать не только в случае поля GF(p), но и при произвольном конечном поле GF(q). Однако считается, что проблема логарифмирования в простом поле решается труднее, чем в полях GF(pm), m > 1.
2. Сложность логарифмирования в простом поле GF(p) приблизительно такова же, что и сложность разложения на множители числа “n” при log p = log n. Поэтому и криптографические качества схем ЭЦП, основанных на этих математических проблемах, также примерно одинаковые.
3. При вычислении подписи (в соотношении 3.4.1) вместо открытого сообщения m целесообразно использовать его свертку h=H(m) с помощью хэш-функции H. Это защищает от возможности подбора сообщений с известным значением подписи.
4. ЭЦП Эль-Гамаля послужила образцом для построения целого семейства схем подписи в том числе стандартов цифровой подписи США и России. В их основе лежит проверка сравнения
aA×yB=rC (mod p),
в котором тройка (A,B,C) совпадает с одной из перестановок чисел (±m, ±s, ±r). Так исходная схема Эль-Гамаля получается при A=m, B=-r, C=s. В стандарте США Digital Signature Standard (DSS) использованы значения A=m, B=r, C=s, а в стандарте ГОСТ Р 3410-2001 ¾ A=-m, B=s, C=r.
5. В указанном семействе схем цифровой подписи можно вместо пары (r,s) использовать пару (r (mod q), s (mod q)), где q – простой делитель числа p-1. При этом исходное проверочное равенство заменяется на модифицированное
(aA×yB (mod p))=rC (mod q).
|
|
|
Схема цифровой подписи Диффи-Лампорта на основе симметричных систем шифрования
Схемы цифровой подписи (а равно и шифрования), основанные на сложности решения известных математических задач, имеют потенциальный недостаток, заключающийся в возможности построения новых эффективных алгоритмов решения соответствующих математических задач. Поэтому в таких схемах длину ключа стремятся выбирать с определенным превышением необходимой длины, обеспечивая запас криптографической стойкости. Это, в свою очередь, приводит к усложнению (уменьшению скорости работы) алгоритмов вычисления и проверки подписи.
В этой связи представляет интерес задача построения схем ЭЦП на основе симметричных криптографических систем, свободных от подобных недостатков.
Пусть требуется подписать сообщение M=m(1),m(2),…,m(n), m(i)Î{0,1}.
В схеме Диффи-Лампорта подписывающий выполняет следующие действия.
1. Выбирает 2n случайных секретных ключей K={(k10,k11),…,(kn0,kn1)} для используемой им симметричной криптосистемы.
2. Выбирает n пар случайных чисел S={(s10,s11),…,(sn0,sn1)}, sijÎ{0,1}.
3. Вычисляет значения rij=Ek(i,j)(sij), где Ek(i,j)(sij) – алгоритм шифрования сообщения sij на ключе kij.
4. Наборы S={(s10,s11),…,(sn0,sn1)} и R={(r10,r11),…,(rn0,rn1)} помещаются в общедоступный справочник. При этом помещать информацию в такой справочник может только автор подписи.
|
|
|
5. Подпись для сообщения M имеет вид (k1m(1),…,knm(n)).
Критерием правильности подписи является выполнение равенств
rij=Ek(i,j)(sij), j=m(i), i=1,2,…,n.
Одним из недостатков данной схемы является значительный объем цифровой подписи, которая может превышать само подписываемое сообщение. Для его устранения можно хранить единственный секретный ключ k, из которого формировать последовательность K: kij=Ek(i,j), i=1,2,…,n, j=0,1.
Основной же недостаток схемы цифровой подписи Диффи-Лампорта состоит в том, что после проверки подписи часть ключевого множества K становится известной проверяющему. Поэтому данная схема подписи является по существу одноразовой.
Отметим также, что в схеме Диффи-Лампорта нельзя использовать симметричные криптосистемы, «слабые» относительно атаки по известным открытому и шифрованному текстам, например, шифр наложения ключевой гаммы: rij=sij+kij (mod 2). Использование таких криптосистем привело бы к восстановлению ключевой последовательности K={(k10,k11),…,(kn0,kn1)} по известным наборам S={(s10,s11),…,(sn0,sn1)} и R={(r10,r11),…,(rn0,rn1)}.
|
|
|
ЛОГАРИФМИРОВАНИЕ В КОНЕЧНЫХ ПОЛЯХ
Методы логарифмирования для произвольной циклической группы
Мы будем рассматривать задачу логарифмирования применительно к произвольной циклической группе G = <g> порядка çGç=n, порожденной образующим элементом “g”, т.е. нас интересует решение уравнения
gx = b
при заданных g и b Î G.
Отметим, что в рассматриваемую нами схему вкладывается и случай логарифмирования в конечных полях GF(q), ибо множество ненулевых элементов поля GF(q) образует циклическую группу относительно операции умножения.
Отправной точкой к оценке сложности задачи логарифмирования будет служить
Метод 1 (полное опробование).
Суть данного метода состоит в вычислении таблицы логарифмов для всех элементов группы G, после чего логарифм конкретного элемента bÎG получается в результате просмотра данной таблицы.
Данный метод требует O(n) операции для вычисления таблицы. Кроме того, необходимо O(n) ячеек памяти для хранения таблицы.
Метод 2 (метод Шенкса).
Данный метод имеет сложность O(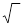 
n×logn) операций и требует память для хранения O( 
n) элементов группы. Существо данного метода заключается в следующем.
|
|
|
Пусть ¦: G ® {1,2,...,n}- некоторое инъективное отображение группы G на множество {1,2,...,n}.
Заметим, что логарифм любого элемента группы G можно записать в виде mq - r, где
m = [ n], 0 £ r £ m, 0 £ q £ m.
Поэтому для вычисления логарифма элемента b Î G достаточно найти соответствующие q и r.
Построим два множества
S = { (i, ¦(bgi)) , i = 0,...,m}
T = { (i, ¦(gmi)) , i = 0,...,m}.
Произведем сортировку множеств S и T по второй координате и затем найдем s Î S и t Î T такие, что у них вторые координаты совпадают.
Это дает нам уравнение
bgr = gmq ,
отсюда
b = g mq-r .
Осталось заметить, что наиболее сложным в данном методе является этап сортировки, который требует O(m×log m) операций.
Метод 3 (метод Полига-Хеллмана-Сильвера).
Назовем целое число y - “гладким”, если оно не имеет простых делителей, превосходящих числа “y”.
Пусть n =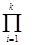 
pic(i) , p1 < ... < pk, - разложение числа n по степеням различных простых множителей.
Рассмотрим уравнение gx = a при заданных g и a Î G, çGç=n.
Идея нахождения логарифма элемента aÎG будет заключаться в нахождении величины log a (mod pic(i)), i = 1,2,...,k, что с учетом китайской теоремы об остатках будет равносильно нахождению log a (mod n), т.е. решению стоящей задачи.
Для простоты обозначений положим p - простое число такое, что
pc | n и pc+1 не делит n, x = log a (mod pc ). Ясно, что “x” может быть представлено в виде
x =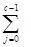 
bj pj , 0 £ bj < p.
Заметим, что log a = x + pc t для некоторого целого t, следовательно,
c-1
nx/p+npc-1t n å bj pj-1 nb0/p
an/p = g = g j=0 = g .
Теперь для вычисления b0 мы вычисляем an/p и x = gn/p . Далее вычисляем xi для i = 0,1,...,p-1 до тех пор, пока не получим равенство xi = an/p . Найденное значение i и будет b0 .
Если c > 1, то для нахождения b1 (после того, как b0 найдено) действуем следующим образом.
Пусть h = g-1= gn-1 , b(0)=b0, a1 = a×hb(0). Тогда
c-1
n/p2 n å bj pj-2 b1
a1 = g j=1 = x .
Перебирая i = 0,1,...,p-1, находим i = b1 такое, что
n/p2
xi = a1 .
Аналогичным образом находятся и остальные величины среди b0, b1, ... , bc-1.
Сложность вычисления логарифмов данным методом оценивается величиной
O ( 
ci × (log n + pi)).
Если же в данном методе использовать и идею метода Шенкса (на этапах, когда ищется i Î {0,1,...,p-1} такое, что xi равно заданному элементу), то сложность будет
O (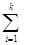 
ci × (log n + pi 1/2 ×log pi)).
Однако при этом потребуется память порядка O(pk1/2) для записи элементов группы.
4.2. Субэкспоненциальные методы логарифмирования в конечных полях (методы Адлемана, “Ватерлоо”, Копперсмита для случая поля GF(2n))
Ниже приведем несколько алгоритмов дискретного логарифмирования, имеющих субэкспоненциальную сложность. При этом мы ограничимся случаем поля GF(2n) (для простоты изложения), хотя некоторые из этих методов справедливы и в более общем случае. Поле GF(2n) мы будем представлять полем многочленов степени £ n-1 над полем GF(2) по модулю заданного неприводимого многочлена степени “n”
Алгоритм Адлемана
Данный алгоритм состоит из двух частей. Первая часть заключается в вычислении множества базовых логарифмов. Вторая часть состоит в вычислении конкретного логарифма.
Часть первая.
Вычисляем логарифмы всех неприводимых многочленов степени не более “b”, где b - фиксированное натуральное число, выбираемое в зависимости от поля GF(2n) и являющееся параметром метода.
Часть вторая.
Для нахождения логарифма заданного ненулевого элемента g(x)ÎGF(2n), генерируем случайное целое число “m” и вычисляем (в поле GF(2n))
h(x) = g(x) am (x),
где a(x) - образующий многочлен поля GF(2n).
Разложим h(x) на неприводимые множители
h(x) =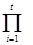 
pie(i)(x).
Если deg pi (x) £ b при всех i, 1 £ i £ t, тогда
log g(x) =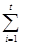 
e(i) log pi (x) - a (mod 2n-1).
А так как логарифмы элементов pi(x) находятся в базе данных, то задачу вычисления логарифма для данного элемента g(x) можно считать решенной.
Если же не все pi (x) имеют степень £ b, то выбираем другое целое “m” и повторяем попытку.
Через N(n,b) обозначим число многочленов степени “n” таких, что разложение любого из них на неприводимые факторы содержит только многочлены степени £ b. Тогда вероятность p(n,b) попадания на элемент из множества N(n,b) при случайном выборе многочлена степени “n” составит
p(n,b) =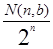 
.
Поэтому при вычислении логарифма конкретного элемента g(x) потребуется в среднем p(n,b)-1 раз использовать часть 2 излагаемого алгоритма.
Известно, что
p(n, b) » 
-(1+o(1))n/b .
и асимптотическое время работы алгоритма составляет
¾--------------
exp (c1Ö n log n ).
Пусть S - множество всех неприводимых многочленов степени £ b. Для нахождения логарифмов всех элементов множества S мы можем образовать систему линейных уравнений, в которой неизвестными являются искомые логарифмы.
Эта система уравнений образуется путем применения части 2 алгоритма к каждому элементу множества S. Полученная система из |S| уравнений с |S| неизвестными далее решается в кольце вычетов по модулю 2n-1.
Число применений части 2 алгоритма для получения всех |S| уравнений составит в среднем |S|×p(n,b)-1.
В качестве примера рассмотрим случай поля GF(2127). В этом случае величина |S|×p(n,b)-1 минимизируется при b = 23.
При этом число неприводимых многочленов степени £ 23 равно 766150. Следовательно, для получения логарифмов всех этих многочленов необходимо получить и решить систему из 766150 линейных уравнений от 766150 неизвестных.
Отметим далее, что случайный многочлен степени £ 126 разлагается на неприводимые факторы из базового множества S при b = 23 с вероятностью 0.000138. Таким образом, для получения требуемого числа линейных уравнений потребуется порядка 5,55×109 итераций части 2 алгоритма.
2. Алгоритм “Ватерлоо”
Данный алгоритм имеет два отличия от изложенного выше алгоритма.
Суть первого отличия.
К многочленам h(x) = g(x)am(x) и ¦(x) (напомним, что ¦(x) - неприводимый многочлен, задающий поле GF(2n)) применяем расширенный алгоритм Евклида и находим пару многочленов
s(x), t(x), (s(x), t(x)) = 1,
deg s(x) £ n/2, deg t(x) £ n/2 ,
таких, что
h(x) t(x) = s(x) (mod ¦(x)) .
Если при этом оба многочлена s(x) и t(x) окажутся S - гладкими (т.е. разложимыми на многочлены из множества S), тогда log g(x) легко вычисляется на основе имеющейся базы данных.
Преимущество данного шага в том, что вероятность S - гладкости двух случайно выбранных полиномов степени £ n/2 выше, чем одного полинома степени “n”.
Через N(b,i,j) обозначим число пар взаимно простых полиномов (A(x),B(x)) , deg A(x) = i, deg B(x) = j, каждый из которых обладает свойством S - гладкости (напомним, что множество S состоит из всех неприводимых многочленов степени £ b).
Вероятность того, что упорядоченная пара взаимно простых полиномов (A(x),B(x)), степени которых £ n/2, обладает свойством S - гладкости будет выражаться величиной
p* (n,b) = { å N(b,i,j) }×2-n.
0£i, j£n/2
В качественном отношении величину p* (n,b) можно приближать величиной [p(n/2,b)]2 .
К примеру, при n =127, b = 17 имеем:
p* (127, 17) » 1/7000, [p(63, 17)]2 » 1/5000 .
Следующая таблица дает сравнительную характеристику алгоритмов Адлемана и “Ватерлоо” при n = 127:
| b | |S| | p* (n,b) | |S|×p* (n,b)-1 | p(n,b) | |S|×p(n,b)-1 |
| 1 | 1 | 1.27×10-32 | 7.87×1031 | 0.48×10-34 | 0.21×1035 |
| 2 | 2 | 1.61×10-30 | 1.24×1030 | 0.1×10-32 | 0.19×1034 |
| 3 | 4 | 1.42×10-27 | 2.82×1027 | 0.11×10-30 | 0.37×1032 |
| 4 | 7 | 1.15×10-24 | 6.07×1024 | 0.16×10-28 | 0.44×1030 |
| 5 | 13 | 3.46×10-21 | 3.75×1021 | 0.13×10-25 | 0.1×1028 |
| 6 | 22 | 2.43×10-18 | 9.05×1018 | 0.6×10-23 | 0.36×1025 |
| 7 | 40 | 1.75×10-15 | 2.29×1016 | 0.59×10-20 | 0.68×1022 |
| 8 | 70 | 2.99×10-13 | 2.34×1014 | 0.2×10-17 | 0.34×1020 |
| 9 | 126 | 2.39×10-11 | 5.26×1012 | 0.4×10-15 | 0.31×1018 |
| 10 | 225 | 7.73×10-10 | 2.91×1011 | 0.32×10-13 | 0.71×1016 |
| 11 | 411 | 1.43×10-8 | 2.88×1010 | 0.14×10-11 | 0.3×1015 |
| 12 | 746 | 1.48×10-7 | 5.04×109 | 0.3×10-10 | 0.25×1014 |
| 13 | 1376 | 1.07×10-6 | 1.29×109 | 0.41×10-9 | 0.33×1013 |
| 14 | 2537 | 5.47×10-6 | 463887639 | 0.37×10-8 | 0.68×1012 |
| 15 | 4719 | 2.19×10-5 | 215451634 | 0.25×10-7 | 0.19×1012 |
| 16 | 8799 | 7.21×10-5 | 123548311 | 0.13×10-6 | 0.69×1011 |
| 17 | 16509 | 1.97×10-4 | 83945854 | 0.52×10-6 | 0.31×1011 |
| 18 | 31041 | 4.71×10-4 | 65902291 | 0.18×10-5 | 0.17×1011 |
| 19 | 58635 | 10-3 | 58190035 | 0.53×10-5 | 0.11×1011 |
| 20 | 111012 | 1.96×10-3 | 56563479 | 0.14×10-4 | 0.8×1010 |
| 21 | 210870 | 3.54×10-3 | 59537985 | 0.33×10-4 | 0.65×1010 |
| 22 | 401427 | 5.97×10-3 | 67283339 | 0.7×10-4 | 0.58×1010 |
| 23 | 766149 | 9.45×10-3 | 81044911 | 0.14×10-3 | 0.55×1010 |
| 24 | 1465019 | 0.14×10-1 | 103071637 | 2.26×10-3 | 0.57×1010 |
Суть второго отличия связана с получением уравнений для элементов базы данных. Получение некоторого количества таких уравнений может быть значительно ускорено с учетом линейности операций возведения в квадрат в поле GF(2n). Продемонстрируем это на основе поля GF(2127) и многочлена
¦(x) = x127 + x + 1.
Так как
x128 º x2 + x ( mod ¦(x)) ,
то легко видеть, что xt(i), t(i)=2i, 0£i£126, можно представить в форме
e =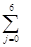 
gj×xt(j), t(j)=2j, gj Î{0,1}.
Тем самым логарифм любого элемента “e” можно легко вычислить. Это дает, в частности, 31 уравнение с максимальной степенью £ 16.
Еще один возможный способ в этом направлении заключается в следующем.
Пусть p(x) = xm + g(x), где deg (g(x)) = k << m. Через d обозначим наибольшее целое число такое, что 2d × m £ n.
Пусть s = n - 2d m, t(d)=2d и рассмотрим многочлен
L(x) = xs×p(x)t(d) (mod ¦(x)).
Тогда
deg L(x) £ max {k×2d + s, deg (¦(x) + xn)}.
Благоприятным для нас случаем является S - гладкость многочленов p(x) и L(x).
Например, при n = 127, ¦(x) = x127 + x + 1, положим p(x) = 1 + x7 .
Тогда d = 4, s = 15, и мы имеем
L(x) = x15 ×(1 + x7)16 = 1 + x + x15 .
Таким образом, L(x) и p(x) оказались гладкими для b = 15.
Аналогичного сорта результат может быть получен при
использовании многочлена p(x)t, t=2d+1.
3. Алгоритм Копперсмита
Данный алгоритм является наиболее эффективным для поля GF(2n) и заключается в следующем.
Часть первая алгоритма (заложение базы данных).
Для получения достаточного числа уравнений, задающих базу данных, берутся пары полиномов a(x), b(x) таких, что
deg a(x) £ d, deg b(x) £ d, (a(x),b(x)) = 1,
где d < b - некоторое число.
Пусть k - степень двойки, причем k » (n/d)1/2 .
Пусть далее h - наименьшее целое число, большее чем n/k.
Предположим также, что задающий поле GF(2n) полином имеет вид
¦(x) = xn + g(x),
где g(x) - многочлен “небольшой” степени.
Пусть h(x) = xhk = g(x) xhk-n и определим c(x) = xh a(x) + b(x) и
d(x) = [c(x)]k .
Смысл такой конструкции заключается в том, что степень нелинейности многочленов c(x) и d(x) становится ограниченной сверху
величиной порядка (nd)1/2 , что повышает вероятность их S - гладкости.
Более строго для степеней c(x) и d(x) будем иметь соотношения
deg c(x) £ h + d = 
+ d,
deg d(x) £ max {kd, deg (g(x) xhk-n )+k×deg(a(x))}.
В частности, при n = 127, k = 4, h = 32, d = 10 получим
deg c(x) £ 42, deg d(x) £ 42
(предполагаем, как обычно, что ¦(x) = x127 + x + 1).
Для c(x) и d(x) могут использоваться и другие (но близкие по смыслу) конструкции, жестко ограничивающие степень нелинейности получающихся полиномов.
Например, пусть для поля GF(2127 )
c(x) = a(x)×x31 + b(x), d(x) = x3 ×[c(x)]4 ,
где deg a(x) £ 7, deg b(x) £ 8.
Тогда deg c(x) £ 38, deg d(x) £ 35.
Если с(x) и d(x) будут S - гладкими, то мы получим линейное уравнение.
Часть вторая алгоритма (нахождение логарифма заданного элемента).
Пусть g(x)ÎGF(2n) - элемент поля GF(2n), который требуется прологарифмировать. Основная идея нахождения log g(x) заключается в сведении задачи к нахождению логарифмов некоторого множества многочленов степени меньшей, чем deg g(x).
Первый шаг в этом направлении уже сделан в алгоритме “Ватерлоо”, когда нахождение логарифма многочлена степени »n сводится к задаче логарифмирования двух многочленов степени £ n/2.
В методе Копперсмита далее задача сводится к логарифмированию
нескольких (не более n) полиномов степени (n×b)1/2 .
При этом используется описанная выше конструкция вида
c(x) = xh a(x) + b(x), d(x) = [c(x)]k
с соответствующим выбором параметров и так, чтобы многочлен c(x) делился на заданный многочлен F(x) (логарифм которого необходимо найти) и многочлены c(x)/F(x) и d(x) одновременно разлагались на неприводимые множители степени £ (nb)1/2.
Затем задача сводится к логарифмированию £ n2 многочленов
степени £ (bb')1/2, где b' = (nb)1/2 и так далее. В конечном итоге интересующие нас величины будут выражаться через логарифмы неприводимых многочленов степени £ b, т.е. базу данных.
Сложность алгоритма оценивается величиной
exp(c×n1/3 ×(log n)2/3).
Дата добавления: 2019-02-12; просмотров: 199; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!