Кинетическая энергия материальной точки и механическая работа
Второй закон Ньютона устанавливает связь между ускорением материальной точки и действующими на нее силами. Однако в ряде случаев бывает удобно освободиться от ускорения. Это можно сделать путем совместного использования уравнений кинематики и второго закона Ньютона. При этом появляются две новые физические величины, имеющие большое значение: механическая работа и кинетическая энергия.
Пусть материальная точка движется прямолинейно с ускорением а под действием силы, направленной в сторону движения тела. Из кинематики известно, что при переходе тела из одной точки в другую выполняется соотношение
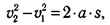
где v 2 и v 1 — конечная и начальная скорости тела; s — пройденный путь.
По второму закону Ньютона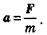 
Подставив в формулу, получим:
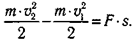
Можно показать, что в общем случае, когда сила образует с направлением движения угол а, формула принимает вид (рис. 4.3):
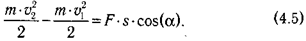
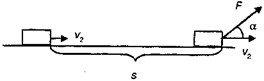
Рис. 4.3. Изменение кинетической энергии тела под действием силы
Скалярная величина, равная половине произведения массы тела на квадрат его скорости называется кинетической энергией тела:
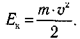(4.6)
Кинетическая энергия тела (от гр. kinetikos — приводящий в движение) — это энергия, которой тело обладает вследствие движения.
Скалярная величина, равная произведению силы, действующей на тело, на пройденный им путь и на косинус угла между направлением силы и направлением движения называется механической работой:
|
|
|
A = F·s·cos ( α ). (4.7)
Если на тело действует несколько сил ( FI , FII ...), то полная работа равна сумме работ отдельных сил:
А = АI+AII+...
Подставив формулы (4.6 и 4.7) в соотношение (4.5), получим связь между работой равнодействующей силы и кинетической энергией материальной точки.
Изменение кинетической энергии материальной точки равно сумме работ всех действующих на нее сил:
EК2 - EК1= АI+AII+... (4.8)
Здесь EК2 и EК1— кинетическая энергия тела в начальной и конечной точках траектории.
Это соотношение выполняется и в общем, случае, но работа вычисляется как интеграл от силы вдоль траектории движения от ее начальной точки (1) до конечной точки (2):
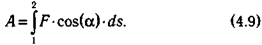
Работа силы может быть как положительной, так и отрицательной. Ее знак определяется величиной угла а. Если этот угол острый (сила направлена в сторону движения тела), то работа положительна. При тупом угле а работа отрицательна.
Если при движении точки угол α = 90° (сила направлена перпендикулярно вектору скорости), то работа равна нулю.
Пример
Пусть тело массой т, начальная скорость которого равна нулю, начинает двигаться по гладкой горизонтальной плоскости под действием силы F , направленной вдоль нее. Кроме силы F , на тело будут действовать еще две силы (рис. 4.4):
|
|
|
• сила притяжения (Fпр), направленная вниз;
• реакция опоры ( N ), действующая со стороны плоскости и направленная перпендикулярно ей.
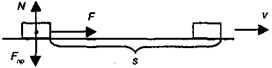
Рис. 4.4. Движение тела по гладкой плоскости
Требуется определить, какую скорость приобретет тело, пройдя путь s.
Применим к движению тела уравнение (4.8):
EК2 - EК1= Аf+Aпр+ Аf (4.10)
Начальная скорость равна нулю, поэтому Ек1 = 0. Конечную скорость обозначим v . Тогда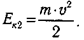 
Для силы F угол α = 0 и cos(α) = 1. Поэтому АF = F·s . Для сил Fnp и N угол α = 90° и соs(α) = 0. Поэтому их работы равны нулю. Подставив эти значения в (4.10), получим:
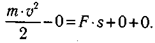
Отсюда найдем конечную скорость:
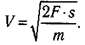
Дата добавления: 2019-01-14; просмотров: 209; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!