Характеристики движения тела, брошенного под углом к горизонту, по двум осям (ось Y направлена вверх)

⇐ ПредыдущаяСтр 15 из 100Следующая ⇒

Характеристики	Ось Х	Ось Y
Начальная скорость	v_0x = v₀·cos(θ₀)	v_0y ⁼ v₀∙ sin(θ₀).
Ускорение	0	— g
Время полета
Дальность полета для случая, когда точки броска и приземления находятся на одной высоте
Максимальная высота
Скорость в момент t	v_{x =}v_0x	v_{y =}v_0y—gt
Координаты в момент t	х = v_x . t	y = v_0y∙ t -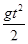

Максимальная высота подъема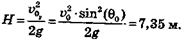

Полет пули

Из автомата производят выстрел в горизонтальном направлении ( q ₀ = 0). Начальная скорость пули v ₀ = 715м/с. Расстояние до мишени х = 100 м. В нашем случае v_x – v ₀ _x = v ₀ = 715 м/с; v ₀ _y = 0.

Из уравнения х = v_x∙t найдем t = = 0,14с Координата точки мишени, в которую попадет пуля, находится из уравнения y= v ₀ _y ∙t 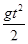= -0,1 м. Таким образом пуля опустится на 10 см. Чтобы скомпенсировать такое опускание, выстрел производят под небольшим углом вверх, для чего соответствующим образом устанавливают прицел.

Прыжок в длину с разбега (рис. 3.18)

Оценим теоретическую максимальную дальность прыжка в длину, определяемую физическими возможностями человека. Горизонтальную скорость v ₀ _x спортсмен набирает при разбеге.

Примем ее равной максимальной скорости спринтера: v ₀ _x = 10,5 м/с. Вертикальную скорость v₀ спортсмен приобретает при отталкивании. Оценим ее исходя из того, что высота, на которую человек может поднять свой центр масс, прыгая вертикально вверх с места, приблизительно равна 0,6 м. Из формулы

Рис. 3.18. К описанию прыжка в длину с разбега

Найдем v ₀ _y = 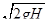= 3,43 м/с. Прыгун отталкивается в вертикальном положении, а приземляется в «сидячем» положении. При этом центр масс опускается приблизительно на 0,6 м (при отталкивании центр масс находится на высоте ~1 м, а при приземлении на высоте ~0,4 м). Значит координата точки приземления у -0,6 м.

Эта координата определяется формулой Подставив численные значения, получим квадратное уравнение: 4,9-t ² — 3,43∙t — 0,6 = 0. Решив его, найдем время полета t = 0,845 с. Дальность прыжка найдем из формулы s = v_x ∙ t = 8,87 м.

Движение по окружности, центростремительное и тангенциальное ускорения. Угловое ускорение

В природе движение тела чаще происходит по кривым линиям. Почти любое криволинейное движение можно представить как последовательность движений по дугам окружностей. В общем случае, при движении по окружности скорость тела изменяется как по величине, так и по направлению.

Равномерное движение по окружности

Движение по окружности называется равномерным, если величина скорости остается неизменной.

Основными характеристиками такого движения являются:

• радиус окружности R;

• скорость движения (линейная скорость) V ;

• угловая скорость движения ;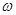

• угол поворота радиуса (угловое перемещение)

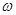
Угловой скоростьютела, движущегося по окружности равномерно, называется отношение угла поворота его радиус-вектора ко времени, за которое совершен поворот:

В физике применяется радианная мера угла (безразмерная), которая определяется, как отношение длины дуги (l) к радиусу

окружности: , поэтому размерность угловой скорости —

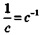, рис. 3.19, а. Радиан — такой угол, длина дуги которого равна радиусу окружности. Полный поворот по окружности содержит 2π радиан.

Рис. 3.19. Радианная мера угла (а). Центростремительное ускорение (б)

Между линейной и угловой скоростями существует простая связь:

Можно показать (рис. 3.19.6), что при равномерном движении по окружности вектор ускорения направлен к центру. Такое ускорение называется центростремительным.

Величина центростремительного ускорения определяется формулами

Кроме основных характеристик вращательного движения, используются следующие вспомогательные величины:

• частота вращения (v), равная числу оборотов за единицу

времени: (N — число оборотов). Размерность — 1 /с.

• период обращения (Т), равный времени, за которое тело совершает один оборот: . Размерность — с.

Эти величины связаны с угловой скоростью соотношениями:

Неравномерное движение по окружности

Если скорость тела, движущегося по окружности, изменяется по величине, то наряду с центростремительным ускорением а_цбудет иметь место и тангенциальное ускорение a_t, рис. 3.20.

Рис. 3.20. Компоненты ускорения при неравномерном вращательном движении

В отличие от центростремительного ускорения, которое обусловлено изменением направления скорости, тангенциальное ускорение возникает из-за изменения величины вектора скорости:

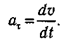
Тангенциальное ускорение всегда направлено по касательной к окружности, и, если скорость увеличивается, его направление совпадает с направлением движения. Если же скорость уменьшается, то направление тангенциального ускорения противоположно вектору скорости. Вектора а_ци а _τ перпендикулярны друг другу, а их сумма дает вектор полного ускорения:

а = а_ц + а_τ.

Поскольку эти векторы всегда перпендикулярны друг другу, величина полного ускорения в любой момент времени равна:

С тангенциальным ускорением мы встречаемся в спорте. Например, раскручивая молот, спортсмен сообщает ему тангенциальное ускорение для того, чтобы он приобрел к моменту броска высокую скорость.

Кроме обычного ускорения (а), при описании неравномерного движения по окружности используют еще одну характеристику — угловое ускорение (ε).

Угловым ускорением тела называется производная от угловой скорости по времени (отношение изменения угловой скорости ко времени этого изменения, вычисленное в очень маленьком интервале данной точки траектории):

(3.11)

Размерность ускорения в СИ — 1 /с².

Примечание. В тех случаях, когда угловая скорость рассматривается как вектор, угловое ускорение тоже является вектором. В данном учебнике такие случаи не рассматриваются.

Можно показать, что угловое ускорение равно отношению тангенциального ускорения к радиусу окружности:

Дата добавления: 2019-01-14; просмотров: 220; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

Мы поможем в написании ваших работ!