Применение законов динамики для анализа движений спортсменов
Разберем некоторые примеры, показывающие, каким образом законы динамики применяются для анализа сложных движений и вычисления сил, нагружающих суставы, сухожилия и мышцы.
На рис. 8.8. показан стартующий бегун. На него действуют сила тяжести mg и реакция опоры R , сообщающие центру масс бегуна ускорение а.

Воспользуемся неинерциальной системой отсчета, связанной с центром масс. В этой системе центр масс покоится. Согласно принципу ДАламбера к реальным силам следует добавить фиктивную силу инерции Fa = -т-а и записать условие покоя:
Эти уравнения можно использовать для решения двух задач:
• зная силы, действующие на тело, описать движение центра масс;
• зная ускорение тела (используя различные способы регистрации, например, киносъемку), определить вызвавшие его силы.
Вычислим силу тяги мышц F , нагружающих ахиллово сухожилие при старте бегуна. На рис. 8.9 показаны стопа и действующие на нее силы.


В проекциях на координатные оси это равенство запишется в виде системы двух уравнений:
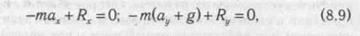
где Rx , R — составляющие реакции опоры; а и ах — вертикальная и горизонтальная составляющие ускорения центра масс в момент старта.
Это реакция опоры /?, сила тяжести rn ^- g , сила тяги мышц FM и сила, нагружающая голеностопный сустав, F . Кроме того, на стопу действуют силы пассивного сопротивления, связанные с деформацией соединительных тканей и с силой трения в суставе.
|
|
|
Обозначим ускорение голеностопного сустава аст и воспользуемся связанной с ним неинерциальной системой отсчета. В этой системе сустав неподвижен, а стопа вращается вокруг него с некоторым угловым ускорением е. Согласно принципу Д'Аламбера к реальным силам следует добавить фиктивную силу инерции FK = —m - acj и записать условие вращения:
|
|
|
|
|
|
Глава 9
ЗАКОНЫ СОХРАНЕНИЯ
Консервативные силы,
Потенциальная энергия.
Закон сохранения энергии в механике
В механике есть силы, работа которых при перемещении тела по замкнутому контуру равняется нулю. Такие силы называются потенциальными, или консервативными.
Консервативной называется сила, работа которой при перемещении тела по замкнутому контуру равняется нулю.
Нетрудно показать, что консервативные силы обладают еще двумя свойствами:
1) работа консервативной силы при переходе тела из одного положения в другое не зависит от траектории движения, а определяется только начальным и конечным положениями тела;
2) при изменении направления перехода работа консервативной силы изменяет свой знак, не меняя величины Л, „ = —А2—г
Опираясь на закон всемирного тяготения и закон Гука, можно доказать, что сила тяготения и упругая сила являются потенциальными.
|
|
|
Потенциальность этих сил связана с тем, что на одном участке замкнутой траектории силы совершают положительную работу, а на другом — отрицательную так, что в сумме получается ноль. Покажем это на примере силы тяготения, действующей у поверхности Земли. Пусть тело проходит по замкнутой прямоугольной траектории 1—2—3—4—1 (рис. 9.1).

На участке 1—2 сила тяготения мешает движению, и ее работа отрицательна: At _2= —mgh . На участках 2—3 и 4—1 сила тяготения перпендикулярна направлению движения, и ее работа равна нулю: А2_3 = AA _ t = 0. На участке 3—4 сила тяготения помо гает движению, и ее работа положительна: А3_А = mgh . Полная работа на всем пути получается равной нулю:
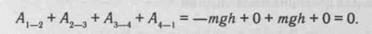
Не все силы являются потенциальными. Например, сила трения скольжения всегда направлена против движения тела и ее работа на всем пути — отрицательна. Сила трения не консервативна.
Работу консервативной силы удобно рассчитывать через уменьшение специальной величины — потенциальной энергии. Получим соответствующую формулу.
Пусть тело переходит из положения 1 в положение 2 (рис. 9.2). Выберем некоторую точку пространства (О) в качестве точки отсчета и рассмотрим траекторию движения, проходящую через эту точку: 1—О—2.
|
|
|
Потенциальной энергией тела (£п) называется скалярная величина, равная работе, совершаемой консервативной силой, при переходе тела из данного положения на выбранный уровень отсчета (О).

Таким образом, доказано, что работа консервативной силы равна убыли потенциальной энергии.
Дата добавления: 2019-01-14; просмотров: 363; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!



