Раздел 2. Дифференциальное исчисление функции одной переменной
В результате изучения раздела студент должен:
знать:
¾ определение производной, ее геометрический и механический смысл;
¾ правила и формулы дифференцирования функций; определение дифференциала функции и его геометрический смысл;
¾ определение второй производной;
¾ необходимые и достаточные условия возрастания и убывания функции, существования экстремума;
¾ необходимые и достаточные условия выпуклости и вогнутости графика функции;
¾ определение точки перегиба;
¾ общую схему построения графиков функций с помощью производной;
уметь:
¾ дифференцировать функции, используя таблицу производных и правила дифференцирования, находить производные сложных функций;
¾ вычислять значение производной функции в указанной точке;
¾ находить угловой коэффициент и угол наклона касательной, составлять уравнение касательной и нормали к графику функции в данной точке;
¾ находить скорость изменения функции в точке;
¾ применять производную для исследования реальных физических процессов (нахождения скорости неравномерного движения, угловой скорости, силы переменного тока, линейной плотности неоднородного стержня и т.д.);
¾ находить производные второго порядка, применять вторую производную для решения физических задач;
¾ находить дифференциал функции, с помощью дифференциала приближенно вычислять значение и приращение функции в указанной точке;
|
|
|
¾ применять производную для нахождения промежутков монотонности и экстремумов функции;
¾ находить с помощью производной промежутки выпуклости и вогнутости графика функции, точки перегиба;
¾ проводить исследования и строить графики функций.
Производная функции одной переменной. Правила дифференцирования. Производная сложной функции
Определение производной
Рассмотрим функцию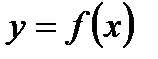 
, где 
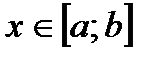(рис. 31). Возьмем произвольную точку 
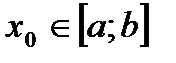. Для любого 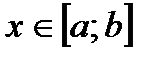разность х – х0 называется приращением аргумента х в точке х0 и обозначается 
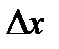. Таким образом,
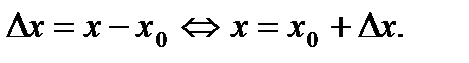
Разность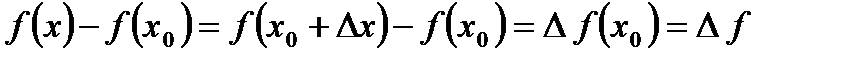 
называется приращением функции в точке х0.
Производной функции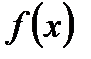 
в точке х0 называется предел отношения приращения функции 
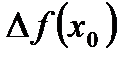к приращению аргумента 
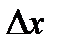при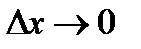 
, если этот предел существует и обозначается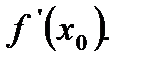 
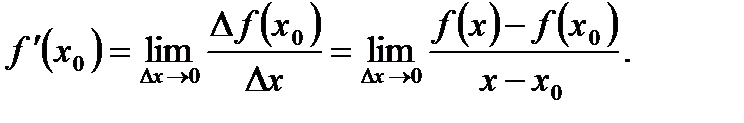
Пример. Вычислим по определению производную функции в заданной точке:
1) 
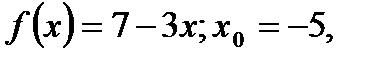
2)
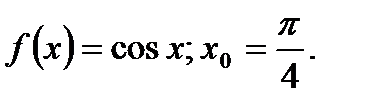
Решение. Согласно определению производной, имеем:
1) 
; 
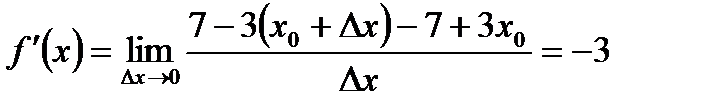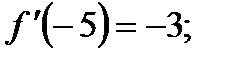
2) 
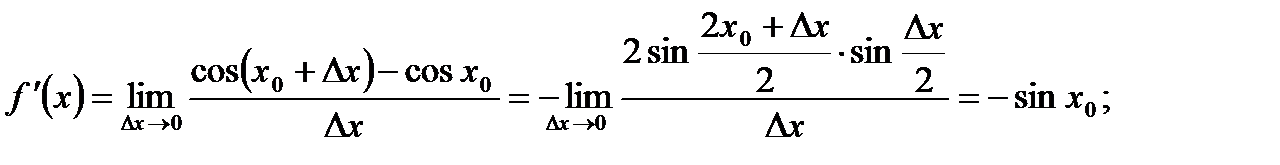
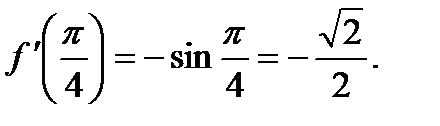
Ответ. 1) –3; 2) 4а + b; 3)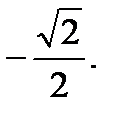 
Задание.Вычислить по определению производную функции в заданной точке: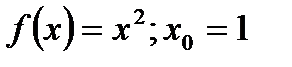 
Решение. __________________________________________________________________________________________________________________________________________________________Ответ: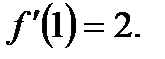 
|
|
|
Функция, имеющая производную в точке х0, называется дифференцируемой в этой точке. Если же функция дифференцируема в каждой точке некоторого интервала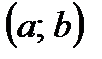 
, то она дифференцируема на этом интервале. Необходимое условие существования производной вытекает из следующей теоремы.
Теорема. Если функция 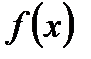дифференцируема в точке х0, то она непрерывна в этой точке.
Однако непрерывность функции в точке не является достаточным условием дифференцируемости функции в точке.
Пример. Функция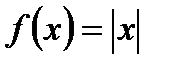 
непрерывна в точке х0 = 0, но не дифференцируема в ней, поскольку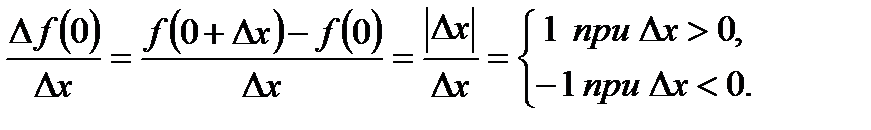 
Дата добавления: 2019-01-14; просмотров: 187; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!