Типовые звенья и их передаточные функциии
Практическое занятие №2
Тема: Операторный метод решения дифференциальных уравнений. Передаточная функция. Временные характеристики.
Цель: Получение практических навыков решения дифференциальных уравнений операторным методом, определения передаточных функций и временных характеристик элементов систем управления.
Исходные теоретические сведения
Операторный метод решения дифференциальных уравнений
Преобразование Лапласа. Множество функций 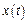 , удовлетворяющих условиям:
, удовлетворяющих условиям:
1. При 
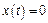 ;
;
2.  ;
;
3. Имеет место не более чем счетное число точек разрыва первого рода на
интервале [0,∞),
называется пространством оригиналов и обозначается О.
Введем комплексную переменную  и определим интеграл
и определим интеграл

 . (1)
. (1)
Функция  , определяемая зависимостью (1), где
, определяемая зависимостью (1), где  ,
,  , называется изображением
, называется изображением  и обозначается
и обозначается

или
 .
.
Часто интеграл (1) называют интегралом Лапласа. Его свойства определяются следующими теоремами:
1. Теорема линейности: если
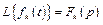
то
 .
.
2. Теорема смещения в комплексной области: если

то

3. Теорема смещения в действительной области: если
 ,
,
то
 .
.
4. Теорема изображения от производной:
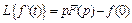 ,
,
…………………………

При 
 .
.
5. Теорема изображения от интеграла:

6. Теорема дифференцирования изображения:
 .
.
7. Теорема изменения масштаба во временной области: если
|
|
|
 ,
,
то

8. Теорема свертки функций в действительной области:

9. Теорема свертки в комплексной области:

Изображения по Лапласу наиболее часто используемых в теории управления функций приведены в табл. 1.
Таблица 1
Функции и соответствующие им изображения по Лапласу
| № | Наименование | Изображение 
| Оригинал 
|
| 1 | Дельта-функция | 1 | 
|
| 2 | 
| 
| |
| 3 | Ступенчатая единичная функция | 
| 
|
| 4 | Степенная функция | 
| 
|
| 5 | Экспонента убывающая | 
| 
|
| 6 | Экспонента возрастающая | 
| 
|
Продолжение табл.1
| 7 | 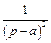
| 
| |
| 8 | 
| 
| |
| 9 | 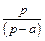
| ||
| 10 | 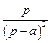
| 
| |
| 11 | 
| 
| |
| 12 | 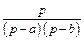
| 
| |
| 13 | 
| 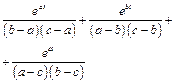
| |
| 14 | 
| 
| |
| 15 | 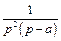
| 
| |
| 16 | 
 , ,
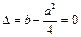

|



| |
| 17 | 
| 
|
Окончание табл. 1
| 18 | 
| 
| |
| 19 | 
| 
| |
| 20 | 
| 
| |
| 21 | 
| 
| |
| 22 | 
| 
|
Основы теории вычетов. Определение изображения любой функции по ее оригиналу обычно затруднений не вызывает. Однако решение обратной задачи чаще всего непросто: интегрирование сложного изображения  в общем случае может представить определенные трудности.
в общем случае может представить определенные трудности.
Однако есть виды уравнений, для которых эта задача решается сравнительно просто. Так, для линейных дифференциальных уравнений с постоянными коэффициентами она решается представлением  суммой простейших дробей, для которых существуют табличные значения оригиналов. Сложение этих оригиналов с учетом теоремы линейности дает представление оригинала
суммой простейших дробей, для которых существуют табличные значения оригиналов. Сложение этих оригиналов с учетом теоремы линейности дает представление оригинала  . Для получения такого разложения пользуются теорией вычетов, основные положения которой рассмотрены ниже.
. Для получения такого разложения пользуются теорией вычетов, основные положения которой рассмотрены ниже.
|
|
|
Согласно теореме обращения в любой точке t, где оригинал функции  непрерывен, функция может быть представлена в виде
непрерывен, функция может быть представлена в виде
 ,
,
где интегрирование ведется по любой бесконечной прямой  , лежащей в полуплоскости абсолютной сходимости интеграла Лапласа от
, лежащей в полуплоскости абсолютной сходимости интеграла Лапласа от  .
.
Если точка  является особой (правильной, изолированной) точкой функции
является особой (правильной, изолированной) точкой функции 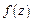 , то всегда можно найти простой контур C, однократно обходящий точку
, то всегда можно найти простой контур C, однократно обходящий точку  в положительном направлении, такой, что внутри этого контура
в положительном направлении, такой, что внутри этого контура  будет аналитической. Величина
будет аналитической. Величина

называется вычетом функции  относительно точки
относительно точки  . Если таких точек несколько, то вычет
. Если таких точек несколько, то вычет  по замкнутому контуру, охватывающему все эти точки, равен сумме вычетов
по замкнутому контуру, охватывающему все эти точки, равен сумме вычетов  относительно всех особых точек этой функции, находящихся внутри контура. Наконец, вычетом функции
относительно всех особых точек этой функции, находящихся внутри контура. Наконец, вычетом функции  относительно бесконечно удаленной точки естественно считать величину
относительно бесконечно удаленной точки естественно считать величину
|
|
|
 ,
,
где C – окружность бесконечного радиуса с центром в начале координат. Рассматриваются несколько частных случаев определения вычетов функций в зависимости от вида этих функций.
1. Если  – простой полюс функции
– простой полюс функции  , то в окрестности этой точки
, то в окрестности этой точки  представима в виде
представима в виде
 ,
,
где  непрерывна и аналитична в точке
непрерывна и аналитична в точке  , причем
, причем
 .
.
Отсюда, переходя к пределу, получим
 . (3)
. (3)
Пример 1. Вычислить вычет функции  относительно точки
относительно точки  .
.
Решение. Точка  является простым полюсом рассматриваемой функции, поэтому в соответствии с (3) получим
является простым полюсом рассматриваемой функции, поэтому в соответствии с (3) получим
 ,
,
а функция  представима в виде
представима в виде
 .
.
2. Если функция  является дробно-рациональной функцией, т.е. представлена в виде
является дробно-рациональной функцией, т.е. представлена в виде
 ,
,
при этом  и
и  - аналитические в точке
- аналитические в точке  и
и  – полюс первого порядка для
– полюс первого порядка для  , а
, а  , то по определению
, то по определению
 . (4)
. (4)
Пример 2. Вычислить
 .
.
Решение. Функция

имеет особые точки  , поскольку
, поскольку
 .
.
В соответствии с (4) получим
 .
.
3. Если точка  является полюсом порядка
является полюсом порядка  функции
функции  , то в окрестности этой точки
, то в окрестности этой точки
 .
.
Умножив обе части этого выражения на  и продифференцировав обе части
и продифференцировав обе части  раз, получим
раз, получим
|
|
|
 .
.
Точка  является нулем порядка не ниже
является нулем порядка не ниже  для функции
для функции  , т.е. в этой точке в нуль обращаются все ее производные до порядка
, т.е. в этой точке в нуль обращаются все ее производные до порядка  включительно. Следовательно, при
включительно. Следовательно, при  первое слагаемое выражения равно 0, и, переходя к пределу при
первое слагаемое выражения равно 0, и, переходя к пределу при  получим
получим
 . (5)
. (5)
Пример 3. Определить вычет функции  относительно точки
относительно точки  .
.
Решение. Указанная точка для рассматриваемой функции является полюсом третьего порядка, так как
 .
.
В соответствии с (5) получим


Используя теорему обращения, операторное отображение дифференциального уравнения можно представить суммой простейших дробей, знаменатели которых имеют вид  соответствующей кратности, а числители есть вычеты относительно корней
соответствующей кратности, а числители есть вычеты относительно корней  . Используя теорему линейности, решение дифференциального уравнения теперь можно описать суммой оригиналов полученных простейших дробей. Этот прием используется при решении дифференциальных уравнений операторным методом.
. Используя теорему линейности, решение дифференциального уравнения теперь можно описать суммой оригиналов полученных простейших дробей. Этот прием используется при решении дифференциальных уравнений операторным методом.
Операторный метод решения дифференциальных уравнений. Одним из важнейших применений операционного исчисления, связанных с преобразованием Лапласа, является решение дифференциальных уравнений с постоянными коэффициентами. Как мы уже знаем именно такими уравнениями описываются линейные системы управления. Поэтому операторный метод решения дифференциальных уравнений является одним из основных методов теории управления. Основные достоинства его состоят в следующем:
– он применим при любом виде правой части дифференциального уравнения, в том числе и при наличии в ней производных;
– получаемое решение не зависит от вида корней характеристического уравнения и их совпадения или несовпадения с коэффициентами правой части.
В основе операторного метода решения дифференциальных уравнений лежит переход из временной области в операторную область по теореме о дифференцировании оригиналов.
Пусть имеем дифференциальное уравнение
 . (6)
. (6)
Изображение переменных этого уравнения по Лапласу выглядит следующим образом:
– для левой части

и т.д.
– для правой части

и т.д. Тогда исходное дифференциальное уравнение может быть представлено в виде

откуда

Например, для неоднородного дифференциального уравнения второго порядка
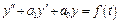 (7)
(7)
во временной области для получения выражения зависимости выхода от входа нет иного пути, кроме решения (интегрирования) этого уравнения. Преобразовав же его в комплексную плоскость с помощью преобразования Лапласа при начальных условиях
 ,
,  ,
,
получим
 . (8)
. (8)
В результате произведенной замены происходит переход от дифференциальной формы представления уравнения к алгебраической. Поскольку обе части уравнения отображены в одну и ту же область изображений, то проблем с выполнением аналитических преобразований больше нет, поэтому из (8) получаем
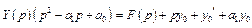 ,
,
откуда
 .
.
Далее остается вычислить оригинал полученной зависимости, воспользовавшись теоремой обращения, либо теорией вычетов, т.е. разложив полученное выражение на сумму простейших дробей и определив соответствующее табличное соответствие для каждой дроби.
Наиболее простой вид операторное решение (7) имеет при нулевых начальных условиях
 .
.
Отметим важное с этой точки зрения замечание: нулевые начальные условия соответствуют рассмотрению любого описываемого дифференциальным уравнением процесса, начиная с некоторого момента, принимаемого за начало отсчета, т.е. за нуль (оригинал  при
при 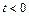 принимается равным нулю!). Именно такой подход используется при изучении процессов управления, так что использование дифференциальных уравнений с нулевыми начальными условиями для описания систем управления является вполне оправданным.
принимается равным нулю!). Именно такой подход используется при изучении процессов управления, так что использование дифференциальных уравнений с нулевыми начальными условиями для описания систем управления является вполне оправданным.
Передаточные функции
Определение передаточной функции. Пусть некоторая система управления описывается дифференциальным уравнением
 (9)
(9)
при нулевых начальных условиях. Используя свойства преобразования Лапласа перепишем (9) в изображениях

и определим отношение выходного сигнала системы к входному
 . (10)
. (10)
Это соотношение называется передаточной функцией. Она позволяет определить изображение выходного сигнала системы управления по изображению входного управляющего сигнала

Значения p, при которых передаточная функция обращается в нуль, называются нулями передаточной функции. Нули являются корнями полинома числителя, т.е. уравнения:

Значения, при которых передаточная функция обращается в бесконечность, называются полюсами передаточной функции. Полюсы являются корнями полинома знаменателя (характеристического полинома), т.е. уравнения:

Передаточная функция W(p) имеет, таким образом, m нулей и n полюсов. Как нули, так и полюса могут быть действительными или комплексно-сопряженными, поэтому их можно изобразить на комплексной плоскости (рис.1). Нули и полюса называются левыми (правыми), если они расположены в левой (правой) относительно мнимой оси части комплексной плоскости, и нейтральными или нулевыми, если они лежат соответственно на мнимой оси или в начале координат.
К показателям передаточной функции относятся:
– порядок передаточной функции n, равный степени знаменателя передаточной функции;
– степень rС, равная разности степеней знаменателя n и числителя m передаточной функции;

Рис. 1. Нули и полюса на комплексной плоскости.
*-полюса, ●-нули.
– индекс апериодической нейтральности sa, равный числу нулевых полюсов передаточной функции;
– индекс колебательной нейтральности sк, равный числу мнимых полюсов передаточной функции;
– индекс неустойчивости sH, равный числу правых полюсов передаточной функции;
– индекс неминимально-фазовости sнф, равный числу правых нулей передаточной функции.
Рассмотренные показатели содержат ценную информацию о свойствах исследуемой системы управления.
Ранее уже отмечалось, что если известны изображения входа Y(p) и передаточная функция W(p), то можно найти изображение выхода, а путем обратного преобразования – и сам выходной процесс. Таким образом, передаточная функция полностью характеризует динамические свойства системы (при нулевых начальных условиях).
Если W(p) есть дробно-рациональная функция, причем m < n и коэффициенты {a i} и {b i} действительные и известны корни многочлена A(p)=0, то выражение (10) можно переписать в виде:

где n i -кратность корня p i .
Известна формула
 ,
,
позволяющая представить оригинал передаточной функции суммой изображений вычетов передаточной функции относительно корней характеристического многочлена. Ниже представлены три различных варианта нахождения оригинала передаточной функции в зависимости от вида корней характеристического многочлена.
1. Пусть
 ,
,
где p1, p2, …, pn – различные вещественные и комплексные корни. Тогда оригинал находят по формуле

2. Если изображение имеет вид

то оригинал определяется выражением

3. Случай кратных корней. Пусть
 ,
,
где  , причем
, причем  . Тогда оригинал находят по формуле
. Тогда оригинал находят по формуле

Коэффициенты A jk определяются зависимостью

Нетрудно видеть, что описанные способы определения оригиналов передаточных функций в зависимости от вида корней характеристического уравнения полностью соответствуют способам определения вычетов в зависимости от вида дробно-рациональной функции.
Структурная схема алгоритма построения оригинала представлена на рис. 2.

Рис. 2. Структурная схема алгоритма построения оригинала:
Передаточные характеристики типовых звеньев. При изучении систем управления их схемы удобно представлять не в виде соединения ее элементов, классифицированных по функциональному назначению и принципу действия, а в виде структурной схемы, т.е. в виде соединения динамических звеньев. Динамическое звено – это математическая модель элемента или его части, записанная в виде дифференциального уравнения или передаточной функции.
В теории управления динамические звенья, которые описываются дифференциальными уравнениями не выше второго порядка, принято называть типовыми динамическими звеньями. Различают восемь типов звеньев, наименования и передаточные характеристики которых приведены в табл:2.
Таблица 2
Типовые звенья и их передаточные функциии
| Наименование звена | Передаточная функция |
| Усилительное (пропорциональное) | 
|
| Идеальное дифференцирующее | 
|
| Идеальное интегрирующее | 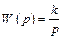
|
| Апериодическое первого порядка | 
|
| Форсирующее первого порядка | 
|
| Чистого запаздывания | 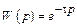
|
| Второго порядка: – консервативное – колебательное – апериодическое | 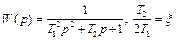



|
| Форсирующее второго порядка | 
|
Все динамические звенья обладают направленностью действия – от входа звена к его выходу, что на структурных схемах обозначается стрелками.
Временные характеристики
Динамические свойства элементарных звеньев могут описываться не только уравнениями и передаточными функциями, часто используют также временные и частотные характеристики. Эти характеристики могут быть получены экспериментально или построены по уравнению звена или по его передаточной функции. Возможно и обратное – по экспериментально построенным характеристикам можно составить уравнение звена или его передаточную функцию. Частотные характеристики будут рассмотрены в материалах к следующему практическому занятию. Здесь же мы рассмотрим временные характеристики – реакции системы на стандартные (типовые) входные воздействия, в качестве которых наиболее часто используются ступенчатое единичное воздействие (единичная функция) и δ-функция Дирака (единичный импульс). К числу этих характеристик относятся переходная и весовая функции.
Ступенчатое единичное воздействие (единичная функция) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным:
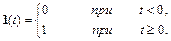
Операторное представление (изображение по Лапласу) ступенчатой единичной функции есть (см. табл. 1)
 .
.
d -функция Дирака (единичный импульс) – это импульс, площадь которого равна единице при длительности, равной нулю, и высоте, равной бесконечности:

Операторное представление (изображение по Лапласу) единичного импульса есть (см. табл. 1)
 .
.
Согласно определению d-функции справедливо:
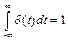
Связь d-функции с единичной функцией достаточно проста (следует, конечно, иметь в виду, что соотношение символическое, так как производная от d-функции, строго говоря, не существует):

Теперь найдем изображение выхода, если входом является d-функция.

Отсюда следует важный факт:передаточная функция равна изображению по Лапласу реакции системы на d-функцию. Оригинал изображения передаточной функции

называется импульсной переходной или весовой функцией системы. Она может иметь вид, в частности, представленный на рис. 3. Импульсная переходная функция, как и передаточная функция, является исчерпывающей характеристикой системы при нулевых начальных условиях.

Рис. 3
Теперь найдем изображение выхода, если входом является ступенчатая единичная функция.

Оригинал изображения отношения  , т.е.
, т.е.

называется переходной характеристикой (переходной функцией) системы.
Найдем связь между импульсной переходной функцией и переходной характеристикой. Поскольку
 ,
,
то

Так как при нулевых начальных условиях умножению изображения на p соответствует дифференцирование в области времени, то из последнего соотношения следует:
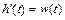
или
 .
.
Зная переходную или весовую функцию, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях:
 .
.
Временные характеристики типовых звеньев. Изображения передаточных функций типовых звеньев приведены в табл. 2. Описания временных характеристик этих звеньев приведены в табл.3 – 11.
Работа в аудитории
Анализ примеров
Пример 1.
Решить операторным методом дифференциальное уравнение
 ,
,
при
 .
.
Решение: С учетом начальных условий перейдем в операторную область:
– для левой части имеем:
 ;
;
– для правой части имеем:
 .
.
Воспользовавшись таблицами преобразования Лапласа, получаем:
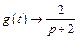 ,
,
тогда правую часть перепишем в виде:
 .
.
Следовательно, наше дифференциальное уравнение в операторной форме будет иметь вид:
 .
.
Приведем правую часть к общему знаменателю, имеем:

Выразим из полученного уравнения  :
:

Далее необходимо разложить дробь на сумму простых дробей, для этого найдем корни квадратного уравнения знаменателя:

Тогда изображение  можно представить в виде суммы простых дробей следующим образом:
можно представить в виде суммы простых дробей следующим образом:
 ,
,
где  – неизвестные коэффициенты.
– неизвестные коэффициенты.
Найдем коэффициент А, для этого умножим обе части равенства на  , и положим
, и положим  , имеем:
, имеем:
 ;
;
Найдем коэффициент В, для этого умножим обе части равенства на  , и положим
, и положим  , имеем:
, имеем:
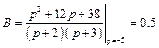 ;
;
Найдем коэффициент С, для этого умножим обе части равенства на  , и положим
, и положим  , имеем:
, имеем:
 .
.
С учетом найденных коэффициентов имеем:

Воспользовавшись таблицами преобразования Лапласа, получим:

Ответ: 
Пример 2. Дано операторное представление сигнала

Получить его оригинал.
Решение. Найдем корни характеристического уравнения:

Формула для оригинала, в соответствии с (2.8), имеет вид:

Имеем: A(0)=100; B(0)=12; B′(-3)= 1; B′(-4)=-1.
Тогда можно записать:
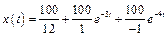 .
.
Пример 3. Найти решение уравнения

при  .
.
Решение. Операторное представление уравнения с учетом нулевых начальных условий имеет вид
 ,
,
откуда получаем:
 .
.
Для перехода к оригиналу используем общую формулу разложения. Поскольку в последнем выражении коэффициенты действительны, то вычеты в полюсах  представляют собой сопряженные комплексные числа. Поэтому достаточно вычислить только один вычет (второй отличается только знаком) в точке
представляют собой сопряженные комплексные числа. Поэтому достаточно вычислить только один вычет (второй отличается только знаком) в точке  .
.
 .
.
Удвоив действительную часть последнего выражения, получаем
 .
.
Ответ:  .
.
Пример 4. Найти решение уравнения
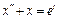
при ненулевых начальных условиях  ,
,  .
.
Решение. Положим  и
и  . Тогда уравнение и начальные условия перепишутся в виде
. Тогда уравнение и начальные условия перепишутся в виде
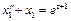 ,
,
где  ,
,  ,
,
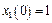 ,
,  .
.
Переходя к операторному представлению с учетом того, что

и
 ,
,
откуда
 .
.
Возвращаясь к оригиналам, получим
 .
.
Для получения окончательного решения произведем обратную замену  на
на  :
:
 .
.
Ответ: 
Дата добавления: 2019-01-14; просмотров: 924; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
