Метод Крамера. Методы Гаусса и главных элементов.

Стр 1 из 3Следующая ⇒

Лекция 3

2018/2019 уч. г.

Тема 4. Алгебра матриц

1. Алгебра матриц, основные определения. Определитель (детерминант) квадратной матрицы.

2. Равенство матриц. Сумма и разность матриц. Умножение матриц на число. Умножение матриц.

3. Транспонированная и обратная матрицы.

4. Ранг и нормы матрицы.

Литература.

1. Данилина Н.И. и др. Вычислительная математика: Учеб. пособие для техникумов. – М.: Высш. шк., 1985, с. 32-53, 78-83.

2. Демидович Б.П. Основы вычислительной математики: Учеб. пособие для высш. техн. учеб. заведений. М.: ФИЗМАТЛИТ, 1960, с. 225-245.

Контрольные вопросы и упражнения для приобретения

Умений и навыков по теме 4

1. Что называют матрицей размера m × n и ее элементом? Как сокращенно записывают матрицу? Приведите примеры диагональной и единичной матриц.

2. Какая матрица является квадратной? Что называют порядком квадратной матрицы?

3. Как определяется сумма и разность матриц A и B? Как вычисляется произведение двух матриц? В каком случае не может быть осуществлено умножение двух матриц? Даны две матрицы:

;

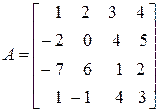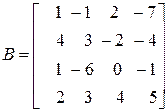
Вычислить A + B, A – B и A × B.

4. Записать для вышеприведенной матрицы A транспонированную матрицу D.

5. Что собой представляет определитель (детерминант) квадратной матрицы? Как вычисляется определители второго и третьего порядка? Вычислите определители следующих матриц

; .

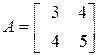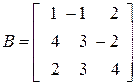6. Что называют минором M_il элемента a_ij определителя n –го порядка и что алгебраическим дополнением элемента a_ij определителя n –го порядка? Как вычисляется определитель матрицы через алгебраические дополнения? Вычислите определитель матрицы

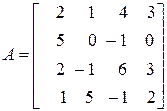7. Какая квадратная матрица называется обратной по отношению к заданной квадратной матрице? В каком случае квадратная матрица не имеет обратную ей матрицу?

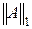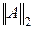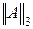8. Вычислите три нормы , и матрицы, приведенной в вопросе 6.

9. Что называют минором k –го порядка прямоугольной матрицы A

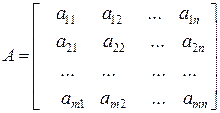
и что называют ее рангом? Как вычисляется ранг матрицы? Методом окаймления найдите ранг матрицы

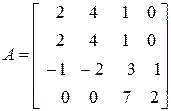Тема 5. Решение систем линейных уравнений

1. Постановка задачи нахождения корней системы линейных уравнений. Общая характеристика методов решения систем линейных уравнений.

2. Метод Крамера. Методы Гаусса и главных элементов.

3. Приближенные методы решения систем линейных уравнений. Метод итерации и метод Зейделя. Условия сходимости итерационного процесса.

4. Общие замечания о выборе метода решения систем линейных уравнений

1. Постановка задачи нахождения корней системы линейных

Уравнений. Общая характеристика методов решения систем

Линейных уравнений

Введение. Необходимость решения систем линейных алгебраических уравнений возникает при исследовании физических систем различной природы: механических, гидравлических, электрических и т.п. Например, рассмотрим следующую простую задачу.

Спроектировать кривошипно-шатунный механизм вида

удовлетворяющий следующим условиям:

i	φ_i	s_i
1	20^○	2,0
2	45^○	1,2
3	60^○	1,0

Исходя из геометрических построений, составим математическую модель, отражающую конструкцию кривошипно-шатунного механизма.

Из треугольников ABC и BDE находим

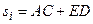; (1, в)

; ;

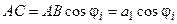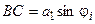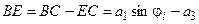. (2, в)

Из треугольника BDE имеем .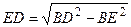

Учитывая (2, в), получим

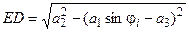Подставив ED и AC в уравнение (1, в), найдем

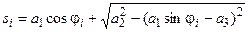После несложных преобразований получим

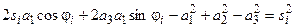Введем обозначения:

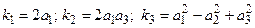. (3, в)

Тогда вышеприведенное уравнение примет вид:

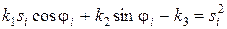Подставив в последнее уравнение условия, которым должны удовлетворять размеры звеньев механизма, получим его математическую модель в виде системы из трех линейных алгебраических уравнений

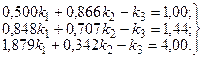
Решив эту систему относительно величин k₁, k₂, k₃ и далее, используя соотношения (3, в), найдем искомое решение поставленной задачи.

Постановка задачи решения системы. В общем случае систему m линейных уравнений с n неизвестными записывают в виде

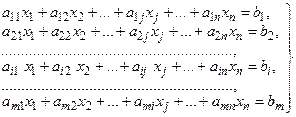(1)

или в краткой форме

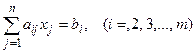в которой числа a_ij называются коэффициентами системы; b_i - свободными членами; x_i. - неизвестными.

Необходимо найти решение системы (1).

Заметим, что количество m уравнений в системе не обязательно совпадает с числом неизвестных: m может быть меньше, равно или больше числа n неизвестных.

Любая совокупность чисел α₁, α₂, …, α_n, которая при подстановке на место неизвестных x₁, x₁, …, x_n в уравнения системы (5) обращает все эти уравнения в тождества, называется решением системы (5) а сами числа α₁, α₂, …, α_n, корнями.

В общем случае, заданная система может либо не иметь решений, либо иметь единственное решение, либо иметь бесконечно много решений.

Рассмотрим следующие примеры систем линейных алгебраических уравнений.

Пример 1. Дана система

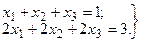
Эта система из двух уравнений с тремя неизвестными решений не имеет, так как любая тройка чисел, удовлетворяющая первому уравнению, не может удовлетворять второму.

Пример 2. Легко заметить, что система

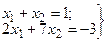
имеет единственное решение: .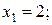

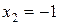Пример 3. Задана система уравнений

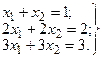
Данная система имеет бесконечно много решений. Например, пара чисел 0, 1 есть одно из решений этой системы; 2, -1 - другое решение, т.е. значения 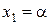и 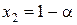при любом α удовлетворяют системе.

Приведенные примеры систем уравнений показывают, что система может либо не иметь решений, либо иметь единственное решение, либо иметь бесконечно много решений.

Система, не имеющая ни одного решения, называется несовместной. Система, обладающая хотя бы одним решением, называется совместной. Так, системы примеров 2 и 3 совместны, система примера 1 - несовместна.

Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, если они или обе несовместны, или обе совместны и имеют одни и те же решения.

В теории линейных уравнений показано, что любая система уравнений может быть переведена в эквивалентную ей систему с помощью элементарных преобразований. К ним относятся три типа преобразований:

1) перестановка двух уравнений системы;

2) умножение обеих частей уравнения системы на любое отличное от нуля число;

3) прибавление (вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Относительно каждой системы линейных уравнений обычно решаются следующие вопросы:

1. Совместна заданная система или нет?

2. В случае, если система совместна, как определить, сколько она имеет решений - одно или несколько?

3. Как найти все решения системы?

В дальнейшем, при ответах на эти вопросы ограничимся рассмотрением систем, у которых число уравнений равно числу неизвестных.

Пусть дана система n линейных уравнений с n неизвестными:

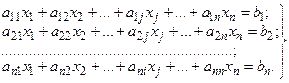(2)

Введем понятие матрицы системы. Матрицей системы (2) называется матрица, составленная из коэффициентов при неизвестных этой системы:

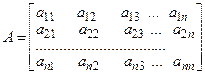С матрицей связан определитель (детерминант)

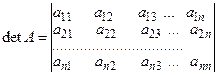который представляет собой число, определяемое по определенным правилам [2]. Приведем без доказательства следующую теорему.

Теорема Крамера. Система из n линейных уравнений с n неизвестными, определитель которой отличен от нуля, всегда совместна и имеет единственное решение.

Положение этой теоремы хорошо иллюстрируется геометрически применительно к системе из двух уравнений

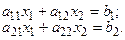
Каждому из этих уравнений соответствует прямая в плоскости x₁, x₂ (рисунок 2). При detA ≠ 0 эти прямые пересекаются и координаты точки их пересечения есть решение системы.

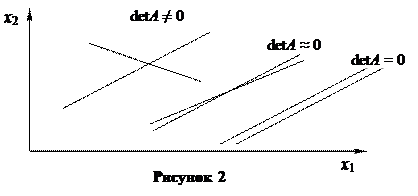Замечание 1. Если определитель системы (2) равен нулю (detA = 0), то возможны два случая:

- прямые уравнений параллельны между собой, что указывает на несовместность системы (система не имеет решений);

- прямые уравнений совпадают и, следовательно, система имеет бесконечно много решений.

Замечание 2. Значение определителя системы (2) не равно нулю, но близко к нему (detA ≈ 0). В этом случае прямые уравнений пересекаются между собой под очень малым углом и небольшое изменение наклона или сдвиг прямой одного из уравнений сильно изменяет положение точки пересечения прямых этих уравнений, т.е. имеет место большое изменение решения системы.

Это свидетельствует о возникновении вопроса об устойчивости решения системы уравнений относительно погрешностей значений коэффициентов a_ij и свободных членов b_i этих уравнений. Если небольшое изменение значений коэффициентов a_ij или свободных членов b_i уравнений приводит к существенным изменениям результатов решения системы, то такую систему называют плохо обусловленной и осуществляют отдельные исследования вопроса об устойчивости решения системы уравнений.

Общая характеристика методов решения систем линейных уравнений. Способы решения систем линейных уравнений разделяются на две группы: прямые (точные) и итерационные (приближенные). Прямыми являются методы, которые в предположении, что вычисления ведутся без округлений, позволяют получить точное решение за конечное число арифметических операций. К таким методам относятся, например, метод Крамера, метод Гаусса, метод главных элементов, метод квадратных корней и др.

Вместе с тем, поскольку на практике все вычисления ведутся с округлениями, то и значения искомых неизвестных, полученными точными методами, неизбежно будут содержать погрешности вычислений, причем оценка погрешности найденного решения системы в общем случае затруднительна. Кроме того, реализация точных методов с применением ЭВМ обусловлена возможностями современной вычислительной техники. В частности, при решении системы из n уравнений методом Крамера для непосредственного вычисления определителей этой системы с n неизвестными потребуется порядка n!n арифметических операций (например, 100!= 10^157,9…).

Итерационные методы даже в предположении, что вычисления ведутся без округлений, дают приближенное решение системы с наперед заданной точностью. Точное решение этими методами теоретически может быть получено как результат бесконечного процесса. К приближенным методам относятся метод итерации, метод Зейделя, метод релаксации и др.

Метод Крамера. Методы Гаусса и главных элементов.

Метод Крамера. Пусть дана система n линейных уравнений с n неизвестными:

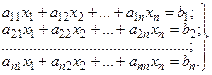. (3)

Найти решение этой системы.

Если для матрицы A

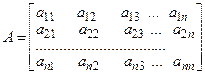
ее определитель

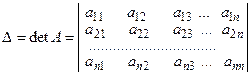
отличен от нуля, то решение системы (3) может быть найдено по формулам

; ;…; ,

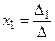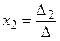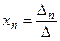где 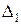, , 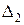…, 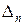- определители, полученные из определителя 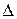путем замены его j -го столбца столбцом свободных членов системы (3), например, определитель 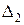для вычисления корня x₂ системы имеет вид:

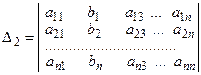
Пример. Дана система из 4-х линейных уравнений

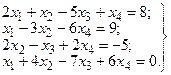
Найти решение этой системы.

Решение.

Вычислим определитель заданной системы уравнений. Находим

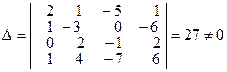Вычислим определители 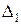, , 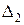, , 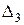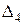полученные из определителя 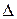заменой его j -го столбца столбцом свободных членов системы:

; ;

; .

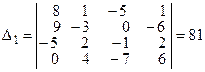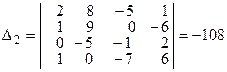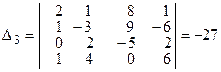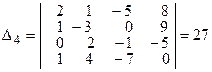Следовательно, решение заданной системы уравнений равно:

; ; ; .

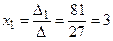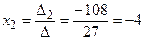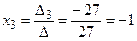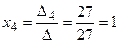Решение системы линейных уравнений методом Гаусса. Метод Гаусса является одним из наиболее распространенных методов решения систем линейных уравнений. В основе его лежит идея последовательного исключения неизвестных, позволяющая построить новую, эквивалентную исходной, систему уравнений с треугольной матрицей. В такой системе последнее уравнение содержит только одну неизвестную, а в каждом последующем уравнении добавляется ещё по одной неизвестной.

Рассмотрим методику метода Гаусса.

Пусть необходимо решить систему уравнений c n неизвестными:

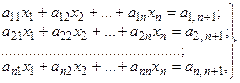(4)

в которой a_i_,_n₊₁ = b_i, например

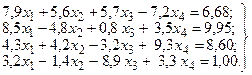. (5)

Назовем коэффициент a₁₁ ведущим элементом первой строки. Для него должно соблюдаться условие a₁₁ ≠ 0, в противном случае необходимо переставить уравнения системы (5) так, чтобы это условие соблюдалось.

Разделим первое уравнение на ведущий элемент a₁₁. Получим новое уравнение:

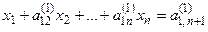(6)

Для числового примера имеем a₁₁ = 7,9. Следовательно:

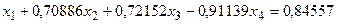. (7)

Используя полученное уравнение, легко исключить из остальных уравнений системы (4) начиная со второго, неизвестную x₁. Для этого достаточно из второго уравнения системы (4) вычесть уравнение (6) умноженное на a₂₁ затем из третьего уравнения системы (4) вычесть уравнение (6), умноженное на a₃₁ и т. д. В результате получим:

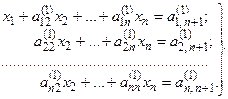(8)

Заметим, что вычисление коэффициентов системы (8) выполнялось по формулам:

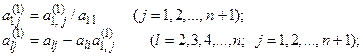
Выполняя эти действия для числового примера, получим следующую систему:

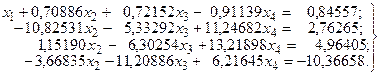(9)

Поступая аналогичным образом, исключим неизвестную x₂ в системе (8). Разделим второе уравнение системы (8) на ведущий элемент a₂₂. Последовательно умножая полученное уравнение на a₃₂, a₄₂,…, a_n₂ и вычитая из третьего, четвертого,…, n – го уравнений системы (8), получим

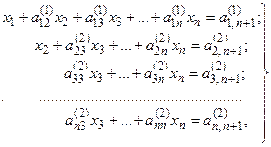(10)

где коэффициенты 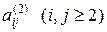вычислялись по формулам

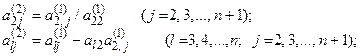
Для числового примера имеем

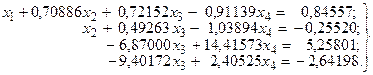(11)

Перечисленные действия повторяются до тех пор, пока не будут исключены неизвестные x₃, x₄,…, x_n_-1. В результате исходная система (4) будет приведена к эквивалентной системе с треугольной матрицей:

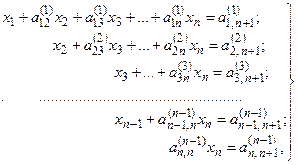(12)

в которой коэффициенты вычислялись по формулам

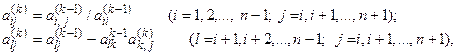
где k - номер шага преобразования исходной матрицы, состоящего из всех действий по исключению одной из неизвестных, начиная с деления на ведущий элемент (k = 1, 2, 3, …, n-1).

Для числового примера исключение неизвестной из четвертого уравнения системы (11) представляет собой последний шаг преобразования исходной системы (5) к системе с треугольной матрицей:

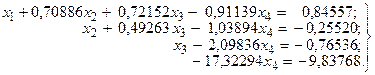(13)

Из последнего уравнения полученной системы (12) находим

Остальные неизвестные, начиная с x_n_-1, последовательно определяем из n-1, n-2, …, первого уравнения по формуле

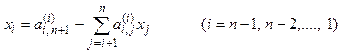Так, для системы (13) получим следующее решение:

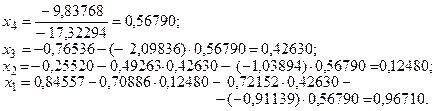
Таким образом, процесс решения линейной системы уравнений (4) методом Гаусса сводится к построению эквивалентной системы (12), имеющей треугольную матрицу. Необходимым и достаточным условием применимости метода является неравенство нулю всех ведущих элементов. Процесс приведения исходной системы к системе треугольного вида называется прямым ходом, а процесс вычисления значений неизвестных - обратным ходом, так как сначала определяется значение последнего неизвестного.

Обычно вычисления по методу Гаусса ведут с составлением таблицы, в которую записывают результаты вычислений коэффициентов и свободных членов системы уравнений в ходе её преобразования [2]. При этом дополнительно вычисляют так называемые «контрольные суммы» равные сумме коэффициентов отдельных уравнений и их свободных членов: 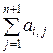. Столбец таких сумм помещают рядом со столбцом свободных членов и проделывают с такие же действия, как и со свободными членами. Признаком правильности выполненных действий на каждом шаге преобразования системы является то обстоятельство, что в каждом вновь полученном уравнении сумма его коэффициентов и свободного члена должна совпадать с вновь полученным значением "контрольной суммы" (в пределах ошибок округления). Большие отклонения от "контрольной суммы" свидетельствуют о наличии грубой ошибки в вычислениях.

Метод Гаусса позволяет построить достаточно простой алгоритм по вычислению корней системы линейных уравнений (рисунок 3).

Исходными данными являются порядок системы и двухмерный массив действительных переменных - коэффициентов и свободных членов системы уравнений. Этот массив состоит из n строк и n+1 столбцов, причем свободные члены b_i размещаются в конце каждой i-й строки, т.е. обозначаются так же, как в системе (8), через переменные a_i_,_n₊₁. В приведенной на рисунке 3 схеме алгоритма блоки 4-10 описывают процесс приведения исходной системы уравнений к эквивалентной, но треугольного вида. При этом промежуточные и окончательные значения элементов преобразуемой системы располагаются в том же массиве. Значения диагональных элементов матрицы коэффициентов (ведущих элементов) перед началом преобразования строк присваиваются промежуточной переменной d (блок 5) c тем, чтобы сохранить эти значения до окончания преобразования очередной строки матрицы. Алгоритм построен для случая, когда d ≠ 0 на любом шаге преобразования.

Блоки 11-17 описывают процесс обратного хода метода Гаусса, т.е. последовательного вычисления неизвестных x_i начиная с x_n (блок 11).

О некоторых ограничениях, которые могут возникнуть при применении приведенного алгоритма.

1. Преобразование матрицы исходной системы уравнений к треугольному виду нельзя проводить, если в ходе преобразований на главной диагонали оказался нулевой элемент 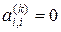(например, на k -м шаге преобразования). В этом случае перестановкой строк перемещают на главную диагональ ненулевой элемент и продолжают вычисления.

2. Возможна ситуация, когда на главной диагонали окажется очень малый по величине элемент. При делении на него будут получены большие числа с большими абсолютными погрешностями. В результате этого решение системы сильно исказится.

Чтобы избежать катастрофического влияния вычислительной погрешности, применяют метод Гаусса с выбором главного элемента. В отличие от рассмотренной схемы с выбором ведущего элемент в данном случае на каждом k -м шаге преобразования находят в k -м столбце главный элемент, т. е. наибольший по модулю, и перестановкой строк переводят его на главную диагональ. После этого производят дальнейшее преобразование матрицы. Это несколько усложняет алгоритм решения, но во многих случаях позволяет уменьшить погрешность округления при вычислениях.

Дата добавления: 2019-01-14; просмотров: 588; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!