Моделирование на ЗВМ вибраций

Стрелки вибрографа

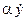Содержательная постановка задачи. Для регистрации колебательных процессов при наличии случайных возмущений (толчки, удары) применяются низкочастотные вибрографы, имеющие для гашения возникающих колебаний демпферы вязкого трения. Принципиальная схема такого прибора приведена на рис. 1. Здесь движение массы m, подвешенной на пружине жесткостью с, демпфируется силой вязкого трения,  где 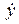 – скорость смещения массы относительно основания, α – коэффициент вязкого сопротивления демпфера прибора. Однако в момент снятия показаний прибора наблюдается вибрация стрелки прибора, обусловленная вибрацией основания прибора.

Определить, как изменяется смещение стрелки прибора относительно шкалы, закрепленной на основании прибора во времени, если основание движется по закону

 

,

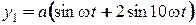в котором

y₁ – перемещение основания прибора;

a – амплитуда колебаний основания вибрографа;

ω – частота колебаний основания;

t – время.

 

Математическая модель колебательного движения массы m прибора. Используя математический аппарат физики и теоретической механики, можно установить, что колебание массы прибора относительно станины описывается дифференциальным уравнением

 

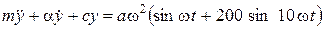,                    (1)

с начальными условиями:

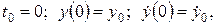                                (2)

 

где: y - смещение массы относительно основания; m – масса чувствительного элемента вибрографа; α – коэффициент вязкого сопротивления демпфера прибора; c – жесткость пружины.

Таким образом, задача о вибрациях стрелки прибора представляет собой математическую задачу Коши решения дифференциального уравнения (1) с начальными условиями (2).

 

Задание

 

1. Исследовать на ЭВМ величину отклонения стрелки вибрографа в зависимости от частоты колебаний основания w, изменяющейся от 10 до 400 с .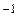

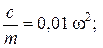
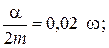
Исходные данные:  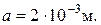Интервал времени исследования процесса .

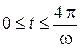2. При разработке алгоритма и программы моделирования колебательного процесса использовать метод Рунге-Кутта IV порядка для вычисления значений величины перемещения стрелки прибора. Для тестирования программы решения дифференциального уравнения достаточно иметь контрольные значения перемещения стрелки прибора в двух-трёх точках начального участка интервала интегрирования уравнения.

 

Литература

 

2. Моделирование технических объектов на макроуровне: Метод. указания. /А.С. Донсков: Перм. гос. техн. ун-т. Пермь, 2007. – 24 с.

Тема № 13

Задача расчета торцового размера по шарикам для контроля точности

изготовления косозубого цилиндрического колеса

 

 

Существенное повышение качества выпускаемых изделий машиностроения достигается наряду с совершенствованием методов механической обработки деталей и металлообрабатывающего инструмента, совершенствованием способов и средств контроля показателей качества деталей. Нередко при разработке методик контроля точности размеров изготовленных деталей возникают задачи, решение которых требует применение методов вычислительной математики. В частности, такие задачи имеют место при определении номинальных значений торцового размера по шарикам (роликам) для контроля точности изготовления зубчатых колес внешнего (внутреннего) зацепления с четным (нечетным) числом зубьев. Одна из таких задач предложена для решения в данной теме курсовой работы.

 

Постановка задачи. Разрабатывается технологический процесс изготовления косозубого цилиндрического колеса внутреннего зацепления с нечетным числом зубьев. В технологическом процессе, наряду с операциями механической обработки, предусматривается контроль точности изготовления зубчатых колес. Определен контролируемый показатель точности обработки - торцовый размер M по шарикам, вложенным в противоположные впадины зубчатого колеса (рис. 1).

Полученное при измерении значение размера сравнивают с номинальным значением М, которое предварительно рассчитывают, используя математическую модель схемы измерения контролируемого показателя точности обработки.

Вычислить размер М для контроля точности изготовления косозубого цилиндрического колеса с внутренним зацеплением, имеющего нечетное число зубьев.

 

Математическая модель. Математическая модель контролируемого торцового размера M построена, исходя из геометрической модели этого параметра (рис. 1) и основных понятий теории механизмов и машин.

Так из геометрических построений, приведенных на рис. 1 имеем

 

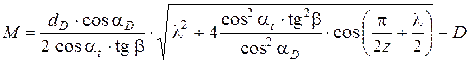.        (1)

 

 

В этой формуле величины α_t, d_D, d составляют:

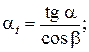
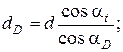
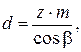                       (2)

 

а величины α_D и λ находятся и решения уравнений:

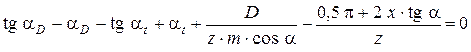;  (3)

 

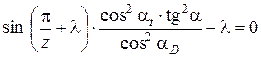;                        (4)

 

В этих зависимостях: m – модуль зубчатого колеса, мм; z – число зубьев колеса; α – угол главного профиля, рад.; β – угол наклона зуба, рад.; x – коэффициент смещения исходного производящего контура инструмента относительно обрабатываемого зубчатого колеса; D – диаметр шарика, мм.; α_t – угол профиля, рад.; α_D – угол профиля зуба на окружности, проходящей через центры шариков, рад.; d_D – диаметр окружности, проходящей через центры шариков, мм.; d – диаметр делительной окружности, мм.; λ – параметр профиля зуба, рад.;

 

Полученные уравнения (3), (4) являются трансцендентными и определение параметров профиля зуба α_D и λ представляет собой чисто математическую задачу решения этих уравнений.

 

Задание

1. Выбрать численный метод решения уравнений (3), (4). Привести обоснование выбора метода.

2. Выполнить постановку вычислительной задачи. Разработать алгоритм реализации численного метода на ЭВМ.

3. Составить тесты отладки программы для расчета параметров α_D и λ, приняв в качестве исходных данных следующие значения входных параметров:

m = 6 мм; z = 29; α = 20°; β = 16°; x = - 0,3; D = 10,319 мм.

4. Вычислить торцовый размер M по шарикам зубчатого колеса.

 

Замечание. Исходным интервалом для отделения корней уравнений (3), (4) является отрезок [0; π/2]. Погрешность найденных значений корней α_D и λ не должна превышать 10^-4 рад.

 

 

Тема № 14

 

Задача аппроксимации интерполяционным многочленом Лагранжа

функции геометрии области контакта сжатых двух упругих тел

 

При определении механических свойств материалов, проектировании различных технических устройств и разработке способов механической обработки деталей, в частности, методами поверхностного пластического деформирования, возникает необходимость решения задачи о контакте двух тел (так называемая контактная задача). В самом общем случае контактная задача формулируется в следующем виде.

Пусть имеются два тела, ограниченные нелинейными поверхностями, первоначально соприкасающиеся в точке. К ним приложена сила сжатия, действующая в направлении нормали к граничным поверхностям тел, проходящей через точку их касания.

Какие напряжения и деформации возникают в сжатых телах в точках окрестности их контакта.

Результаты решения контактной задачи имеют практическую ценность для определения несущей способности деталей машин и механизмов, выбора режима обработки деталей методами пластического деформирования, выявления механизма формирования качества поверхностного слоя деталей и т. п.

В настоящее время всесторонне изучена контактная задача для случая упругого сжатия тел и с помощью математического аппарата теории упругости получены математические модели, отражающие различные стороны взаимодействия двух тел при их сжатии. В частности, построена математическая модель геометрических параметров области контакта при сжатии двух упругих тел, которая имеет следующий вид.

Математическая модель контакта двух упругих тел. При сжатии двух тел, ограниченных нелинейными поверхностями с радиусами кривизны 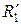,  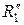и 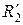,  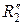в главных нормальных сечениях, они будут взаимодействовать не в одной точке их первоначального касания, а по некоторому малому участку их поверхностей. Этот участок их взаимодействия называется площадкой контакта, а ограничивающая ее кривая – контуром площадки контакта. Установлено [1], что при упругом сжатии тел, поверхность их контакта представляет собой эллиптическую площадку с эксцентриситетом е, который находится из решения уравнения:

 

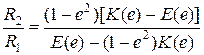,                                      (1)

 

в котором K(е)и Е(е) – эллиптические интегралы первого и второго рода

 

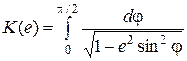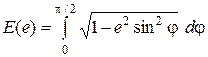, ;           (2)

1/R₁, 1/R₂ – приведенные кривизны поверхностей тел в точке их касания .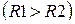

По найденному значению эксцентриситета эллиптической площадки контакта в дальнейшем вычисляются ее большая a и малая b полуоси по формулам:

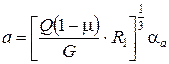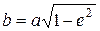, ,                              (3)

где 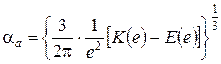; Q – сила сжатия тел;  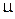– коэффициент Пуассона материала деформируемого тела; G – модуль сдвига материала; R₁ – наибольший из радиусов приведенных кривизн 1/R₁, 1/R₂ поверхностей тел в точке их первоначального касания.

Приведенные кривизны 1/R₁, 1/R₂ поверхностей тел в точке их первоначального касания зависят от геометрической формы соприкасающихся поверхностей и взаимного расположения их главных нормальных сечений. В технических устройствах наиболее часто имеет место контакт тел, ограниченных поверхностями вращения. При этом оси этих поверхностей могут располагаться параллельно или накрест друг другу, а сами поверхности находиться при внешнем или внутреннем соприкасании.

В работе [1] приведены формулы для величин 1/R₁, 1/R₂ в зависимости от конкретных условий соприкасания тел, вычисление значений R₁ и R₂ по которым не вызывает каких-либо затруднений. Однако определение геометрических параметров области контакта сопряжено со значительными затруднениями, обусловленными нахождением решения уравнения (1) и вычислением значений интегралов (2), подынтегральные функции которых не имеют первообразных. При этом приходится одновременно решать две взаимосвязанные задачи вычислительной математики – задачу нахождения корня нелинейного уравнения (1) и численного решения интегралов (2).

В отдельных случаях можно избежать необходимость решения вышеуказанных математических задач, используя таблицу [1], в которой для отдельных значений отношения R₂/R₁ приведены соответствующие значения эксцентриситета e и значение коэффициента α_a формулы (3) для полуоси a площадки контакта. Однако при решении практических задач далеко не всегда в таблице имеется информация о значениях e и α_a для полученного в задаче отношения R₂/R₁. Кроме того, возможна ситуация отсутствия самой таблицы. Вместе с тем проблема поиска величин e и α_a значительно упрощается при наличии интерполяционных многочленов, аппроксимирующих аналитическую зависимость e и α_a от величины отношения R₂/R₁.

 

 

Задание

 

1. В приведенной ниже таблице приведены значения отношения R₂/R₁ и коэффициента α_a для наиболее часто используемых в технических задачах значений эксцентриситета e². Построить интерполяционные многочлены Лагранжа, описывающие зависимости величин R₂/R₁ и α_a от эксцентриситета e².

2. Выполнить постановку вычислительной задачи. Разработать алгоритм реализации численного метода на ЭВМ.

3. Вычислить коэффициенты выбранного вида многочленов для функций R₂/R₁ и α_a и произвести проверку работоспособности полученных многочленов.

4. Произвести оценку погрешностей полученных многочленов.

 

Таблица

 

R2/R1	1	0,925	0,846	0,765	0,682	0,594	0,502	0,405	0,297
αa	0,722	0,731	0,741	0,753	0,767	0,783	0,803	0,829	0,863
e2	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8

 

Литература

 

1. Лурье А.И. Теория упругости. М.: Наука, 1970. – 940с.

 

 

---

Дата добавления: 2019-01-14; просмотров: 195; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!