Составление программы и ее отладка
Это завершающий этап подготовки задачи для ее решения на ЭВМ. Программа решения даже простой задачи может иметь ошибки (это естественное явление!), они могут являться синтаксическими или семантическими (логическими). Поэтому подготовка задачи для ее решения на ЭВМ всегда завершается отладкой программы, т. е. поиском и устранением ошибок. Успешную отладку программы можно осуществить только ее тестированием, для чего предварительно должен быть подготовлен тест с контрольным результатом решения задачи, полученным “вручную”.
Последовательность выполнения курсовой работы
В нижеследующей таблице представлен график выполнения курсовой работы.
Таблица. График выполнения курсовой работы
| № пп | Неделя семестра | Этап работы | Формы контроля |
| 1 | 8 | Получение и осмысление задания | Собеседование |
| 2 | 9-10 | Изучение теоретического и практического материала о методах решения математической модели объекта | Просмотр теоретической части работы |
| 3 | 11-12 | Выбор и обоснование численного метода. Постановка вычислительной задачи | Аттестация результатов выполнения |
| 4 | 13 | Построение схемы алгоритма решения задачи. Подготовка теста | Консультация |
| 5 | 14-15 | Оформление пояснительной записки | |
| 6 | 16-17 | Защита курсовой работы | Собеседование |
Выполнение курсовой работы начинается с глубокого осмысления полученного задания. Следует выяснить уровень и детализацию приведенной в задании задачи (на содержательном уровне, на уровне математической модели и т.п.), какой объект подвергается исследованию, какие цели должны быть достигнуты, какие данные будут обрабатываться на ЭВМ и т.д. Необходимо ознакомиться с основными сведениями по затрагиваемым в задании вопросам в рекомендуемой литературе. Учитывая, что основными задачами курсовой работы являются выбор численного метода решения математической модели объекта и разработка алгоритма его реализации на ЭВМ, следует достаточно глубоко изучить теоретический и практический материал о методах решения класса задач, к которому относится приведенная в теме задания математическая модель объекта исследования. При этом перечень приведенной в задании литературы может быть расширен.
Качественно выполненный анализ задания позволит определиться, прежде всего, с основными этапами выполнения задания, а также в значительной степени уменьшит непроизводительные затраты времени и сил при выполнении курсовой работы.
Результаты анализа задания должны быть обсуждены с руководителем курсовой работы. Только после собеседования по вопросам темы задания приступают к выполнению курсовой работы в соответствии с нижеприведенным графиком. Выполнение графика работы во времени является обязательным. Естественно, что приведенные временные рамки осуществления тех или других этапов могут быть сокращены исполнителем работы. Досрочное выполнение курсовой работы поощряется при ее защите.
Оформление результатов курсовой работы
Результаты выполненной курсовой работы оформляются в виде пояснительной записки. По своей структуре пояснительная записка должна иметь следующие разделы:
1) титульный лист;
2) содержание с указанием страниц;
3) тема задания;
4) краткие сведения о поставленной проблеме;
5) математическая модель исследуемого объекта;
6) теоретические сведения о методах решения математической модели;
7) постановка вычислительной задачи, исходные данные;
8) алгоритм решения задачи, разработка теста;
9) список литературы;
10) приложения (таблицы, графики результатов тестирования).
Отметим основные моменты содержания отдельных разделов пояснительной записки
Оформление титульного листа осуществляется в соответствии с формой, приведенной в приложении.
В кратких сведениях о поставленной проблеме необходимо привести, какой объект (явление, процесс, устройство) рассматривается в задании, какой моделью описывается объект исследования (статической, динамической), как она получена (на основе какие данных, какие литературные источники были использованы и т.п.).
Математическая модель объекта задачи, как правило, относится к определенному классу математических задач. В связи с этим в пояснительной записке следует дать общую характеристику этого класса задач (область техники, где возникает необходимость решения таких задач, их математическую формулировку в общем виде) и численных методов их решения. При описании методов решения указать, что составляет общую основу этих методов (идеи, подходы, предпосылки), какой математический аппарат используется при их реализации.
Достаточно подробно должен быть изложен выбранный метод решения, дано обоснование его использования для приведенной в задании модели с точки зрения точности искомых результатов, времени решения, ресурсов памяти ЭВМ и т.п.
В постановке вычислительной задачи следует отметить вид задачи (прямая, обратная, идентификации) с приведением формул, уравнений, по которым должно быть найдено решение задачи. Здесь же приводятся основные сведения о входных данных (структура, диапазон изменения и т.п.) и искомых величинах.
В разделе «Алгоритм решения задачи» следует указать, решение каких отдельных подзадач составляет общий процесс исследования объекта, дать описание укрупненной схемы алгоритма, описания схем алгоритмов решения отдельных подзадач.
При описании теста отладки программы необходимо указать для каких значений входных данных получены контрольные результаты решения отдельных подзадач и задачи в целом, дать обоснование этого выбора данных.
В записке должна быть приведена вся последовательность расчета теста: исходные формулы в общем виде, формулы с подставленными в них конкретными числовыми значениями, результаты вычислений, в том числе и промежуточных. Если при подготовке теста использовались таблицы или известные результаты решения отдельных подзадач, то приводятся литературные источники этих данных.
Защита курсовой работы
К защите курсовой работы предъявляется пояснительная записка. Защита осуществляется в форме собеседования по теме задания. При этом исполнитель работы должен показать свои умения и навыки использования знаний методов вычислительной математики при решении математических моделей объектов машиностроения.
Ниже приведены темы курсовых работ.
Тема №1
Задача расчета параметров схемы затылования металлорежущего
инструмента по дуге эксцентрической окружности
Постановка задачи. Для получения режущего клина на зубе инструмента осуществляют его заточку с образованием заднего угла α (рис. 1). Это угол между касательной mо к окружности, проходящей через вершину зуба и имеющей центр на оси вращения инструмента, и касательной mз к задней поверхности в той же точке инструмента (вершине зуба).
 |
Существует несколько способов образования заднего угла. Самым простым способом является заточка инструмента по прямой линии (рис. 1, а). Этот способ позволяет произвести заточку инструмента по задней поверхности без использования каких-либо специальных приспособлений. Однако образованный таким способом режущий клин не восстанавливается при перезаточке инструмента по мере износа. Кроме того, при заточке по прямой линии происходит ослабление вершины зуба. Поэтому у тяжелонагруженного фасонного инструмента заднюю поверхность зуба выполняют по дугам сложных кривых (затылуют) – по спирали Архимеда, дуге эксцентрической окружности, дуге гипотрохоиды (рис. 1, б, в, г). Это предоставляет возможность при образовании на задней поверхности зуба инструмента площадки износа с нулевым задним углом переточить инструмент с образованием плоскости на передней поверхности зуба. При этом практически восстанавливается исходный задний угол.
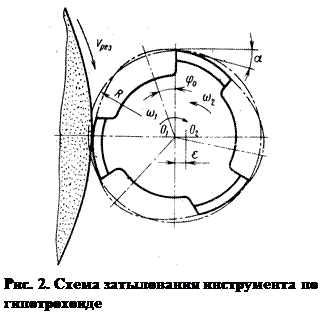
Затылование по дугам кривых требует строгой ориентации в пространстве перезатачиваемого инструмента относительно заточного (шлифовального круга), а также согласования движений обрабатываемого и обрабатывающего инструментов во времени и пространстве. При затыловании по дуге окружности, центр которой не проходит через центр инструмента (рис. 2), ориентация в пространстве перезатачиваемого инструмента относительно заточного круга определяется двумя параметрами:
-  углом затылования φ – углом поворота относительно оси абсцисс радиуса Rи, на котором лежит центр затылуемой окружности;
углом затылования φ – углом поворота относительно оси абсцисс радиуса Rи, на котором лежит центр затылуемой окружности;
- эксцентриситетом ε, на который смещена окружность затылования относительно центра инструмента.
Таким образом, для выполнения операции затылования зуба инструмента по дуге окружности, прежде всего, определяют параметры установки затачиваемого инструмента относительно заточного круга, решая следующую задачу.
Заданы диаметр D дисковой фрезы c числом зубьев z и задний угол заточки зуба α.
Вычислить угол затылования φ и эксцентриситет ε установки инструмента относительно заточного круга. При расчете параметров φ и ε учесть, что при затыловании по дуге эксцентрической окружности каждый зуб инструмента обрабатывается индивидуально.
Для решения такой задачи необходимо знание математической модели взаимосвязей параметров затылования с величиной заднего угла α и радиусом R затылуемого инструмента.
Математическая модель. На основании понятий высшей математики о геометрическом смысле производной функции и представления функций в полярной системе координат в работе [1] построена следующая математическая модель взаимосвязей параметров затылования с величиной заднего угла α и радиусом R затылуемого инструмента
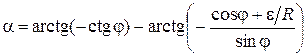 ,
,
в которой R - радиус дисковой фрезы.
Полученное уравнение является трансцендентным и определение параметров затылования φ иε представляет собой чисто математическую задачу решения приведенного выше нелинейного уравнения.
Задание
1. Выбрать численный метод решения математической модели параметров ориентации в пространстве перезатачиваемого инструмента относительно заточного круга. Привести обоснование выбора метода.
2. Выполнить постановку вычислительной задачи. Разработать алгоритм реализации численного метода на ЭВМ.
3. Составить тест отладки программы расчета параметров затылования, приняв в качестве исходных данных следующие значения входных параметров:
- диаметр дисковой фрезы 2R = 80 мм;
- число зубьев фрезы z = 12;
- задний угол заточки зуба α = 15°.
Примечание. При расчете параметров φ и ε учесть, что при затыловании по дуге эксцентрической окружности каждый зуб инструмента обрабатывается индивидуально. Поэтому угол поворота φ радиуса Rи, на котором лежит центр затылуемой окружности не может быть больше 360°/2z для избежания нежелательного касания необрабатываемого зуба заточным кругом.
Литература
1. Свидерский Э.А. Решение технических задач в машиностроении с применением микрокалькуляторов. – М.: Машиностроение, 1987. – 160с.
Тема №2
Задача расчета параметров схемы затылования
металлорежущего инструмента по дуге гипотрохоиды.
 |
Постановка задачи. Для получения режущего клина на зубе инструмента осуществляют его заточку с образованием заднего угла α (рис. 1). Это угол между касательной mо к окружности, проходящей через вершину зуба и имеющей центр на оси вращения инструмента, и касательной mз к задней поверхности в той же точке инструмента (вершине зуба).
Существует несколько способов образования заднего угла. Самым простым способом является заточка инструмента по прямой линии (рис. 1, а). Этот способ позволяет произвести заточку инструмента по задней поверхности без использования каких-либо специальных приспособлений. Однако образованный таким способом режущий клин не восстанавливается при перезаточке инструмента по мере износа. Кроме того, при заточке по прямой линии происходит ослабление вершины зуба. Поэтому у тяжелонагруженного фасонного инструмента заднюю поверхность зуба выполняют по дугам сложных кривых (затылуют) – по спирали Архимеда, дуге эксцентрической окружности, дуге гипотрохоиды (рис. 1, б, в, г). Это предоставляет возможность при образовании на задней поверхности зуба инструмента площадки износа с нулевым задним углом переточить инструмент с образованием плоскости на передней поверхности зуба. При этом практически восстанавливается исходный задний угол.
Затылование по дугам кривых требует строгой ориентации в пространстве перезатачиваемого инструмента относительно заточного (шлифовального круга), а также согласования движений обрабатываемого и обрабатывающего инструментов во времени и пространстве. Затылование режущего инструмента по дуге гипотрохоиды (укороченной гипоциклоиды) кинематически реализуется вращением затачиваемого инструмента вокруг двух параллельных осей О1 и О2 с различными по величине и направлению угловыми скоростями ω1 и ω2 (рис. 2), причем отношение угловых скоростей должно быть равно числу зубьев затылуемого инструмента, т. е. 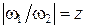 .
.
Из геометрического представления схемы затылования инструмента по гипотрохоиде можно заметить, что величина заднего угла α зависит от угла φ установки вершины зуба инструмента относительно вершины гипотрохоиды и кривизны ее ветви в данной точке. Радиус кривизны гипотрохоиды, в свою очередь, зависит от величины эксцентриситета ε – расстояния между осями О1 и О2.
 Таким образом, для выполнения операции затылования зуба инструмента по дуге гипотрохоиды с образованием заданного заднего угла α должны быть определены параметры φ и ε ориентации в пространстве перезатачиваемого инструмента относительно заточного (шлифовального круга), а также согласования движений обрабатываемого инструмента во времени и пространстве, решив следующую задачу.
Таким образом, для выполнения операции затылования зуба инструмента по дуге гипотрохоиды с образованием заданного заднего угла α должны быть определены параметры φ и ε ориентации в пространстве перезатачиваемого инструмента относительно заточного (шлифовального круга), а также согласования движений обрабатываемого инструмента во времени и пространстве, решив следующую задачу.
Заданы диаметр D дисковой фрезы c числом зубьев z и задний угол заточки зуба α.
Вычислить угол φ установки вершины зуба инструмента относительно вершины гипотрохоиды и эксцентриситет ε между осями О1 и О2 вращения инструмента.
Для решения такой задачи необходимо знание математической модели взаимосвязей параметров затылования с величиной заднего угла α, числом зубьев и радиусом R затылуемого инструмента.
Математическая модель. На основании понятий высшей математики о геометрическом смысле производной функции и представления функций в полярной системе координат в работе [1] построена следующая математическая модель взаимосвязей параметров затылования с величиной заднего угла α и радиусом R затылуемого инструмента
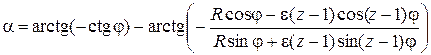 ,
,
в которой R - радиус дисковой фрезы.
Полученное уравнение является трансцендентным и определение параметров затылования φ иε представляет собой чисто математическую задачу решения приведенного выше нелинейного уравнения.
Задание
1. Выбрать численный метод решения математической модели параметров ориентации в пространстве перезатачиваемого инструмента относительно заточного круга. Привести обоснование выбора метода.
2. Выполнить постановку вычислительной задачи. Разработать алгоритм реализации численного метода на ЭВМ.
3. Составить тест отладки программы расчета параметров затылования, приняв в качестве исходных данных следующие значения входных параметров:
- диаметр дисковой фрезы 2R = 80 мм;
- число зубьев фрезы z = 12;
- задний угол заточки зуба α = 15°.
Литература
1. Свидерский Э.А. Решение технических задач в машиностроении с применением микрокалькуляторов. – М.: Машиностроение, 1987. – 160с.
Тема №3
Задача расчета торцового размера по роликам для контроля точности
изготовления прямозубых колес с нечетным числом зубьев
Существенное повышение качества выпускаемых изделий машиностроения достигается наряду с совершенствованием методов механической обработки деталей и металлообрабатывающего инструмента, совершенствованием способов и средств контроля показателей качества деталей. Нередко при разработке методик контроля точности размеров изготовленных деталей возникают задачи, решение которых требует применение методов вычислительной математики. В частности, такие задачи имеют место при определении номинальных значений торцового размера по шарикам (роликам) для контроля точности изготовления зубчатых колес внешнего (внутреннего) зацепления с четным (нечетным) числом зубьев. Одна из таких задач предложена для решения в данной теме курсовой работы.
 Постановка задачи. Разрабатывается технологический процесс изготовления прямозубого цилиндрического колеса внешнего зацепления с нечетным числом зубьев. В технологическом процессе, наряду с операциями механической обработки, предусматривается контроль точности изготовления зубчатых колес. Определен контролируемый показатель точности обработки - торцовый размер M по роликам, вложенным в противоположные впадины зубчатого колеса (рис. 1).
Постановка задачи. Разрабатывается технологический процесс изготовления прямозубого цилиндрического колеса внешнего зацепления с нечетным числом зубьев. В технологическом процессе, наряду с операциями механической обработки, предусматривается контроль точности изготовления зубчатых колес. Определен контролируемый показатель точности обработки - торцовый размер M по роликам, вложенным в противоположные впадины зубчатого колеса (рис. 1).
Заданы значения входных параметров и условия установки обрабатывающего режущего инструмента, к которым относятся:
- m – модуль зубчатого колеса;
- z – число зубьев;
- D – диаметр ролика;
- x – коэффициент смещения исходного производящего контура инструмента относительно обрабатываемого зубчатого колеса.
Вычислить номинальное значение торцового размера M по роликам для контроля точности изготовления прямозубого цилиндрического колеса внешнего зацепления с нечетным числом зубьев.
Для решения такой задачи необходимо знание математической модели взаимосвязей размера M с входными параметрами и условием установки обрабатывающего режущего инструмента.
Математическая модель. В данной задаче математическая модель контролируемого торцового размера M может быть построена, исходя из геометрической модели этого параметра (рис. 1) и основных понятий теории механизмов и машин.
Так из геометрических построений, приведенных на рис. 1 имеем
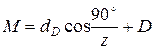 ,
,
где z – число зубьев колеса; D – диаметр ролика; dD – диаметр окружности, проходящей через центры вложенных во впадины колеса роликов. Определяется по формуле
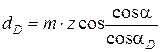 ,
,
в которой:
m – модуль зубчатого колеса;
α – угол главного профиля;
αD – угол профиля зуба на окружности dD; находится из решения уравнения
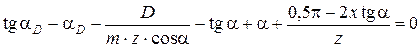 ,
,
где x – коэффициент смещения исходного производящего контура инструмента относительно обрабатываемого зубчатого колеса.
Полученное уравнение является трансцендентным и определение угла профиля αD зуба представляет собой чисто математическую задачу решения приведенного выше нелинейного уравнения.
Задание
1. Выбрать численный метод решения математической модели угла профиля αD зуба. Привести обоснование выбора метода.
2. Выполнить постановку вычислительной задачи. Разработать алгоритм реализации численного метода на ЭВМ.
3. Составить тест отладки программы для расчета угла профиля αD зуба, приняв в качестве исходных данных следующие значения входных параметров:
– модуль зубчатого колеса, m = 6 мм;
– число зубьев, z = 27;
– диаметр ролика, D = 10,353 мм;
– коэффициент смещения исходного производящего контура инструмента относительно обрабатываемого зубчатого колеса, x = 0,3.
4. Для полученного значения угла αD рассчитать торцовый размер по роликам M зубчатого колеса.
Тема №4
Задача определения параметров эмпирической зависимости
скорости резания при токарной обработке
Экспериментальными исследованиями установлено, что при продольной обточке заготовок скорость резания v может быть определена по эмпирической зависимости вида
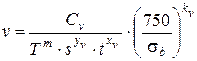 ,
,
в которой: T – стойкость инструмента, мин; s – подача, мм/об; t – глубина резания, мм; σb – предел прочности обрабатываемого материала, МПа; Cv, m, yv, xv, kv – коэффициент и показатели степеней, значения которых находятся по результатам экспериментов, выполненных для конкретных числовых данных факторов T, s, t, и σb режима обработки.
К сожалению, использование вышеприведенной зависимости для скорости резания допускается только для тех значений факторов режима обработки, при которых были получены величины Cv, m, yv, xv и kv. В случае необходимости выбора условий обработки, выходящих за пределы исследованных, возникает задача определения значений параметров Cv, m, yv, xv и kv для новых заданных условий обработки.
Является естественным, что для уменьшения трудоемкости обработки опытных данных каждого нового эксперимента по определению значений параметров Cv, m, yv, xv и kv в приведенной зависимости необходимо иметь программу решения этой задачи на ЭВМ и соответствующий тест проверки ее работоспособности.
Постановка задачи. Выполнен эксперимент для определения значений параметров Cv , m , yv , xv и kv формулы вычисления скорости резания при продольном точении заготовок из стали 40Х. Исследуемые режимы обработки и усредненные результаты измерений скорости резания в каждом опыте приведены в следующей таблице:
Таблица
| Номер опыта, i | Ti, мин | ti, мм | si, мм/об | σbi, МПа | vi, м/мин |
| 1 | 60 | 2,0 | 0,08 | 750 | 100,0 |
| 2 | 45 | 1,7 | 0,10 | 700 | 111,3 |
| 3 | 60 | 1,5 | 0,15 | 650 | 119,4 |
| 4 | 30 | 2,0 | 0,20 | 800 | 77,1 |
| 5 | 45 | 1,8 | 0,20 | 850 | 67,7 |
Определить параметры Cv, m, yv, xv и kv в формуле скорости резания
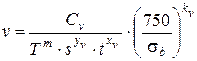 (1).
(1).
Разработка математической модели. Для построения математической модели, отражающей взаимосвязи искомых параметров Cv, m, yv, xv и kv с факторами режима точения и скоростью резания выполним следующие преобразования эмпирической зависимости (1):
а) прологарифмируем выражения левой и правой части этой зависимости. Получим
 ; (2)
; (2)
б) подставим из таблицы значения факторов T, s, t, и σb режима обработки и скорости резания v в каждом i –м опыте в формулу (2). При этом получим систему из n уравнений с неизвестными величинами Cv, m, yv, xv и kv. В поставленной задаче n = 5.
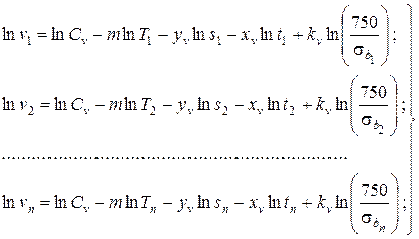 (3)
(3)
в) введя в уравнениях (3) общепринятые в математике обозначения для искомых величин Cv, m, yv, xv и kv через xi, т. е. 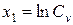 ,
, 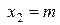 ,
, 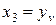 ,
, 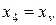 ,
, 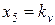 и обозначив через коэффициенты aij величины:
и обозначив через коэффициенты aij величины: 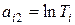 ,
, 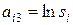 ,
, 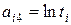 ,
, 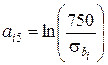 и через bi – величину
и через bi – величину 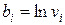 , система (3) примет вид
, система (3) примет вид
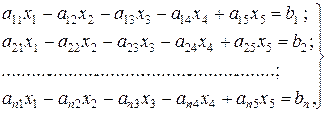 (4)
(4)
где 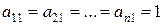 .
.
Таким образом, поставленная выше технологическая задача представляет собой известную в вычислительной математике задачу нахождения решения системы из n линейных алгебраических уравнений с n неизвестными.
Задание
1. Выбрать метод решения математической модели параметров Cv, m, yv, xv и kv. Привести обоснование выбора метода.
2. Выполнить постановку вычислительной задачи. Разработать алгоритм реализации численного метода на ЭВМ.
3. Используя приведенные в таблице данные, составить тест отладки программы для расчета Cv, m, yv, xv и kv.
Замечание. Следует учитывать, что найденное значение корня x1 системы уравнений (4) является значением 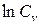 . Поэтому при разработке алгоритма решения задачи и составлении теста следует предусмотреть вычисление Cv = exp x1.
. Поэтому при разработке алгоритма решения задачи и составлении теста следует предусмотреть вычисление Cv = exp x1.
Тема № 5
Задача определения параметров эмпирической зависимости
силы резания при токарной обработке
Экспериментальными исследованиями установлено, что при продольной обточке заготовок тангенциальная сила резания Pz может быть определена по эмпирической зависимости вида
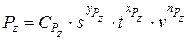 ,
,
в которой: v – скорость резания, м/мин; s – подача, мм/об; t – глубина резания, мм; 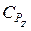 ,
, 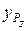 ,
, 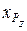 ,
, 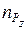 – коэффициент и показатели степеней, значения которых находятся по результатам экспериментов, выполненных для конкретных значений факторов v, s, t, режима обработки.
– коэффициент и показатели степеней, значения которых находятся по результатам экспериментов, выполненных для конкретных значений факторов v, s, t, режима обработки.
К сожалению, использование вышеприведенной зависимости для силы резания допускается только для тех значений факторов режима обработки, при которых были получены величины 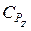 ,
, 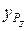 ,
, 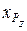 ,
, 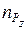 . В случае необходимости выбора режима обработки, выходящих за пределы исследованных, возникает задача определения новых значений параметров
. В случае необходимости выбора режима обработки, выходящих за пределы исследованных, возникает задача определения новых значений параметров 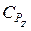 ,
, 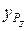 ,
, 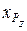 ,
, 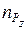 .
.
Является естественным, что для уменьшения трудоемкости обработки опытных данных каждого нового эксперимента по определению значений параметров 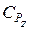 ,
, 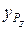 ,
, 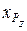 ,
, 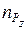 в приведенной зависимости необходимо иметь программу решения этой задачи на ЭВМ и соответствующий тест проверки ее работоспособности.
в приведенной зависимости необходимо иметь программу решения этой задачи на ЭВМ и соответствующий тест проверки ее работоспособности.
Постановка задачи. Выполнен эксперимент для определения значений параметров 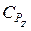 ,
, 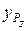 ,
, 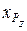 ,
, 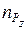 формулы вычисления тангенциальной силы резания при продольном точении стальных заготовок. Исследуемые режимы обработки и усредненные результаты измерений силы резания в каждом опыте приведены в следующей таблице:
формулы вычисления тангенциальной силы резания при продольном точении стальных заготовок. Исследуемые режимы обработки и усредненные результаты измерений силы резания в каждом опыте приведены в следующей таблице:
Таблица
| Номер опыта, i | vi, м/мин | ti, мм | si, мм/об | 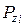 , Н , Н
|
| 1 | 60,0 | 2,8 | 0,8 | 3772 |
| 2 | 45,0 | 3,2 | 1,0 | 5219 |
| 3 | 70,0 | 2,5 | 0,9 | 3572 |
| 4 | 90,0 | 1,7 | 1,0 | 2674 |
Определить параметры 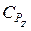 ,
, 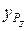 ,
, 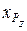 ,
, 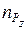 в формуле силы резания
в формуле силы резания
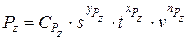 . (1).
. (1).
Разработка математической модели. Для построения математической модели, отражающей взаимосвязи искомых параметров 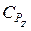 ,
, 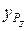 ,
, 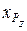 ,
, 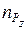 с факторами режима точения и силой резания выполним следующие преобразования эмпирической зависимости (1):
с факторами режима точения и силой резания выполним следующие преобразования эмпирической зависимости (1):
а) прологарифмируем выражения левой и правой части этой зависимости. Получим
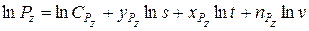 ; (2)
; (2)
б) подставим из таблицы значения факторов s, t, и v режима обработки и силы резания Pz в каждом i –м опыте в формулу (2). При этом получим систему из n уравнений с неизвестными величинами 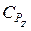 ,
, 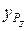 ,
, 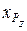 ,
, 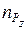 . В поставленной задаче n = 4.
. В поставленной задаче n = 4.
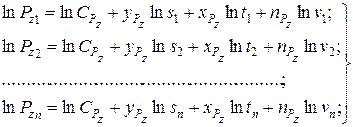 (3)
(3)
в) введя в уравнениях (3) общепринятые в математике обозначения для искомых величин 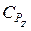 ,
, 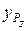 ,
, 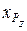 ,
, 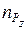 через xi, т. е.
через xi, т. е. 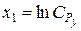 ,
, 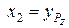 ,
, 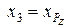 ,
, 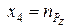 и обозначив через коэффициенты aij величины:
и обозначив через коэффициенты aij величины: 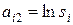 ,
,  ,
, 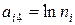 и через bi – величину
и через bi – величину 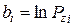 , система (3) примет вид
, система (3) примет вид
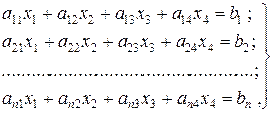 (4)
(4)
где 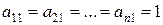 .
.
Таким образом, поставленная выше технологическая задача представляет собой известную в вычислительной математике задачу нахождения решения системы из n линейных алгебраических уравнений с n неизвестными.
Задание
1. Выбрать метод решения математической модели параметров 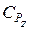 ,
, 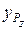 ,
, 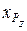 ,
, 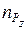 . Привести обоснование выбора метода.
. Привести обоснование выбора метода.
2. Выполнить постановку вычислительной задачи. Разработать алгоритм реализации численного метода на ЭВМ.
3. Используя приведенные в таблице данные, составить тест отладки программы для расчета 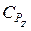 ,
, 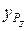 ,
, 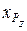 ,
, 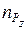 .
.
Замечание. Следует учитывать, что найденное значение корня x1 системы уравнений (4) является значением 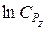 . Поэтому при разработке алгоритма решения задачи и составлении теста следует предусмотреть вычисление
. Поэтому при разработке алгоритма решения задачи и составлении теста следует предусмотреть вычисление 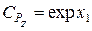 .
.
Тема № 6
Задача определения площади контакта инструмента и заготовки при обкатывании торовым роликом
Обкатыванием называется процесс пластического деформирования металла поверхностного слоя детали инструментом (шаром, роликом) при его качении по обрабатываемой поверхности. Обкатывание производится с целью уменьшения шероховатости, упрочнения поверхностного слоя, повышения точности размеров и формы деталей. Подвергаемая обкатыванию поверхность предварительно обрабатывается точением, шлифованием и другими методами обработки резанием.
Изучение механики пластического деформирования металла поверхностного слоя детали при обкатывании проводится для выявления сущности контактных явлений, определения оптимальных режимов обкатывания, обеспечивающих заданные значения показателей качества поверхности и, следовательно, требуемые эксплуатационные свойства детали.
Одним из направлений исследования процесса обкатывания является исследование геометрических параметров контактного взаимодействия инструмента с обрабатываемой поверхностью. В частности, знание площади контакта инструмента с обрабатываемой поверхностью заготовки позволяет рассчитать силы, действующие на инструмент, произвести анализ тепловых явлений, прогнозировать процесс износа инструмента.
При обкатывании плоских поверхностей роликом в виде тора область контакта имеет сложную форму и зависит от взаимного положения осей обрабатываемой поверхности и торового ролика (см. рис.).
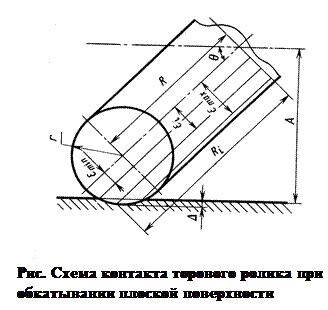 Постановка задачи. В проектируемом технологическом процессе изготовления деталей типа дисков в качестве финишной операции обработки их торцовых поверхностей выбрано обкатывание торовым роликом, обеспечивающее высокую производительность обработки и упрочнение поверхностного слоя. Основным параметром режима обкатывания является сила прижатия ролика к обрабатываемой поверхности. Выбор силы производится, исходя из требуемого контактного давления и величины площади контакта ролика с обкатываемой деталью. Поэтому предварительно рассчитывается площадь контакта, считая известными его размеры, величину внедрения в обрабатываемую поверхность и угол наклона ролика к поверхности обработки. Расчет производят, решая следующую математическую модель площади контакта.
Постановка задачи. В проектируемом технологическом процессе изготовления деталей типа дисков в качестве финишной операции обработки их торцовых поверхностей выбрано обкатывание торовым роликом, обеспечивающее высокую производительность обработки и упрочнение поверхностного слоя. Основным параметром режима обкатывания является сила прижатия ролика к обрабатываемой поверхности. Выбор силы производится, исходя из требуемого контактного давления и величины площади контакта ролика с обкатываемой деталью. Поэтому предварительно рассчитывается площадь контакта, считая известными его размеры, величину внедрения в обрабатываемую поверхность и угол наклона ролика к поверхности обработки. Расчет производят, решая следующую математическую модель площади контакта.
Математическая модель. При построении модели области контакта торового ролика с обрабатываемой поверхностью полагали [1]:
1) ролик выполнен из абсолютно жесткого материла;
2) обрабатываемая поверхность идеально плоская;
3) упругие деформации материала поверхности детали пренебрежимо малы по сравнению с пластическими;
4) площадь контакта практически равна площади проекции области контакта на плоскость, параллельную обрабатываемой поверхности.
Исходя из геометрии схемы контакта тора с плоской поверхностью и используя аппарат начертательной геометрии, были получены следующие формулы, описывающие форму области контакта тора:
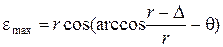 ;
; 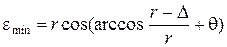 ; (1)
; (1)
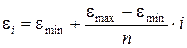 ; (2)
; (2)
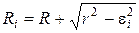 ; (3)
; (3)
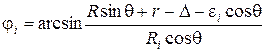 ; (4)
; (4)
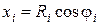 ; (5)
; (5)
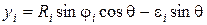 . (6)
. (6)
В этих формулах:
r – радиус тора, мм;
Δ – величина внедрения тора в обрабатываемую поверхность, мм;
θ – угол наклона торового ролика к поверхности обработки, рад;
R – радиус от центра вращения до оси тора, мм;
εi – текущее значение расстояния секущей плоскости ролика от его оси симметрии (см. рис.);
εmax, εmin – максимальное и минимальное расстояния от оси симметрии тора до его крайних сечений, контактирующих с поверхностью обработки, мм;
Ri – текущее значение радиуса окружности тора в его сечении плоскостью на расстоянии εi от оси симметрии, мм;
φi – текущее значение параметра, определяющего угловое расстояние от оси φ до места контакта торового круга в сечении εi с плоскостью (поверхностью) обработки, рад;
xi, yi – текущие координаты точек контура области контакта, мм;
n – число текущих координат xi, yi (задается, исходя из требуемой точности вычисления площади контакта).
Формулы (4)-(6), с использованием которых должна вычисляться площадь области контакта торового ролика с обкатываемой поверхностью, являются функциями от параметра εi, вычисляемого по выражению (2).
Так как непосредственно выразить в аналитической форме зависимость площади контакта с использованием формул (4)-(6) не представляется возможным, вычисление площади контакта осуществляется численным методом интегрирования функций. В работе [1] предложено вычислять площадь контакта методом трапеций, формула которого при задании подынтегральной функции параметрическими уравнениями (4)-(6) имеет вид:
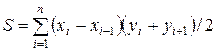 . (7)
. (7)
Требуемая точность вычисления площадь контакта достигается при задании числа n текущих координат xi, yi.
Таким образом, поставленная технологическая задача вычисления площади контакта торового ролика с обрабатываемой поверхностью сведена к задаче вычислительной математики интегрирования функций численным методом, в данном случае методом трапеций.
Задание
1. Произвести постановку вычислительной задачи вычисления площади контакта торового ролика с обрабатываемой поверхностью. Разработать алгоритм реализации численного метода на ЭВМ.
2. Составить тест отладки программы расчета площади контакта, приняв в качестве исходных данных следующие значения входных параметров:
- радиус тора r = 5 мм;
- радиус от центра вращения до оси тора R = 50 мм;
- величина внедрения тора в обрабатываемую поверхность Δ = 15мм;
- угол наклона торового ролика к поверхности обработки θ = 20°.
- число текущих координат xi, yi n = 4.
Литература
2. Сургунт Я.М., Свидерский Э.А., Котиков П.Ф. К определению площади пятна контакта торового ролика и поверхности // IV Республиканская научно-техническая конференция «Автоматический контроль и управление производственными процессами». Минск, 1983. 123с.
3. Свидерский Э.А. Решение технических задач в машиностроении с применением микрокалькуляторов. – М.: Машиностроение, 1987. – 160с.
Тема № 7
Задача определения параметров площадки контакта абсолютно твердого шара при внедрении в цилиндрическую поверхность тела
При определении механических свойств материалов, проектировании различных технических устройств и разработке способов механической обработки деталей, в частности, методами поверхностного пластического деформирования, возникает задача о контакте двух тел (так называемая контактная задача). В самом общем случае контактная задача формулируется в следующем виде.
Пусть имеются два тела, ограниченные нелинейными поверхностями, первоначально соприкасающиеся в точке. К ним приложена сила их сжатия, действующая в направлении нормали, проходящей через точку касания тел. Возникает ряд вопросов:
- на какую величину сблизятся тела при их сжатии;
- какие деформации материала возникнут в области контакта тел;
- какую форму имеет область контакта тел и др.
Результаты исследования этих вопросов имеют практическую ценность для определения несущей способности деталей машин и механизмов, выбора режима обработки деталей методами пластического деформирования, выявления механизма формирования качества поверхностного слоя деталей и т. п.
Постановка задачи. Согласно требованиям ГОСТ 9012-59 90 (ИСО 410 82, ИСО 6506-81) измерение твердости материала по Бринеллю производится путем вдавливания шарика (стального или из твердого сплава) под действием заданной силы, приложенной перпендикулярно к плоской поверхности образца. При этом на образце образуется отпечаток, ограниченный окружностью, по величине диаметра которой определяется твердость материала. Однако нередко измерение твердости материала детали приходится выполнять вдавливанием шарика в цилиндрическую поверхность детали. Возникают вопросы, какую геометрическую форму имеет пластический отпечаток при внедрении шара в цилиндрическую поверхность детали, как оценить твердость материала, если пластический отпечаток имеет контур, отличный от окружности.
В определенной степени ответы на эти вопросы могут быть получены решением контактной задачи теории упругости, в которой построена математическая модель взаимосвязей геометрических параметров области контакта и контактируемых тел и силы их сжатия.
Математическая модель контакта двух упругих тел. При сжатии двух тел, ограниченных нелинейными поверхностями с приведенными радиусами кривизны R1 и R2 в главных нормальных сечениях, они будут взаимодействовать не в одной точке их первоначального касания, а по некоторому малому участку их поверхностей. Этот участок их взаимодействия называется площадкой контакта, а ограничивающая ее кривая – контуром площадки контакта. Установлено [1], что при упругом сжатии тел, поверхность их контакта представляет собой эллиптическую площадку с эксцентриситетом е. Последний находится из решения уравнения:
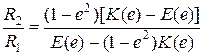 , (1)
, (1)
в котором K(е)и Е(е) – эллиптические интегралы первого и второго рода
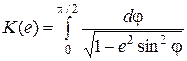 ,
, 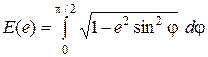 ; (2)
; (2)
1/R1, 1/R2 – приведенные кривизны поверхностей тел в точке их касания 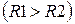 .
.
При внедрении штампа (абсолютно жесткого тела) со сферическим основанием радиусом r в цилиндрическую поверхность радиусом R упругого тела полуоси a и b их эллиптической площадки контакта определяются по формулам:
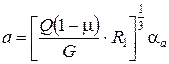 ,
, 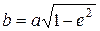 , (3)
, (3)
где 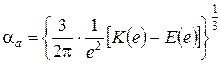 ; Q – сила сжатия тел, Н; R1 – наибольший из радиусов приведенных кривизн 1/R1, 1/R2 поверхностей тел в точке их первоначального касания, мм:
; Q – сила сжатия тел, Н; R1 – наибольший из радиусов приведенных кривизн 1/R1, 1/R2 поверхностей тел в точке их первоначального касания, мм: 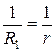 ,
, 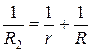 ;
;
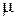 – коэффициент Пуассона материала деформируемого тела; G – модуль сдвига материала, Н/мм2.
– коэффициент Пуассона материала деформируемого тела; G – модуль сдвига материала, Н/мм2.
Задание
1. Выполнить вычислительный эксперимент по исследованию площади контакта при внедрении штампа со сферическим основанием радиусом r в поверхность упругого тела при следующих условиях:
а) упругое тело ограничено цилиндрической поверхностью радиусом R;
б) упругое тело ограничено плоской поверхностью.
Сила давления штампа Q = 1000 Н; G = 80925 Н/мм2; µ = 0,35; r = 5 мм; R = 20 мм.
2. Произвести постановку вычислительной задачи вычисления интегралов K(е)и Е(е) методом Гаусса. Разработать алгоритм реализации численного метода на ЭВМ. Привести все вычисления разработки теста для одного из интегралов.
Литература
1. Лурье А.И. Теория упругости. М.: Наука, 1970. – 940с.
Тема № 8
Моделирование на ЗВМ процесса вибраций инструмента
при алмазном выглаживании
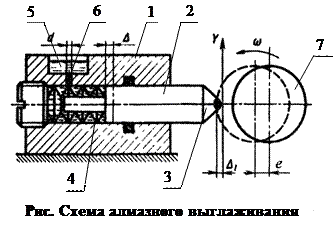 Для уменьшения величины неровностей (шероховатости) поверхности и её упрочнения применяют алмазное выглаживание, которое осуществляется по схеме точения с помощью приспособления, устанавливаемого в резцедержателе токарного станка (см. рис.). Приспособление состоит из корпуса 1, в который с возможностью свободного поступательного перемещения вставлен шток 2 с закреплённым в нём выглаживателем 3. Для создания требуемой силы прижатия выглаживателя к обрабатываемой поверхности служит упругий элемент 4, выполненный в виде пружины. Приспособление имеет демпферный механизм, представляющий собой две полости, заполненные маслом 5 и соединённые между собой каналом 6. Функцию поршня в этом механизме выполняет шток 2.
Для уменьшения величины неровностей (шероховатости) поверхности и её упрочнения применяют алмазное выглаживание, которое осуществляется по схеме точения с помощью приспособления, устанавливаемого в резцедержателе токарного станка (см. рис.). Приспособление состоит из корпуса 1, в который с возможностью свободного поступательного перемещения вставлен шток 2 с закреплённым в нём выглаживателем 3. Для создания требуемой силы прижатия выглаживателя к обрабатываемой поверхности служит упругий элемент 4, выполненный в виде пружины. Приспособление имеет демпферный механизм, представляющий собой две полости, заполненные маслом 5 и соединённые между собой каналом 6. Функцию поршня в этом механизме выполняет шток 2.
При обработке деталей выглаживатель прижимают к обрабатываемой поверхности с заданной упругим элементом 4 силой F , в результате между выглаживателем и поверхностью детали создаётся предварительный натяг 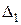 (внедрение инструмента), величина которого обеспечивает требуемую степень сглаживания неровностей поверхности и её упрочнение.
(внедрение инструмента), величина которого обеспечивает требуемую степень сглаживания неровностей поверхности и её упрочнение.
 Установлено, что эффективность алмазного выглаживания зависит не только от параметров режима обработки (силы выглаживания, скорости обработки, подачи), но и характеристик системы «станок – приспособление – инструмент - заготовка» (СПИЗ). В частности, при обработке заготовки, установленной в центрах с биением e, вследствие периодически изменяющейся силы выглаживания, в системе СПИЗ возникают вибрации, приводящие к резкому ухудшению качества обрабатываемой поверхности. Является очевидным, что для управления колебательным процессом, возникающим при выглаживании, необходимо знание характеристик этого процесса.
Установлено, что эффективность алмазного выглаживания зависит не только от параметров режима обработки (силы выглаживания, скорости обработки, подачи), но и характеристик системы «станок – приспособление – инструмент - заготовка» (СПИЗ). В частности, при обработке заготовки, установленной в центрах с биением e, вследствие периодически изменяющейся силы выглаживания, в системе СПИЗ возникают вибрации, приводящие к резкому ухудшению качества обрабатываемой поверхности. Является очевидным, что для управления колебательным процессом, возникающим при выглаживании, необходимо знание характеристик этого процесса.
Содержательная постановка задачи. Выполнить моделирование колебательного движения инструмента при выглаживании в условиях биения обрабатываемой поверхности. Определить характеристики упругого элемента и демпфера приспособления, при которых происходит отрыв выглаживателя от поверхности заготовки при заданном режиме обработке. Сопрягаемые поверхности штока и корпуса приспособления считаются гладкими.
Математическая модель колебательного движения инструмента. Величина внедрения d выглаживателя при обработке в условиях колебательного процесса в системе «станок- приспособление- инструмент-заготовка» может быть определена по формуле [1]
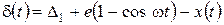 , (1)
, (1)
в которой перемещение x(t)выглаживателя определяется из решения дифференциального уравнения
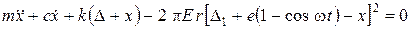 (2)
(2)
с начальными условиями
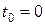 ;
; 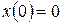 ;
; 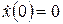 , (3)
, (3)
где: 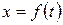 – искомая функция, описывающая перемещение инструмента в зависимости от времени обработки, мм; m – приведённая масса движущихся частей, равная массе инструмента с подвижными частями приспособления и 1/3 массы пружины, кг; c – коэффициент демпфирования, Н/(мм/с); k – жёсткость пружины, Н/мм;
– искомая функция, описывающая перемещение инструмента в зависимости от времени обработки, мм; m – приведённая масса движущихся частей, равная массе инструмента с подвижными частями приспособления и 1/3 массы пружины, кг; c – коэффициент демпфирования, Н/(мм/с); k – жёсткость пружины, Н/мм; 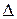 – предварительный натяг пружины, мм; e – величина биения детали, мм; E – жёсткость материала обрабатываемой детали на единицу объёма деформирования, Н/мм3;
– предварительный натяг пружины, мм; e – величина биения детали, мм; E – жёсткость материала обрабатываемой детали на единицу объёма деформирования, Н/мм3; 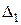 – исходная глубина внедрения инструмента в деталь, мм; r – радиус рабочей части выглаживателя, мм; w – угловая скорость вращения детали, рад/с.
– исходная глубина внедрения инструмента в деталь, мм; r – радиус рабочей части выглаживателя, мм; w – угловая скорость вращения детали, рад/с.
Таким образом, технологическая задача о вибрациях инструмента при алмазном выглаживании представляет собой математическую задачу Коши решения дифференциального уравнения (2) с начальными условиями (3).
Задание
1. Исследовать на ЭВМ изменение величины внедрения выглаживателя при обработке детали, установленной с биением обрабатываемой поверхности, в зависимости от угловой скорости вращения детали.
Исходные данные: m = 0,25 кг; c = 200 H/(мм/с); e = 0,05 мм; 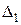 = 0,01 мм; c = 50 Н/мм;
= 0,01 мм; c = 50 Н/мм; 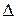 = 4 мм; E = 2,5·103 Н/мм3; w = 20, 40, 60, 80, 100 c-1. Интервал времени исследования процесса
= 4 мм; E = 2,5·103 Н/мм3; w = 20, 40, 60, 80, 100 c-1. Интервал времени исследования процесса 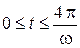 .
.
2. При разработке алгоритма и программы моделирования колебательного процесса использовать метод Рунге-Кутта IV порядка для вычисления значений величины перемещения инструмента. Для тестирования программного модуля решения дифференциального уравнения достаточно иметь контрольные значения перемещения инструмента в двух-трёх точках начального участка интервала интегрирования уравнения для одного из значений w, например, w = 60 с-1.
Литература
1. Моделирование технических объектов на макроуровне: Метод. указания. /А.С. Донсков: Перм. гос. техн. ун-т. Пермь, 2007. – 24 с.
Тема № 9
Задача интерполирования геометрических параметров области контакта
при упругом сжатии двух тел
При определении механических свойств материалов, проектировании различных технических устройств и разработке способов механической обработки деталей, в частности, методами поверхностного пластического деформирования, возникает необходимость решения задачи о контакте двух тел (так называемой контактной задачи). В самом общем случае контактная задача формулируется в следующем виде.
Пусть имеются два тела, ограниченные нелинейными поверхностями, первоначально соприкасающимися в точке. К ним приложена сила сжатия, действующая в направлении нормали к граничным поверхностям тел, проходящей через точку их касания.
Какие напряжения и деформации возникают в сжатых телах в точках окрестности их контакта.
Результаты решения контактной задачи имеют практическую ценность для определения несущей способности деталей машин и механизмов, выбора режима обработки деталей методами пластического деформирования, выявления механизма формирования качества поверхностного слоя деталей и т. п.
В настоящее время всесторонне изучена контактная задача для случая упругого сжатия тел и на основе математического аппарата теории упругости получены математические модели, отражающие различные стороны взаимодействия двух тел при их сжатии. В частности, построена математическая модель геометрических параметров области контакта при сжатии двух упругих тел, которая имеет следующий вид.
Математическая модель контакта двух упругих тел. При сжатии двух тел, ограниченных нелинейными поверхностями с радиусами кривизны 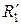 ,
, 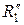 и
и 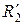 ,
, 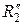 в главных нормальных сечениях, они будут взаимодействовать не в одной точке их первоначального касания, а по некоторому малому участку их поверхностей. Этот участок их взаимодействия называется площадкой контакта, а ограничивающая ее кривая – контуром площадки контакта. Установлено [1], что при упругом сжатии тел, поверхность их контакта представляет собой эллиптическую площадку с эксцентриситетом е, который находится из решения уравнения:
в главных нормальных сечениях, они будут взаимодействовать не в одной точке их первоначального касания, а по некоторому малому участку их поверхностей. Этот участок их взаимодействия называется площадкой контакта, а ограничивающая ее кривая – контуром площадки контакта. Установлено [1], что при упругом сжатии тел, поверхность их контакта представляет собой эллиптическую площадку с эксцентриситетом е, который находится из решения уравнения:
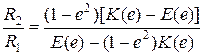 , (1)
, (1)
в котором K(е)и Е(е) – эллиптические интегралы первого и второго рода
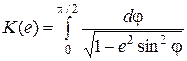 ,
, 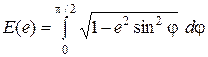 ; (2)
; (2)
1/R1, 1/R2 – приведенные кривизны поверхностей тел в точке их касания 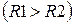 .
.
По найденному значению эксцентриситета эллиптической площадки контакта в дальнейшем вычисляются ее большая a и малая b полуоси по формулам:
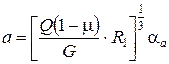 ,
, 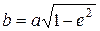 , (3)
, (3)
где 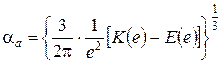 ; Q – сила сжатия тел;
; Q – сила сжатия тел; 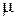 – коэффициент Пуассона материала деформируемого тела; G – модуль сдвига материала; R1 – наибольший из радиусов приведенных кривизн 1/R1, 1/R2 поверхностей тел в точке их первоначального касания.
– коэффициент Пуассона материала деформируемого тела; G – модуль сдвига материала; R1 – наибольший из радиусов приведенных кривизн 1/R1, 1/R2 поверхностей тел в точке их первоначального касания.
Приведенные кривизны 1/R1, 1/R2 поверхностей тел в точке их первоначального касания зависят от геометрической формы соприкасающихся поверхностей и взаимного расположения их главных нормальных сечений. В технических устройствах наиболее часто имеет место контакт тел, ограниченных поверхностями вращения. При этом оси этих поверхностей могут располагаться параллельно или накрест друг другу, а сами поверхности находиться при внешнем или внутреннем соприкасании.
В работе [1] приведены формулы для величин 1/R1, 1/R2 в зависимости от конкретных условий соприкасания тел, вычисление значений R1 и R2 по которым не вызывает каких-либо затруднений. Однако определение геометрических параметров области контакта сопряжено со значительными затруднениями, обусловленными нахождением решения уравнения (1) и вычислением значений интегралов (2), подынтегральные функции которых не имеют первообразных. При этом приходится одновременно решать две взаимосвязанные задачи вычислительной математики – задачу нахождения корня нелинейного уравнения (1) и численного решения интегралов (2).
В отдельных случаях можно избежать необходимость решения вышеуказанных математических задач, используя таблицу [1], в которой для отдельных значений отношения R2/R1 приведены соответствующие значения эксцентриситета e и значение коэффициента αa формулы (3) для полуоси a площадки контакта. Однако при решении практических задач далеко не всегда в таблице имеется информация о значениях e и αa для полученного в задаче отношения R2/R1. Кроме того, возможна ситуация отсутствия самой таблицы. Вместе с тем проблема поиска величин e и αa значительно упрощается при наличии интерполяционных многочленов, аппроксимирующих аналитическую зависимость e и αa от величины отношения R2/R1.
Постановка задачи. В приведенной ниже таблице приведены значения отношения R2/R1 и коэффициента αa для значений эксцентриситета e2, наиболее часто используемых в технических задачах.
Построить интерполяционные многочлены, описывающие зависимости величин R2/R1 и αa от эксцентриситета e2.
Таблица
| e2 | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| R2/R1 | 1 | 0,925 | 0,846 | 0,765 | 0,682 | 0,594 | 0,502 | 0,405 | 0,297 |
| αa | 0,722 | 0,731 | 0,741 | 0,753 | 0,767 | 0,783 | 0,803 | 0,829 | 0,863 |
Задание
1. Выбрать вид интерполяционного многочлена, описывающие зависимости величин R2/R1 и αa от эксцентриситета e2. Привести обоснование выбора многочлена.
2. Выполнить постановку вычислительной задачи. Разработать алгоритм реализации численного метода на ЭВМ.
3. Вычислить коэффициенты выбранного вида многочленов для функций R2/R1 и αa и произвести проверку работоспособности полученных многочленов.
4. Произвести оценку погрешностей полученных многочленов.
Литература
1. Лурье А.И. Теория упругости. М.: Наука, 1970. – 940с.
Тема № 10
Задача построения эмпирической зависимости высоты неровностей
от подачи при точении стальных заготовок
Содержательная постановка задачи. Одной из основных задач экспериментальных исследований является задача нахождение связей между параметрами и факторами процессов и явлений, лежащих в основе их развития, и описание этих связей в математической форме. Постановка таких задач обычно имеет следующий вид.
Выполнен эксперимент по исследованию влияния подачи s на величину неровностей Rz при точении стали 4Х10С2М, результаты которого приведены в табл. 1.
Таблица 1
Дата добавления: 2019-01-14; просмотров: 183; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
