Методы фазового пространства.

⇐ ПредыдущаяСтр 3 из 3

Предположим, что нелинейная система управления описывается системой обыкновенных дифференциальных уравнений с постоянными коэффициентами.

(1)

Системы такого вида называют динамическими системами. Название это заимствовано из механики.

Предположим, что функции F_k и их производные по всем переменным х_j непрерывны.

Используя векторную запись, условимся обозначать:

(2)

Система (1) можно кратко записать:

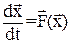(3)

Решение системы:

Вектор начальных условий:

Решение системы (1) однозначно определяется вектором начальных условий, заданных в некоторый момент времени t = t₀. (Обычно t₀ = 0).

Поэтому более наглядной является обозначение: (4)

Или короче:

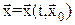(5)

Замечание.

Сформулированные ограничения на функции F_k являются часто слишком жёсткими для систем автоматического управления. Во многих случаях необходимо рассматривать функции F_k , являющиеся кусочно-линейными, разрывными и даже неоднозначными.

Тем не менее, целесообразно начать изучение системы (1) с вышеприведенных, общепринятых в математике классических ограничений для функции F_k, так только в этом случае разработана общая теория.

Рассмотрим некоторые фундаментальные понятия в общем виде, затем перейдем к изучению нелинейных систем второго порядка вида (6)

Отметим, что фактически изучение нелинейных систем мы начнём со случая системы второго порядка:

(6)

Пространство переменных х₁, х₂, …, х_n назовем фазовым пространством, а сами эти переменные – фазовыми переменными или фазовыми координатами.

В теории управления последние годы несколько изменилась терминология, и фазовое пространство называют пространством состояния системы (1) соответственно х₁, х₂, …, х_n – переменными в пространстве состояния. Однако в данной работе мы будем придерживаться «фазовой» терминологии.

Пусть функции х₁(t), х₂(t), …, х_n(t) являются решениями системы (1) при изменении t от 0 до ∞. Для фиксированного момента времени t мы получаем набор чисел, определяющих точку в фазовом пространстве. Если рассматриваем процесс при изменении t, то эту точку будем называть изображающей точкой, а линию, которую она прочерчивает в пространстве при изменении t от 0 до ∞, условимся называть фазовой траекторией.

Иначе можно сказать, что каждое решение системы (1) определяет линию в фазовом пространстве, а если все постоянные, то оно определяет точку. Эту точку называют «положение равновесия» или «особая точка». Линию, определяемую решением уравнения (1), называют фазовой траекторией. Это же название используется для случая, когда решением является точка. То есть мы получаем траекторию-точку.

Свойства фазовых траекторий.

1. Решения и определяют одну и ту же траекторию. Иными словами сдвиг решения по времени не изменяет фазовую траекторию системы (1).

2. Любые две фазовые траектории или не имеют общих точек или совпадают, то есть фазовая траектория не может иметь самопересечений, и две различные фазовые траектории не могут пересекаться.

3. Даже если решение с увеличением t неограниченно приближается к точке покоя , изображающая точка не может прийти в точку за конечное время.

4. Если - периодическое решение системы (1), то ему соответствует замкнутая фазовая траектория. (без самопересечений).

5. Каждая фазовая траектория является или

а) незамкнутой линией без самопересечений;

b) замкнутой линией без самопересечений ;

с) точкой.

Важнейшим вопросом при изучении динамических систем является определение и исследование стационарных (установившихся) движений.

Отметим, что термин движения для обозначения решения системы уравнений (1) заимствован из механики и получил широкое распространение.

а) Наиболее важный тип стационарных движений – это состояния равновесия, которые определяются системой конечных уравнений, получаемых из системы (1), когда производные равны нулю.

(7)

b ) Вторым по важности классом стационарных движений в динамической системе являются периодические движения, то есть такие движения, в процессе которых фазовые переменные совершают колебания с периодом Т:

(10)

Как уже отмечалось траектория, соответствующая периодическим движениям, является замкнутой кривой в фазовом пространстве.

Необходимо различать два принципиально разных вида периодических движений. Это предельные циклы и консервативные движения.

Предельный цикл представляет собой изолированную замкнутую траекторию. В достаточно малой окрестности этой траектории не существует других замкнутых траекторий. Все траектории в этой окрестности или «наматываются» на предельный цикл, либо удаляются от него. (Подробнее этот вопрос будет разъяснен дальше)

Очень важное явление в технике – автоколебания. Автоколебаниям соответствуют в фазовом пространстве устойчивые (понятие устойчивости будет разъяснено дальше) предельные циклы.

Консервативные движения в технических системах встречаются исключительно редко.

c ) Третьим видом стационарных движений являются квазипериодические движения. Их еще называют ограниченными непериодическими движениями. Этот вид стационарных движений очень редко встречается в технических системах.

Введем понятие устойчивость по Ляпунову положения равновесия. Сначала опишем идею, потом приведем формулировку.

В 1892 году один из наиболее крупных русских математиков А.М.Ляпунов опубликовал классическую работу «Общая задача об устойчивости движения». В этой работе он предложил два метода исследования устойчивости положения равновесия.

Положение равновесия называется устойчивым по Ляпунову, если оно удовлетворяет следующему условию. Пусть начальные условия решения системы (1) достаточно близки к положению равновесия . В этом случае решение системы будет оставаться близким к точке покоя для всех t > 0.

Ляпунов доказал следующую теорему.

1. Все корни характеристического уравнения находятся в левой полуплоскости (имеют отрицательную действительную часть). В этом случае положение равновесия асимптотически устойчиво.

2. Хотя бы один корень характеристического уравнения находится в правой полуплоскости (имеет положительную действительную часть). В этом случае положение равновесия неустойчиво.

3. В правой полуплоскости нет корней характеристического уравнения, но на мнимой оси есть один или несколько корней (остальные находятся в левой полуплоскости). Этот случай Ляпунов назвал критическим. Для суждения об устойчивости использовать линеаризованную систему (10) нельзя. Необходимо использовать нелинейные члены при разложении функции F_k в ряд.

Впервые применил метод функции Ляпунова для исследования систем автоматического управления ленинградский ученый А.И.Лурье в конце 40-х годов. В 1951 году вышла его книга, которая была переведена на английский язык и положила начало большому числу исследований в СССР, США и других странах.

Рассмотрим типы фазовых траекторий для линейного уравнения второго порядка.

(13)

Уравнению (13) соответствует система двух уравнений:

(14)

Система (14), очевидно, имеет единственную особую точку (точку покоя) – (0,0). Устойчивость этой особой точки целиком определяется корнями характеристического уравнения. От корней характеристического уравнения системы (14) зависит форма фазовых траекторий. Особой точке в зависимости от корней характеристического уравнения присваивается имя собственное:

1. два действительных отрицательных корня – устойчивый узел.

2. два действительных положительных корня – неустойчивый узел.

3. два комплексных корня в левой полуплоскости – устойчивый фокус.

4. два комплексных корня в правой полуплоскости – неустойчивый фокус.

5. два мнимых корня – центр.

6. два действительных корня. Один - положительный, другой – отрицательный – седло.

Рис. 7

Фазовый портрет для особой точки типа центр представляет собой простейший пример бесконечного семейства консервативных движений.

Фазовый портрет для особой точки типа центр имеет вид, показанный на рисунке 8.

Рис. 8

__________________________________________

По материалам учебника: Лозинский Л.Д. Учебное пособие по курсу ТАУ "Нелинейные системы". (Более подробно см. оригинал)

Дата добавления: 2019-01-14; просмотров: 438; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!