Нелинейные характеристики, содержащие люфт.

Тема 9. Нелинейные системы автоматического управления

 

Типовые нелинейные звенья. Фазовое пространство и фазовая плоскость. Изображение переходных процессов на фазовой плоскости. Устойчивость нелинейных систем по Ляпунову. Исследование устойчивости методом гармонической линеаризации. Дискретные нелинейные системы. Влияние нелинейностей кинематических передач станка на режим работы электропривода. Анализ нелинейных систем автоматического управления асимптотическими методами. Понятие об автоколебаниях динамической системы станка.

 

Система автоматического управления называется нелинейной, если она включает один или несколько нелинейных блоков.

Блок является нелинейным, если зависимость между его выходом и входом описывается или нелинейной функцией (статический блок), или нелинейным дифференциальным или интегральным уравнением (динамический блок).

Практика применения систем авторегулирования еще в конце 19-го века показала, что во многих системах авторегулирования имеют место принципиально иные явления, то есть описание с помощью линейной модели для них неприменимо. На первое место по распространенности и важности среди этих явлений необходимо выделить следующее.

При начальных отклонениях, выше некоторого определенного порога (для каждой системы своего), возникают колебания, определенной амплитуды и частоты. Эти колебания, которые называют автоколебаниями, отличаются тем, что их параметры не зависят от начальных условий, если эти начальные условия находятся в определенной области. Иными словами, в том случае, когда начальные условия процесса в нелинейной системе находятся в указанной области, то возникающий процесс со временем практически сливается с процессом автоколебаний. Можно сказать, что автоколебания как бы обладают областью притяжения. В общем случае в нелинейной системе возможны несколько видов автоколебаний, каждое из которых обладает своей областью притяжения. Области эти между собой не пересекаются.

Еще одно очень опасное явление часто встречается в нелинейных системах. Система устойчиво работает до тех пор, пока отклонения ее координат (или возмущающие воздействия) не превысят определенного порога. Как только они превышают этот порог (для каждой системы свой), возникают расходящиеся процессы. То есть выходной сигнал системы колебательным или монотонным образом начинает неограниченно возрастать, что, разумеется, приводит к катастрофе, если не принять специальных мер.

В нелинейной системе возможна ситуация, когда один вид движения устойчив, а другой неустойчив. Здесь мы под словом «устойчив» понимаем «прочность движения» по отношению к изменению начальных условий

При исследовании динамики нелинейных систем требуется определить условия, при которых нелинейная система как бы подобна линейной системе. (Она имеет единственное положение равновесия и приходит к нему при любых начальных отклонениях ее координат. Такой класс систем называется абсолютно устойчивыми системами.) и найти условия, при которых в системе имеют место автоколебания. (Выяснить, какова область их притяжения. Сразу же отметим, что в общем случае это очень трудная задача. Однако, для многих практически важных случаев разработаны методы ее точного или приближенного решения).

Для изучения этих систем найдены простые методы, которые позволяют результаты, полученные для систем второго порядкаприменить к исследованию процессов в нелинейных системах высокого порядка.

Рассмотрим типовые нелинейные блоки систем автоматического управления, то есть нелинейные функции, которые наиболее часто встречаются в промышленных системах автоматического управления.

В системах управления встречаются нелинейные элементы, имеющие самые различные статические характеристики. Однако, можно выделить некоторое число статических характеристик, которые, во-первых, встречаются чаще других, и, во-вторых, могут быть с достаточной степенью точности аппроксимированы кусочно-линейными функциями Эти характеристики получили название типовых. Ниже приводится таблица графиков типовых статических характеристик и их математического описания.

Однозначные нелинейности

Статическая характеристика. 

Математическое описание в форме u = N ( x )                   .

НЭ1 Рис.1 Н.э. – ограничение (насыщение)		Если |x|<a то u= k·x если |x|>a то u=c·sign(x)
НЭ2 Рис. 2 Н.э. – переменный коэф. усиления (2 значения )		Если |x|<a то u= k1·x если |x|>a то u= k2·x-a·(k2 - k1)·sign(x)
НЭ3 рис. 3 н.э. – переменный коэф. усиления (3 значения)		Если |x|≤ b1 то u= k1·x если b1<|x|< b2 то u= k2·x + B2·sign(x) если |x|≥ b2 то u=k3·x + B3·sign(x) где B2=b1·(k1-k2) B3=b1·( k1-k2) + (k2-k3)·b2
НЭ4 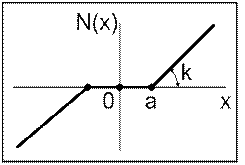Рис.4 Н.э. –нечувствительность	если |x|≤a то u=0 если |x|>a то u=k·x - k·a·sign(x)
НЭ5 Рис. 5 Н.э. – нечувствительность и ограничение	Если |x|≤a то u=0 если a<|x|<b то u= k·x - k·a·sign(x) если |x|>b то u=c ·sign(x)
НЭ6 Рис. 6 Н.э. – нечувствительность и переменный коэф. усиления	Если |x|≤a то u=0 если a<|x|<b то u= k1·x + B1·sign(x) если |x|>b то u=k2·x + B2·sign(x) B1=-k1·a B2=(k1-k2) ·b – k1·a
НЭ7 Рис. 7 Н.э. – двухпозиционное реле	u=c·sign(x)

 

 

НЭ8 Рис. 8 Н.э. – трёхпозиционное реле

Если |x| ≤a то u=0 если |x|>a то u=c ·sign(x)

 

Неоднозначные нелинейности

Реле с обычным гистерезисом

            Математическое описание в форме

Статическая характеристика                            u_n = N(x_n ,u_n-1)

 Индекс «n» соответствует текущему значению сигнала, индекс «n-1» - предшествующему значению, n=1,2,3…

 

НЭ9 Рис. 9 Н.э. – двухпозиционное реле с гистерезисом (положительным)	если | xn |>a то un = sign(xn) если | xn |<a то un = un-1 при значении входного сигнала |x|=а, выходной сигнал скачком изменяет значение с «с» на «-с»
НЭ10 Рис. 10 Н.э. – трёхпозиционное реле с гистерезисом (положительное)	если |xn |<a то un =0 если a<|xn |<b то un = un-1   если |xn |>b то un = с·sign(xn) при значении входного сигнала |x|=а или |x|=b, выходной сигнал скачком изменяет своё значение, как показано на рисунке10

Реле с опережением

Статическая характеристика.            Математическое описание в форме

                                           u=N(x_n, x_n-1, u_n-1)

НЭ11 Рис. 11 Н.э. – двухпозиционное реле с отрицательным гистерезисом (с опережением)	если | xn|>a то un=c ·sign(xn) если | xn|<a и | xn-1|>a то un=- un-1   если | xn|<a и | xn-1|<a  то un= un-1   при значении входного сигнала |x|=а, выходной сигнал скачком изменяет значение, причём изменение может происходить в двух направлениях, как показано на рисунке11.
НЭ12 Рис. 12 Н.э. – трёхпозиционное реле с отрицательным гистерезисом (с опережением)	если |xn |>b то un =c ·sign(xn) если | xn|<a то un=0 если a<| xn|<b и a<| xn-1|<b то un = un-1 если a<| xn|<b и | xn-1|<a то un =c·sign(xn) если a<| xn|<b и | xn-1|<b то un =0

 

Нелинейные характеристики, содержащие люфт.

Статическая характеристика.            Математическое описание в форме

                                           u=N(x_n, x_n-1, u_n-1)

НЭ13 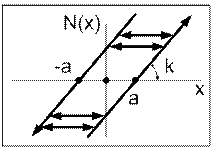Рис. 13 Н.э. - люфт	Вычисляем значения xα и xβ (см. рис. 13а) xα = -a + un-1 /k xβ = a + un-1 /k Если |xα|< |xn|< |xβ| то un= un-1 если |xn|< |xα| то un = k · (xn +a) если |xn|> |xβ| то un = k · (xn +a)
Рис. 13а (вспомогательный)
НЭ14 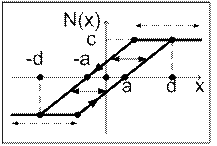Рис. 14 Н.э. – люфт, ограничение	Вычисляем k=c/(d - a) Если |xn|>d то un=c ·sign(xn) если | xn|<d то описание совпадает с нелинейностью люфт

 

---

Дата добавления: 2019-01-14; просмотров: 587; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!