Интегрирование тригонометрических функций
Интегралы вида  в общем случае вычисляются подстановкой
в общем случае вычисляются подстановкой  (универсальная подстановка).
(универсальная подстановка).
При этом  ,
,  ,
, 
и подынтегральная функция становится рациональной функцией от  .
.
Задача 23. Найти  .
.
Решение.
Делая подстановку  и используя соответствующие формулы для
и используя соответствующие формулы для  , интеграл запишем в виде:
, интеграл запишем в виде: 

Ответ.  .
.
Задача 24. Найти  .
.
Решение. Выполним универсальную подстановку  .
.
Тогда, используя указанные формулы для  , получаем:
, получаем:


= 
 =
=  .
.
Ответ.  .
.
!Интегралы вида  , где
, где  - целые числа, удобно вычислять подстановкой
- целые числа, удобно вычислять подстановкой  .
.
!Интегралы вида  , где
, где  - числа разной четности, вычисляются подстановкой
- числа разной четности, вычисляются подстановкой  , если
, если  четно и
четно и  , если
, если  четно.
четно.
!Интегралы вида  ;
; 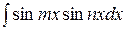 ;
;  , где
, где  , вычисляются с использованием формул тригонометрии, преобразующих произведение тригонометрических функций в их сумму:
, вычисляются с использованием формул тригонометрии, преобразующих произведение тригонометрических функций в их сумму:


 .
.
Задача 25. Найти  .
.
Решение. В подынтегральную функцию входит четная степень  , поэтому вводим новую переменную
, поэтому вводим новую переменную 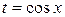 , тогда
, тогда  . Выполним следующие преобразования:
. Выполним следующие преобразования:



 .
.
Ответ. 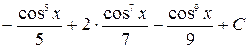 .
.
Задача 26. Найти  .
.
Решение. Воспользуемся формулой произведения синусов:
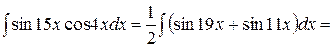
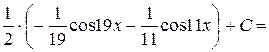
 .
.
Ответ.  .
.
Интегрирование иррациональных выражений
После соответствующей замены переменных многие иррациональные функции можно свести либо к рациональным дробям, либо к тригонометрическим выражениям, интегрирование которых будет рассмотрено ниже.
Для дробно-линейных иррациональностей удобной заменой является выбор в качестве новой переменной подкоренного выражения в степени  , где р – наименьший общий знаменатель дробных степеней в подынтегральном выражении.
, где р – наименьший общий знаменатель дробных степеней в подынтегральном выражении.
|
|
|
Задача 27. Найти  .
.
Решение. Сделаем замену переменной:  .
.
Тогда  ,
,  Подставим полученные результаты в подынтегральное выражение:
Подставим полученные результаты в подынтегральное выражение:




Ответ. 
При интегрировании квадратичных иррациональностей привести подынтегральное выражение к рациональному виду помогают тригонометрические замены:
 , если в подынтегральную функцию входит
, если в подынтегральную функцию входит  ,
,
 для
для  ,
,
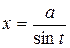 , если подынтегральная функция содержит
, если подынтегральная функция содержит  ,
,  .
.
Задача 28.  .
.
Решение. Выделив полный квадрат в квадратном трехчлене, получим:
 , где u = x + 1. Теперь сделаем замену переменной:
, где u = x + 1. Теперь сделаем замену переменной:  Подынтегральное выражение при этом примет вид:
Подынтегральное выражение при этом примет вид:


Ответ. 
Иногда от квадратичных иррациональностей можно избавиться с помощью замен другого типа.
Задача 29.  .
.
Решение.
Сделаем так называемую обратную подстановку:  ,
,  .
.
Тогда 


Ответ. 
!Интегралы вида  ,
,
где  - целые числа, сводятся к интегралу от рациональных функций заменой переменной
- целые числа, сводятся к интегралу от рациональных функций заменой переменной  , где
, где 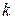 - наименьшее общее кратное чисел
- наименьшее общее кратное чисел  (НОК
(НОК  ). Аналогичная подстановка делается, если вместо
). Аналогичная подстановка делается, если вместо  содержатся выражения вида
содержатся выражения вида  или
или  .
.
|
|
|
Задача 30. Найти  .
.
Решение. Т.к. НОК (2;3)=6, то делаем подстановку:

 ,
,  и исходный интеграл принимает вид:
и исходный интеграл принимает вид:

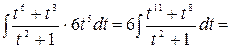



Переходя к переменной  , получим:
, получим:

Ответ. 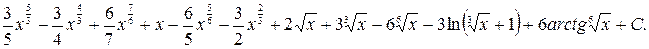 !Интегралы вида
!Интегралы вида  , где
, где  - вещественные числа, в общем случае вычисляются одной из подстановок Эйлера:
- вещественные числа, в общем случае вычисляются одной из подстановок Эйлера:
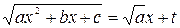 ,
,  ;
;
 ,
,  ;
;
 или
или  ,
,
где  и
и  - различные вещественные корни трехчлена
- различные вещественные корни трехчлена  .
.
Дата добавления: 2019-01-14; просмотров: 145; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
