Интегрирование рациональных дробей.
Методы вычисления интегралов
Непосредственное интегрирование
Задача 1. Найти интеграл
 .
.
Решение. Разбиваем интеграл на три интеграла и работаем с каждым:

Дифференцированием первообразной проверим правильность интегрирования:

Полученное выражение совпадает с подынтегральной функцией, т.е. интегрирование проведено правильно.
Ответ. 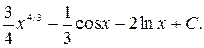
Задача 2.Найти  .
.
Решение. 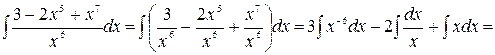
 .
.
Ответ.  .
.
Задача 3 . Найти  .
.
Решение.  .
.
Ответ. 
 .
.
Задача 4.Найти  .
.
Решение. 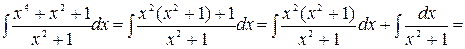
 .
.
Ответ.  .
.
Задача 5 . Найти  .
.
Решение. 
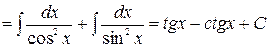 .
.
Ответ.  .
.
Задача 6 . Найти 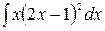 .
.
Решение. 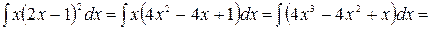
 .
.
Ответ.  .
.
Метод замены переменной (метод подстановки)
Выбор замены определяется видом подынтегральной функции. Цель – выполнить такую замену, в результате которой исходный интеграл превратится в табличный.
За новую переменную иногда выбирают такую функцию, стоящую в подынтегральном выражении, которая содержит под знаком интеграла и свою производную с точностью до постоянного множителя.
Например, удобно обозначать за новую переменную знаменатель дроби подынтегральной функции, если в числителе содержится его производная с точностью до постоянного множителя.
Задача 7.Найти  .
.
Решение. Сделаем замену переменной: x² = t . Тогда  . Следовательно,
. Следовательно, 

Можно было выполнить замену: 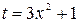 , тогда
, тогда  , а
, а  .
.
Ответ. 
Задача 8 . Найти  .
.
Решение. 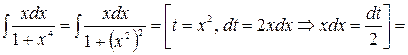

Ответ. 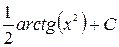 .
.
Задача 9.Найти  .
.
Решение. 
 .
.
Ответ.  .
.
Задача 10. Найти 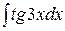 .
.
|
|
|
Решение. 
 .
.
Ответ.  .
.
Часто за новую переменную удобно брать подкоренное выражение, если под знаком интеграла присутствует также его производная с точностью до постоянного множителя.
Задача 11 . Найти  .
.
Решение. 
 .
.
Ответ.  .
.
Задача 12 . Найти 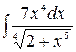 .
.
Решение. 
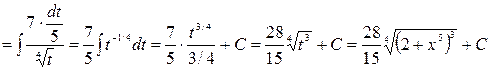 .
.
Ответ.  .
.
За новую переменную иногда выбирают функцию, стоящую в основании степени, если подынтегральное выражение содержит производную этой функции с точностью до постоянного множителя.
Задача 13 . Найти  .
.
Решение. 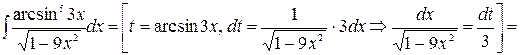
 .
.
Ответ. 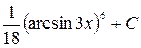 .
.
Задача 14.  .
.
Решение. 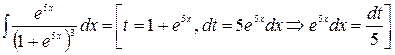 =
=
=  .
.
Ответ.  .
.
Задача 15 . Найти  .
.
Решение.  .
.
Ответ.  .
.
Метод интегрирования по частям.

|
– формула интегрирования по частям.
Задача 16.Найти  .
.
Решение. Обозначим  . Тогда
. Тогда 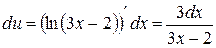 . Далее,
. Далее,  , а потому
, а потому  . Следовательно,
. Следовательно,  . В полученном интеграле выделим целую часть подынтегральной функции (поскольку дробь - неправильная):
. В полученном интеграле выделим целую часть подынтегральной функции (поскольку дробь - неправильная):
 .
.
Окончательно решение выглядит так:

 .
.
Ответ.  .
.
Задача 1 7 . Найти  .
.
Решение. Пусть  ,
,  .
.
Тогда  ;
;  .
.
 =
=  .
.
К последнему интегралу применим метод интегрирования по частям, полагая  ;
;  . Отсюда следует:
. Отсюда следует: 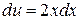 ;
;  , и окончательно получаем:
, и окончательно получаем:
 =
= 
 .
.
Ответ.  .
.
Задача 18 . Найти  .
.
Решение.  =
=
= 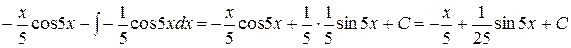 .
.
Ответ.  .
.
Задача 19 . Найти  .
.
Решение.
|
|
|

=  =
=
Чтобы взять последний интеграл, умножим и разделим числитель на 9, затем в числителе прибавим и отнимем единицу, после чего разобьем интеграл на два табличных:
=  =
= 
= 

= 

=  .
.
Ответ.  .
.
Интегрирование выражений, содержащих квадратный трехчлен
Основные идеи заключаются в выделении в квадратном трехчлене полного квадрата и в проведении линейной замены, позволяющей свести исходный интеграл к табличным.
Задача 20. Найти  .
.
Решение. Выделим полный квадрат в знаменателе:  ,
,
тогда 
=  . Применили формулу (14) из таблицы интегралов.
. Применили формулу (14) из таблицы интегралов.
Ответ. 
Задача 21 . Найти  .
.
Решение.
При решении этого примера потребуются дополнительные преобразования, связанные с присутствием переменной в числителе подынтегральной функции. Выделив полный квадрат в знаменателе  , получим:
, получим:
 =
= 
= 
Для второго из интегралов в силу табличной формулы (12) имеем: 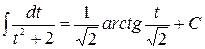 . В первом интеграле проведем внесение под знак дифференциала:
. В первом интеграле проведем внесение под знак дифференциала:
 .
.
Таким образом, собирая все вместе и возвращаясь к переменной x, получаем:

= 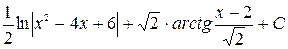 .
.
Ответ.  .
.
Интегрирование рациональных дробей.
Задача 22.Найти  .
.
Решение. Под знаком интеграла стоит рациональная дробь.
1. Так как подынтегральная рациональная дробь неправильная (степень многочлена в числителе выше степени многочлена в знаменателе), то выделим целую часть, разделив числитель на знаменатель “уголком”:
|
|
|





Итак, подынтегральную функцию можно записать в виде:  .
.
Тогда исходный интеграл (обозначим его J), можно представить как сумму интегралов:  .
.
2. Чтобы взять полученный новый интеграл от правильной рациональной дроби (обозначим его J1), разложим знаменатель подынтегральной функции на множители.
Для этого найдем корни квадратного трехчлена, стоящего в знаменателе:
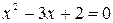
 .
.
Тогда  .
.
3. Представим полученную правильную дробь в виде суммы элементарных дробей:
 (*)
(*)
Здесь А и В - числа, которые нужно найти. В правой части (*) приведем дроби к общему знаменателю 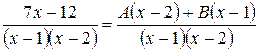 .
.
Так как дроби тождественно равны и равны их знаменатели, то должны быть равны и их числители:
 или
или
 или
или

Это тождество выполняется тогда и только тогда, когда слева и справа равны коэффициенты при одинаковых степенях х. Получаем систему линейных уравнений:

 .
.
Вычитая из второго уравнения первое, получаем  .
.
Тогда  .
.
Подставим найденные числа в равенство (*):
 .
.
4. Вернемся к интегралу J1:
 =
=  =
=  =
=
=  .
.
5. Окончательно искомый интеграл равен:
|
|
|
 .
.
Ответ.  .
.
Дата добавления: 2019-01-14; просмотров: 147; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
