Функция Лапласа и ее свойства
Определение. Функцией Лапласа или интегралом вероятности называется функция вида
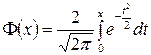
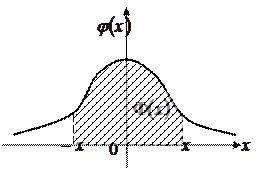
| Графически функция Лапласа представляет площадь под стандартной нормальной кривой на отрезке  .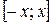
Для значения функции Лапласа составлены специальные таблицы, которые, обычно, приведены во всех учебниках по теории вероятностей.
|
Свойства функции Лапласа
1. 
.
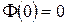2. Функция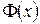 
является нечетной, т.е. 
.
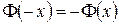3. Функция 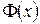монотонно возрастающая, причем при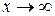 
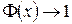
Свойства нормального закона распределения
Теорема. Интегральная функция распределения случайной величины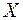 
, распределенной по нормальному закону, имеет вид
.
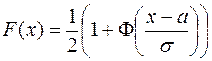Доказательство. Так как интегральная функция распределения по заданной дифференциальной функции определяется по формуле
,
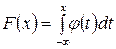то для нормального закона распределения получаем
.
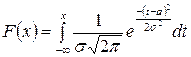Сделав в последнем интеграле замену переменной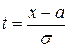 
, получим
.
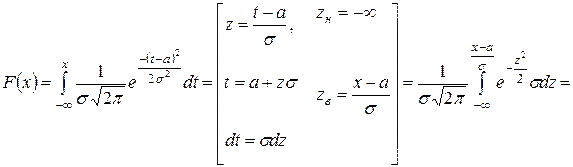
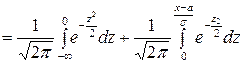С учетом того, что первый интеграл
,
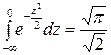а второй интеграл выражается через функцию Лапласа следующим образом
,
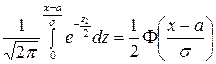окончательно получаем
.
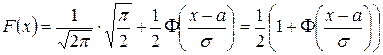С геометрической точки зрения, функция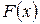 
представляет собой площадь под нормальной кривой на интервале 
.
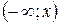Теорема. Вероятность попадания случайной величины 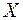, распределенной по нормальному закону, в промежуток 
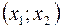определяется по формуле
,
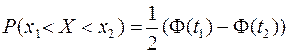где
, 
.
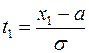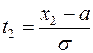Доказательство. Из свойства 5 интегральной функции распределения следует, что вероятность попадания случайной величины на заданный промежуток равна приращению интегральной функции на этом промежутке, т.о.
|
|
|
.
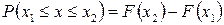Следовательно, для нормального закона
.
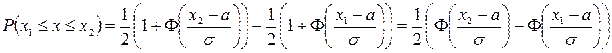Теорема. Если случайная величина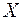 
распределена по нормальному закону, то вероятность того, что случайная величина отклонится от своего математического ожидания по модулю на величину, не превышающую 
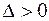, определяется по формуле
,
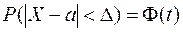где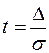 
.
Доказательство. Так как неравенство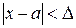 
равносильно двойному неравенству вида
,
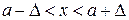то с учетом свойства 2 получим
=
.
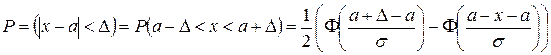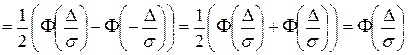Определение. Событие называется практически достоверным, если оно наступает с вероятностью не меньшей 0,9973.
Теорема (правило трех сигма). Если случайная величина 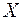распределена по нормальному закону, то вероятность того, что случайная величина отклонится от своего математического ожидания по модулю на величину, не превышающую 
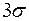, определяется по формуле
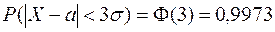
Доказательство. Из свойства 2 следует
.
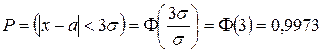Пример. Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина 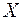с параметрам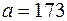и 
и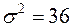 
, найти
1) выражение плотности вероятности и функции распределения случайной величины ;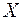
2) доли костюмов четвертого роста (176-182 см.) и третьего роста (170-176 см), которые нужно предусмотреть в общем объеме производства для данной возрастной группы.
|
|
|
Дата добавления: 2018-11-24; просмотров: 2287; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!