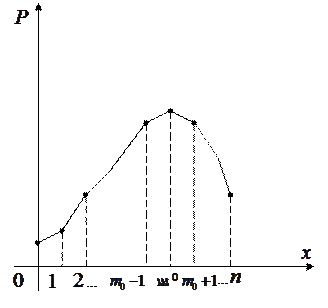Показательное (экспоненциальное) распределение
Законы распределения случайных величин
В этом параграфе мы изучим некоторые конкретные случайные величины, часто используемые в теории вероятностей, математической статистике и их приложениях.
Биномиальное распределение
Случайная величина с биноминальным законом распределения возникает в схеме Бернулли. Пусть проводится серия  независимых испытаний, причем каждое испытание имеет два исхода: «событие
независимых испытаний, причем каждое испытание имеет два исхода: «событие  появилось» или «событие
появилось» или «событие  не появилось». Вероятность появления события
не появилось». Вероятность появления события  в каждом отдельном испытании равна
в каждом отдельном испытании равна  .
.
Определение. Дискретная случайная величина  , возможными значениями которой являются частоты появления события
, возможными значениями которой являются частоты появления события  в
в  независимых испытаниях
независимых испытаниях  , а вероятность соответствующих значений определяются по формуле Бернулли
, а вероятность соответствующих значений определяются по формуле Бернулли

называется биномиальной случайной величиной с параметрами  и
и  .
.
Таким образом, закон распределения биномиальной случайной величины можно записать в виде таблицы 1.
Таблица 1.

| 0 | 1 | … | 
|

| 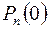
| 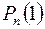
| … | 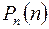
|
Свойства биномиального закона распределения
Свойство 1. Сумма вероятностей всех возможных значений биномиальной случайной величины равна единице, т.е.
 .
.
Доказательство. Так как по определению биномиального закона распределения
 ,
,
то, согласно разложению степени бинома по формуле Ньютона, имеем
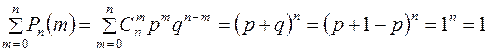 . ●
. ●
Из этого свойства вытекает название биномиального распределения вероятностей.
|
|
|
Свойство 2. Если частота 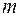 возрастает то нуля до некоторого значения частоты
возрастает то нуля до некоторого значения частоты  , то вероятность соответствующих значений также возрастают до величины
, то вероятность соответствующих значений также возрастают до величины  , а при дальнейшем возрастании частоты
, а при дальнейшем возрастании частоты 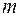 вероятности соответствующих значений убывают.
вероятности соответствующих значений убывают.
Доказательство. Выведем условия, при которых вероятности 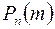 с ростом
с ростом 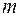 возрастают, т.е. удовлетворяют неравенству
возрастают, т.е. удовлетворяют неравенству
 или
или  . (1)
. (1)
Так как
 ;
;  ,
,
то из равенства (1) получаем
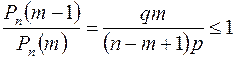 ,
,
откуда находим

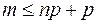 (2)
(2)
Следовательно, при возрастании 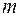 от нуля до
от нуля до  вероятности соответствующих значений монотонно возрастают.
вероятности соответствующих значений монотонно возрастают.
Аналогично выводим условие, при котором вероятности соответствующих значений 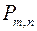 с ростом
с ростом 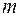 убывают.
убывают.
Если
 ,
,
то
 . (3)
. (3)
Так как
 ,
,
то
 ,
,
откуда находим

 . (4)
. (4)
Следовательно, при возрастании 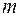 от
от  до
до  вероятности соответствующих значений монотонно убывают.
вероятности соответствующих значений монотонно убывают.
Таким образом, существует частота, которой соответствует наибольшая вероятность.
Определение. Частота, которой соответствует наибольшая вероятность при заданных параметрах  и
и  называется наивероятнейшей частотой.
называется наивероятнейшей частотой.
Наивероятнейшую частоту обычно обозначают  .
.
|
|
|
Свойство 3. Наивероятнейшая частота определяется из двойного неравенства
 .
.
Доказательство. Из определения наивероятнейшей частоты получаем
 и
и  .
.
Согласно свойству 2, имеем
 ; (5)
; (5)
 . (6)
. (6)
Объединив неравенства (5) и (6) получаем двойное неравенство для определения наивероятнейшей частоты 
 .
.
Если  целое число, то наивероятнейшая частота принимает два значения:
целое число, то наивероятнейшая частота принимает два значения:
 или
или 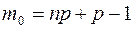 .
.
Если  дробное число, то наивероятнейшая частота имеет единственное значение, которое равно целой части числа
дробное число, то наивероятнейшая частота имеет единственное значение, которое равно целой части числа  , т.е.
, т.е.
 .
.
Из рассмотренных свойств биномиального закона распределения следует, что полигон распределения вероятностей биномиальной случайной величины имеет вид
|
 целое число целое число
|
Свойство 4. Числовые характеристики биноминальной случайной величины вычисляются по формулам
 ,
,  ,
,  .
.
Доказательство. Математическое  можно найти, пользуясь определением математического ожидания случайной величины, что приводит к громоздким вычислениям.
можно найти, пользуясь определением математического ожидания случайной величины, что приводит к громоздким вычислениям.
Более простой путь состоит в следующем. Свяжем с  ым испытанием случайную величину
ым испытанием случайную величину  , которая сможет принимать только два значения:
, которая сможет принимать только два значения:
|
|
|
 , если в
, если в  ом испытании событие
ом испытании событие  произошло, вероятность этого значения
произошло, вероятность этого значения  ;
;
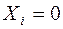 , если в
, если в  ом испытание событие
ом испытание событие  не произошло,
не произошло, 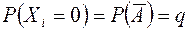 .
.
Так как испытания в схеме Бернулли независимы, то независимы случайные величины  , причем закон распределения каждой из них имеет вид
, причем закон распределения каждой из них имеет вид

| 0 | 1 |
|

| 
| 
|
Найдем математическое ожидание случайной величины 


Найдем теперь дисперсию
 .
.
Очевидно, частота 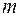 наступления события
наступления события  в
в  независимых испытаниях равна сумме рассматриваемых случайных величин
независимых испытаниях равна сумме рассматриваемых случайных величин  .
.
 .
.
Пользуясь свойством 4 математических ожиданий, получаем

Пользуясь свойством 4 дисперсии, находим
 .
.
По определению среднего квадратического отклонения
 .
.
Итак, доказано, что числовые характеристики частоты вычисляются по формулам:
 , (7)
, (7)
 , (8)
, (8)
 . (9)
. (9)
Следствие. Числовые характеристики относительной частоты  вычисляются по формулам:
вычисляются по формулам:
 ,
,  ,
,  .
.
Доказательство. Воспользовавшись формулой 7 и свойством 2 математического ожидания, получаем
|
|
|
 .
.
Из формулы 8 и второго свойства дисперсии, следует
 .
.
Согласно определению среднего квадратического отклонения случайной величины, получаем
 . ●
. ●
Пуассоновское распределение
Если число испытаний  увеличивается, то увеличивается число членов биномиального распределения. Так как сумма вероятностей всех возможных значений остается равной единице, то значение вероятности каждого отдельного значения уменьшается. Этим объясняется то, что закон Пуассона иногда называют законом резких событий.
увеличивается, то увеличивается число членов биномиального распределения. Так как сумма вероятностей всех возможных значений остается равной единице, то значение вероятности каждого отдельного значения уменьшается. Этим объясняется то, что закон Пуассона иногда называют законом резких событий.
Определение. Дискретная случайная величина  , возможными значениями которой являются
, возможными значениями которой являются  , а вероятности соответствующих значений определяются по формуле Пуассона
, а вероятности соответствующих значений определяются по формуле Пуассона
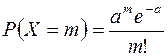
называется пуассоновской случайной величиной с параметром  .
.
Пуассоновское распределение широко используется в теории массового обслуживания. Число  называется интенсивностью.
называется интенсивностью.
Закон распределения Пуассоновской случайной величины можно записать в виде таблицы 2:
Таблица 2.
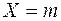
| 1 | 2 | … | 
| |

| 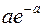
| 
| … | 
| … |
Свойства закона распределения Пуассона.
Свойство 1. Сумма вероятностей всех возможных значений пуассоновской случайной величины равна единице, т.е.
 .
.
Доказательство. Найдем сумму ряда
 . ●
. ●
Свойство 2. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны между собой, причем имеют место равенства
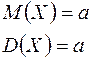 .
.
Доказательство. Пользуясь определением математического ожидания, находим математическое ожидание пуассоновской случайной величины, заданной таблицей 2.
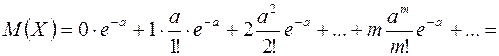
 .
.
Итак, доказано, что
 .
.
Найдем теперь дисперсию пуассоновской случайной величины
 .
.
Вычислим  , получим
, получим



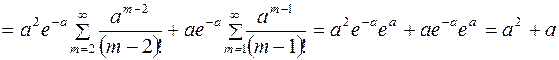 .
.
Поэтому
 . ●
. ●
Равномерное распределение
Определение. Непрерывная случайная величина называется равномерно распределенной на отрезке  , если плотность распределения вероятности постоянна на отрезке
, если плотность распределения вероятности постоянна на отрезке  и равна нулю вне его.
и равна нулю вне его.
Из определения следует, что дифференциальная функция равномерно распределенной случайной величины имеет вид

Свойства равномерного распределения
Свойство 1. Дифференциальная функция равномерно распределенной на отрезке  случайной величины записывается в виде
случайной величины записывается в виде
 (1)
(1)
Доказательство. Найдем постоянную  , воспользовавшись свойством 4 дифференциальной функции распределения
, воспользовавшись свойством 4 дифференциальной функции распределения
 .
.
Откуда получаем
 .
.
Следовательно, плотность вероятностиравномерно распределенной случайной величины имеет вид

График плотности вероятности  равномерно распределенной случайной величины изображен на рисунке 1.
равномерно распределенной случайной величины изображен на рисунке 1.
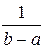
|



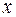
Рис. 1.
Свойство 2. Интегральная функция распределения случайной величины, равномерно распределенной на отрезке  , записывается в виде
, записывается в виде
 .
.
Доказательство. Для того, что бы найти интегральную функцию распределения равномерно распределенной случайной величины воспользуемся свойством 3 дифференциальной функции распределения
 .
.
Рассмотрим следующие три случая
| 1) Если  , то , то  при при  .
Поэтому .
Поэтому  . .
| |||
      
 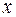  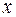
| 2) Если  , то из свойства аддитивности определенного интеграла получаем , то из свойства аддитивности определенного интеграла получаем   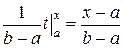 . .
| |||
      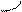  
  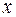 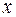
| 3) Если  , то, воспользовавшись свойством аддитивности определенного интеграла, находим , то, воспользовавшись свойством аддитивности определенного интеграла, находим
|



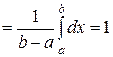 .
.
Объединив рассмотренные три случая, находим

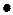
График интегральной функции  равномерно распределенной случайной
равномерно распределенной случайной
величины изображен на рисунке 2
|
Рис. 2.
Свойство 3. Математическое ожидание случайной величины, равномерно распределенной на отрезке  , определяется по формуле
, определяется по формуле
 .
.
Доказательство. Вычислим математическое ожидание равномерно распределенной случайной величины, воспользовавшись формулой
 .
.
Откуда с учетом (1) получаем

 .
.
Свойство 4. Дисперсия случайной величины, равномерно распределенной на отрезке  , определяется по формуле
, определяется по формуле
 .
.
Доказательство. Воспользовавшись формулой для вычисления дисперсии непрерывной случайной величины
 ,
,
для равномерно распределенной случайной величины находим


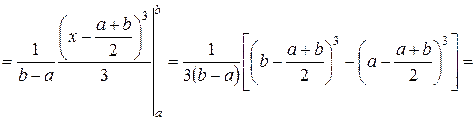
 . ●
. ●
Свойство 5. Среднее квадратическое отклонение случайной величины равномерно распределенной на отрезке  , вычисляется по формуле
, вычисляется по формуле
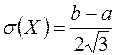 .
.
Доказательство. Так как среднее квадратическое отклонение

 ,
,
то среднее квадратическое отклонение для равномерно распределенной случайной величины находим
 . ●
. ●
Пример 1. Случайная величина равномерно распределена на интервале  . Найти: а) дифференциальную функцию распределения и построить ее график;
. Найти: а) дифференциальную функцию распределения и построить ее график;
б) интегральную функцию распределения и построить ее график;
в) числовые характеристики заданной случайной величины.
Показательное (экспоненциальное) распределение
Определение. Непрерывная случайная величина  , плотность распределения которой задается формулой
, плотность распределения которой задается формулой

называется показательной или экспоненциальной с параметром 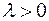 .
.
График плотности вероятности 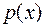 равномерно распределенной случайной величины изображен на рисунке 1
равномерно распределенной случайной величины изображен на рисунке 1

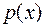





Рис. 1.
В большом числе случаев показательное распределение описывает время безотказной работы прибора, при этом число  интерпретируется как интенсивность отказа. Это распределение находит также широкое применение в демографии.
интерпретируется как интенсивность отказа. Это распределение находит также широкое применение в демографии.
Свойства показательного распределения
Свойство 1. Интегральная функция распределения показательной случайной величины записывается в виде
 .
.
Доказательство. Для того, что бы найти интегральную функцию распределения показательной случайной величины, воспользуемся свойством 3 дифференциальной функции распределения
 .
.
Рассмотрим следующие два случая:
1) Если  , то
, то  при
при  . Поэтому
. Поэтому
 .
.
2) Если  , то из свойства аддитивности определенного интеграла получаем
, то из свойства аддитивности определенного интеграла получаем




 .
.
Из рассмотренных случаев следует, что интегральная функции  показательно распределенной случайной величины записывается в виде
показательно распределенной случайной величины записывается в виде


График интегральной функции  показательно распределенной случайной величины изображен на рисунке 2
показательно распределенной случайной величины изображен на рисунке 2
     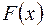
|
Рис. 2.
Свойство 2. Математическое ожидание случайной показательной случайной величины определяется по формуле
 .
.
Доказательство. Вычислим математическое ожидание равномерно распределенной случайной величины, воспользовавшись формулой
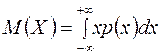 .
.
Откуда с учетом (1) получаем

 .
.
Свойство 3. Дисперсия случайной величины показательной случайной величины определяется по формуле
 .
.
Доказательство. Воспользовавшись формулой для вычисления дисперсии непрерывной случайной величины
 ,
,
для равномерно распределенной случайной величины находим


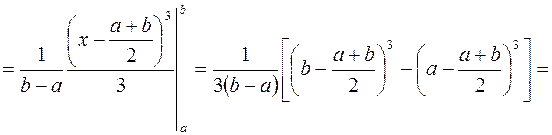
 . ●
. ●
Свойство 4. Среднее квадратическое отклонение случайной величины показательной случайной величины вычисляется по формуле
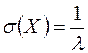 .
.
Доказательство. Так как среднее квадратическое отклонение

 ,
,
то среднее квадратическое отклонение для равномерно распределенной случайной величины находим
 . ●
. ●
Пример 1. Случайная величина равномерно распределена на интервале  .
.
Найти: а) дифференциальную функцию распределения и построить ее график;
б) интегральную функцию распределения и построить ее график;
в) числовые характеристики заданной случайной величины.
Дата добавления: 2018-11-24; просмотров: 656; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!