Приведение уравнения второго порядка к каноническому виду.
Определение 3.4.4.1. Линия, определяемая общим уравнением второго порядка
 , (3.41)
, (3.41)
называется алгебраической линией второго порядка.
Для квадратичной формы  можно задать матрицу
можно задать матрицу
 . (3.42)
. (3.42)
Для того чтобы перейти к новой системе координат, в которой уравнение линии будет иметь канонический вид, необходимо провести два преобразования:
1) поворот координатных осей на такой угол, чтобы их направление совпало с направлением осей симметрии кривой (если она имеет две оси);
2) параллельный перенос, при котором начало координат совмещается с центром симметрии кривой (если он существует).
Замечание. Для параболы новые оси координат должны располагаться параллельно и перпендикулярно директрисе, а начало координат – совпасть с вершиной параболы.
Параллельный перенос.
Пусть задана система координат (О, е1, е2, е3) и точка О′(a, b, c). Требуется параллельным переносом перенести систему координат в О’. При этом новый базис обозначим 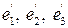 , старые координаты точки А - х, y, z, а новые x′, y′, z′ (рис. 3.14).
, старые координаты точки А - х, y, z, а новые x′, y′, z′ (рис. 3.14).

Рис.3.14. Параллельный перенос
Координаты векторов  (a, b, c), вектора
(a, b, c), вектора 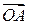 (x, y, z),
(x, y, z),  (x′, y′, z′). И
(x′, y′, z′). И  =
=  +
+  или
или 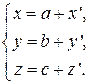 Таким образом формулы параллельного переноса
Таким образом формулы параллельного переноса
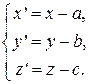 (3.43)
(3.43)
|
|
|
Поворот системы координат (рис 3.15).

Рис. 3.15. Поворот на плоскости
Координаты новых базисных векторов i’(cosj, sinj), j’(–sinj, cosj). По формулам перехода к новому базису от старого раздела 2.9.3 получаем 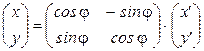 или
или  (3.44)
(3.44)
Упрощение уравнений второго порядка.
Сначала осуществим поворот на угол j для того, чтобы избавиться от смешанного произведения переменных. Подставим в уравнение (3.41) формулы (3.44). После простых преобразований получаем, что коэффициент при x′, y′ равен  . Приравниваем его к 0, из чего получаем следующее соотношение, позволяющее определить угол j:
. Приравниваем его к 0, из чего получаем следующее соотношение, позволяющее определить угол j:
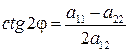 (3.45)
(3.45)
Таким образом, нам удалось определить требуемый угол поворота. Исходное уравнение принимает вид
 (3.46)
(3.46)
1) Если  , то после выделения полного квадрата по каждой из переменных получаем
, то после выделения полного квадрата по каждой из переменных получаем

Осуществим параллельный перенос:

тогда исходное уравнение принимает вид
 (3.47)
(3.47)
2) Если  ,
,  ,
,  , то выделяя полный квадрат по х, получим
, то выделяя полный квадрат по х, получим

Осуществим параллельный перенос:
|
|
|

тогда исходное уравнение принимает вид
 (3.48)
(3.48)
3) Если  ,
,  ,
,  , то, выделяя полный квадрат по х, получим
, то, выделяя полный квадрат по х, получим
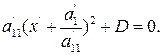
Осуществим параллельный перенос:

тогда исходное уравнение принимает вид:
 (3.49)
(3.49)
Классификация кривых второго порядка.
I. Рассмотрим уравнение (3.46) 
а) если  одного знака, уравнение называется уравнением эллиптического типа;
одного знака, уравнение называется уравнением эллиптического типа;
1) если D имеет другой знак, то при делении на –D получаем
 – каноническое уравнение эллипса;
– каноническое уравнение эллипса;
2) если D=0, уравнение  имеет единственное решение
имеет единственное решение  , определяющее точку на плоскости или пару мнимых пересекающихся прямых;
, определяющее точку на плоскости или пару мнимых пересекающихся прямых;
3) если знак D противоположен знаку  , уравнение после деления на D примет вид:
, уравнение после деления на D примет вид:
 .
.
Множество его решений пусто (иногда это пустое множество называют мнимым эллипсом).
б) если  разных знаков, то (3.47) называется уравнением гиперболического типа;
разных знаков, то (3.47) называется уравнением гиперболического типа;
1) при  оно сводится к одному из двух видов:
оно сводится к одному из двух видов:
 или
или  , в зависимости от знака D. Оба этих уравнения определяют гиперболу.
, в зависимости от знака D. Оба этих уравнения определяют гиперболу.
2) при D=0 получаем уравнение  эквивалентное двум линейным уравнениям
эквивалентное двум линейным уравнениям  и
и  , задающим пару пересекающихся прямых.
, задающим пару пересекающихся прямых.
|
|
|
II. Рассмотрим уравнение (3.48), после деления на  получим уравнение
получим уравнение  , определяющее параболу.
, определяющее параболу.
III. Рассмотрим уравнение (3.49):
1) если  разных знаков, то его можно привести к уравнению
разных знаков, то его можно привести к уравнению  или
или  , задающему пару параллельных прямых;
, задающему пару параллельных прямых;
2) если  одного знака, то уравнение можно привести к виду, не имеющему решений и, следовательно, не определяющему никакого геометрического образа (иногда это пустое множество называют пара мнимых параллельных прямых);
одного знака, то уравнение можно привести к виду, не имеющему решений и, следовательно, не определяющему никакого геометрического образа (иногда это пустое множество называют пара мнимых параллельных прямых);
3) если D = 0, то уравнение преобразуется к уравнению  , определяющему одну прямую (или пару слипшихся прямых).
, определяющему одну прямую (или пару слипшихся прямых).
Пример 3.9.
Найти каноническое уравнение линии второго порядка:
5x2 + 12xy – 22x – 12y – 19 = 0.
Решение.
Найдём угол поворота по формуле (3.45)

Осуществим поворот по формулам 
тогда уравнение примет вид:
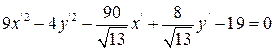 или
или 
После параллельного переноса 
получим 9Х2–4У2=36 или  .
.
Это уравнение гиперболы с полуосями, соответственно, 2 и 3 и центром (  ). Координаты центра в исходной системе координат х = 1, y = 1.
). Координаты центра в исходной системе координат х = 1, y = 1.
Поверхности второго порядка
Определение 3.5.1 Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида:
|
|
|
 (3.50)
(3.50)
- уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.
При переходе к ортонормированному базису собственных векторов исчезают все смешанные произведения переменных, и можно получить следующую классификацию поверхностей второго порядка:
I. Если  , то уравнение преобразуется к виду
, то уравнение преобразуется к виду
 (3.51)
(3.51)
и его можно привести к одному из следующих видов:
1) если  – одного знака, то уравнение (3.51) есть уравнение эллиптического типа и приводится к канонической форме
– одного знака, то уравнение (3.51) есть уравнение эллиптического типа и приводится к канонической форме
а) если D такого же знака
 (3.52)
(3.52)
- каноническое уравнение эллипсоида (рис. 3.16).
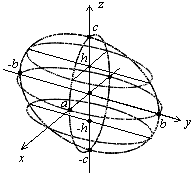
Рис. 3.16. Эллипсоид
Замечание. Если хотя бы два коэффициента совпадают, эллипсоид называется эллипсоидом вращения и представляет собой поверхность, полученную в результате вращения эллипса вокруг одной из его осей. Если все коэффициенты равны, уравнение (3.51) становится уравнением сферы.
Пример 3.10.
Нарисуйте сферу  .
.
Решение.
Выделив полные квадраты, получим  . Значит, центром сферы является точка М0(1; –2; 1), радиус сферы равен 2 (рис. 3.16).
. Значит, центром сферы является точка М0(1; –2; 1), радиус сферы равен 2 (рис. 3.16).
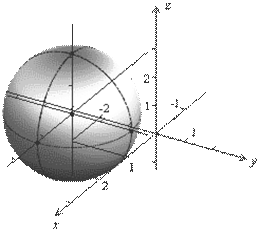
Рис. 3.17. Сфера
б) если D = 0, получим следующее уравнение  (3.53)
(3.53)
- уравнение задает точку в пространстве или мнимый конус;
в) если D другого знака, уравнение имеет вид  (3.54)
(3.54)
- пустое множество или мнимый эллипсоид.
2. Если  разных знаков, уравнение (3.51) приводится к виду:
разных знаков, уравнение (3.51) приводится к виду:
а) 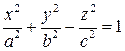 - уравнение однополостного гиперболоида (3.55)
- уравнение однополостного гиперболоида (3.55)

Рис. 3.18. Однополостный гиперболоид
б)  - уравнение двуполостного гиперболоида (3.56)
- уравнение двуполостного гиперболоида (3.56)

Рис. 3.19. Двуполостный гиперболоид
в)  - уравнение конуса второго порядка (3.57)
- уравнение конуса второго порядка (3.57)

Рис. 3.20. Конус
II. Одно из чисел  равно 0. Например,
равно 0. Например,  . При этом с помощью преобразований координат можно получить следующие формы уравнения (3.50):
. При этом с помощью преобразований координат можно получить следующие формы уравнения (3.50):
а) 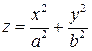 - уравнение эллиптического параболоида (3.58)
- уравнение эллиптического параболоида (3.58)

Рис. 3.21. Эллиптический параболоид
Если a=b, то сечения плоскостями, параллельными плоскости Oxy, являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости Oyz, вокруг оси Oz (рис. 3.22).
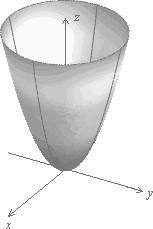
Рис. 3.22. Параболоид вращения
б) 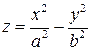 - уравнение гиперболического параболоида (3.59)
- уравнение гиперболического параболоида (3.59)

Рис. 3.23. Гиперболический параболоид (седло)
III. Если одно из чисел  равно 0. Например,
равно 0. Например,  , тогда получаем такую же классификацию, как у кривых второго порядка на плоскости. Рассмотрим реально существующие поверхности:
, тогда получаем такую же классификацию, как у кривых второго порядка на плоскости. Рассмотрим реально существующие поверхности:
а)  - эллиптический цилиндр (рис. 3.24). (3.60)
- эллиптический цилиндр (рис. 3.24). (3.60)

Рис.3.24. Эллиптический цилиндр
б)  - гиперболический цилиндр (рис. 3.25). (3.61)
- гиперболический цилиндр (рис. 3.25). (3.61)

Рис. 3.25. Гиперболический цилиндр
в)  - пара пересекающихся плоскостей. (3.62)
- пара пересекающихся плоскостей. (3.62)
г)  параболический цилиндр (рис. 3.26). (3.63)
параболический цилиндр (рис. 3.26). (3.63)

Рис. 3.26. Параболический цилиндр
д) 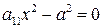 - пара параллельных плоскостей. (3.64)
- пара параллельных плоскостей. (3.64)
е)  - пара слипшихся плоскостей. (3.65)
- пара слипшихся плоскостей. (3.65)
Дата добавления: 2018-11-24; просмотров: 423; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
