Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.

Аналитическая геометрия

Линии на плоскости и их уравнения

Пусть на плоскости задана декартова система координат и некоторая линия l.

Определение 1. Уравнение

                          F (х,у) = 0                                                           (3.1)

называется уравнением линии l, если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии l, и не удовлетворяют координаты ни одной точки, не лежащей на линии l.

Пример 3.1.

(х – а)² + (y – b)² = R² – уравнение окружности радиуса R с центром в точке (a , b).

Замечание. Часто удобно использовать параметрические уравнения линии:

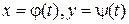                   ,                                                    (3.2)

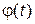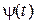где функции  и  непрерывны по параметру t.

 

Уравнение прямой на плоскости

Рассмотрим различные виды уравнений прямой на плоскости.

Пусть прямая проходит через точку М₀( x₀, y₀) перпендикулярно вектору n=(А, B ). Тогда вектор 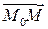, где М(х,у) – произвольная точка прямой, ортогонален n. Поэтому координаты любой точки данной прямой удовлетворяют уравнению

                      А(х – х₀) + В(у – у₀) = 0,                                      (3.3)        

которое является уравнением прямой, проходящей через данную точку перпендикулярно данному вектору.

Замечание. Вектор n называется нормалью к прямой.

Преобразуем уравнение (3.3) к виду:

                Ах + Ву + (–Ах₀ – Ву₀) = 0.

Обозначив –Ах₀ – Ву₀ = С, получим общее уравнение прямой:

                                 Ах + Ву + С = 0.                                        (3.4)                                       

 

Теперь получим уравнение прямой, проходящей через точку М₀( x₀, y₀) параллельно вектору s=( m , n ). Так как вектор 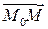, где М(х,у) – произвольная точка прямой, коллинеарен s, координаты любой точки данной прямой удовлетворяют уравнению

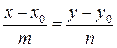                         ,                                               (3.5)

называемому каноническим уравнением прямой. Вектор s при этом называется направляющим вектором прямой. В частности, если прямая проходит через точки М₁(х₁,у₁) и М₂(х₂,у₂), ее направляющим вектором можно считать 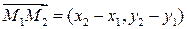, и из уравнения (3.5) следует:

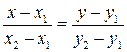                                                                                      (3.6)

– уравнение прямой, проходящей через две заданные точки.

Пример 3.2.

Составим уравнение прямой, проходящей через точки М(1,2) и N(5,–3). Уравнение (3.6) примет вид:

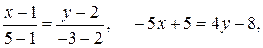
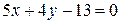  – общее уравнение прямой.

 

Обозначив за t значения равных дробей, стоящих в левой и правой частях уравнения (3.5), можно преобразовать это уравнение к виду:

                 x = x₀ + mt , y = y₀ + nt                                            (3.7)            

это параметрические уравнения прямой.

 

Для прямой l, не параллельной оси Оу, можно ввести так называемый угловой коэффициент k – тангенс угла, образованного прямой и осью Ох, и записать уравнение прямой в виде:

                        у = kx + b                                                         (3.8)     

это уравнение прямой с угловым коэффициентом.

Действительно, все точки прямой l₁, параллельной l и проходящей через начало координат, удовлетворяют уравнению у = k х, а ординаты соответствующих точек на прямой l отличаются от них на постоянную величину b.

Неполные уравнения прямой.

Определение 3.2.1. Уравнение (3.4) называется полным, если коэффициенты А, В и С не равны нулю, и неполным, если хотя бы одно из этих чисел равно нулю.

Рассмотрим возможные виды неполных уравнений прямой:

1) С = 0 – прямая Ах + Ву = 0 проходит через начало координат.

2) В = 0 – прямая Ах + С = 0 параллельна оси Оу (так как нормаль к прямой (A,0) перпендикулярна оси Оу).

3) А = 0 – прямая Ву + С = 0 параллельна оси Ох.

4) В = С = 0 – уравнение Ах = 0 определяет ось Оу.

5) А = С = 0 – уравнение Ву = 0 определяет ось Ох.

Таким образом, прямая, задаваемая полным уравнением, не проходит через начало координат и не параллельна координатным осям.

Преобразуем полное уравнение прямой следующим образом:

           Ах + Ву + С = 0 |:(–C),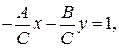   

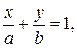                                                                                     (3.9)

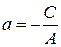где  и 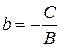 равны величинам отрезков, отсекаемых прямой на осях Ох и Оу. Поэтому уравнение (3.9) называют уравнением прямой в отрезках.

Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.

1. Если прямые l₁ и l₂заданы общими уравнениями

А₁х + В₁у + С₁ = 0 и А₂х + В₂у + С₂ = 0,

то угол между ними равен углу между их нормалями, то есть между векторами (A₁, B₁) и (A₂, B₂). Следовательно,

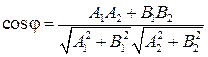                                                                    (3.10)

Условия параллельности и перпендикулярности прямых тоже сводятся к условиям параллельности и перпендикулярности нормалей:

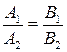 – условие параллельности,                                            (3.11)

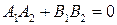 – условие перпендикулярности                      (3.12)

 

2. Если прямые заданы каноническими уравнениями (3.5), по аналогии с пунктом 1 получим:

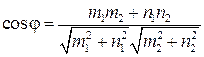      ,                                              (3.13)

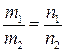       – условие параллельности,                               (3.14)

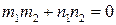       – условие перпендикулярности.            (3.15)

 

Здесь 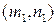 и  – направляющие векторы прямых.

 

Пусть прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами вида (4.8) у = k₁x + b₁ и y = k₂x + b₂, где 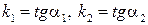, а α₁ и α₂ – углы наклона прямых к оси Ох, то для угла  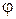между прямыми справедливо равенство:

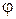 = α₂– α₁. Тогда

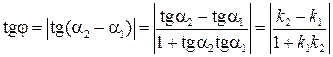                                         (3.16)

Условие параллельности имеет вид: k₁ = k₂,                                        (3.17)

условие перпендикулярности: k₁ · k₂ = –1,                                           (3.18)

поскольку при этом tg 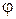 не существует.

---

Дата добавления: 2018-11-24; просмотров: 284; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!