Средняя арифметическая величина и ее свойства.
Средняя арифметическая (простая) используется в тех случаях, когда данные не сгруппированы.
Средняя арифметическая (взвешенная). При расчете отдельные значения признака могут встречаться несколько раз. Расчет производится по сгруппированным данным или вариационным рядам.
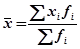
Свойства средней арифметической:
1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты.
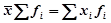
2. Сумма отклонений индивидуального значения признака от средней равно 0.
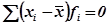
3. Если все осредняемые варианты увеличить или уменьшить на постоянное число А, то значение средней также увеличится или уменьшится на число А.
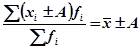
4. Если все варианты значений признака увеличить или уменьшить в А раз, то значение средней увеличится или уменьшится соответственно в А раз.
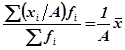
5. Если все частоты уменьшить или увеличить в А раз, то средняя не изменится.
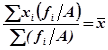
6. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С.
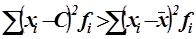
Средняя гармоническая, средняя квадратическая и средняя геометрическая величины.
1. Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Если в смысловой формуле ( 
не известен знаменатель, то в расчетах используется средняя гармоническая. Средняя гармоническая простая:
|
|
|
Средняя гармоническая взвешенная применяется тогда, когда статистическая информация не содержит отдельных частот по отдельным вариантам совокупности, а представлена как их произведение:
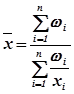
2. Средняя квадратическая применяется тогда, когда вместо отдельных значений признака представлены квадраты исходных величин.
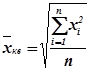
3. Средняя геометрическая применяется в случаях определения средней по значениям, имеющим большой разброс, либо в случаях определения средней по относительным показателям.
Структурные средние величины.
Характеристиками структуры совокупности являются мода и медиана.
1. Мода (М0) – величина признака, наиболее часто встречающегося в совокупности, т е имеющая наибольшую численность в ряду распределения.
А) В дискретном ряду мода определяется визуально.
Б) В интервальном ряду визуально можно определить интервал, в котором находится мода (модальный интервал).
,
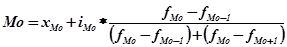где хМо – нижняя граница модального интервала;
i Мо – величина модального интервала;
f Мо – частота модального интервала;
f Мо-1 – частота, предшествующая модальному интервалу;
f Мо+1 – частота интервала, следующего за модальным.
2. Медиана (Ме) – значение признака, приходящегося на середину ранжированного ряда, т е делящее ряд распределения на две равные части.
|
|
|
А) В дискретном ряду определяется номер медианы по формуле:
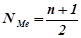
Номер медианы показывает то значение показателя, которое является медианой.
Б) В интервальном ряду медиана рассчитывается по формуле:
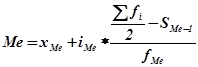
где хМе – нижняя граница медианного интервала;
i Ме – величина медианного интервала;
f Ме – частота медианного интервала;
SМе-1 – сумма накопленных частот, предшествующих медианному интервалу;
å fi /2 – полусумма частот ряда.
Показатели вариации.
Основными показателями, характеризующими вариацию, являются: размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации.
Размах вариации – разность между максимальным и минимальным значением признака.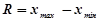 
Среднее линейное отклонение – это средний модуль отклонений значений признака от средней величины.
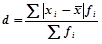
Дисперсия – средний квадрат отклонений значений признака от их средней величины.
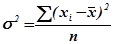простая 
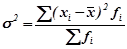взвешенная
Среднее квадратическое отклонение представляет собой квадратный корень из дисперсии.
Эти четыре показателя позволяют получить абсолютное значение вариации, т е оценивают вариацию в единицах измерения исследуемой совокупности.
|
|
|
Коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня.
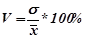
Если коэффициент рассматриваемой совокупности не превышает 33%, то ее можно считать однородной по рассматриваемому признаку.
Показатели вариации используются для:
1) анализа изменчивости изучаемого признака
2) оценки степени воздействия одного признака на вариацию другого
При проведении такого анализа совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным и результативным.
Дата добавления: 2018-11-24; просмотров: 2077; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!