Типовой разбор варианта контрольной работы № 1
Правила выполнения и оформления
Контрольных работ
При выполнении контрольных работ необходимо придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 1-2 см для замечаний рецензента.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер – последняя цифра в зачетке, название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не засчитываются.
4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
|
|
|
7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Контрольная работа № 1
Вариант 0 | |||||||||||||||
| 1 | Среди 25 студентов, где 10 девушек, разыгрываются 5 билетов в кино. Определить вероятность того, что среди обладателей билетов окажутся 1) две девушки, 2) хотя бы одна девушка. | ||||||||||||||
| 2 | Рабочий обслуживает три станка, работающих независимо друг от друга. Пусть событие  означает, что в течение часа не потребует внимания рабочего i-ый станок. Вероятности соответственно равны означает, что в течение часа не потребует внимания рабочего i-ый станок. Вероятности соответственно равны  , , 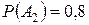 , ,  . Событие В состоит в том, что в течение часа один станок потребует внимания рабочего, событие С – в течение часа три станка не потребуют внимания рабочего. Написать формулу выражающую события В и С через события . Событие В состоит в том, что в течение часа один станок потребует внимания рабочего, событие С – в течение часа три станка не потребуют внимания рабочего. Написать формулу выражающую события В и С через события  и вычислить вероятности этих событий. и вычислить вероятности этих событий.
| ||||||||||||||
| 3 | В первой партии – 100 деталей. Вероятность брака в этой партии равна 0,01. Во второй партии – 200 деталей, вероятность брака – 0,005. Найти вероятность того, что в обеих партиях нет бракованных деталей. Вычислить: 1) эту вероятность по формуле Бернулли; 2) ту же вероятность с помощью формулы Пуассона. | ||||||||||||||
| 4 |
СВ
Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти: 1) параметр С и построить график
Найти: 1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(0,5< X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(0,5< X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||||
| 7 | Заданы математическое ожидание 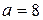 и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность 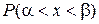 ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||||
Вариант 1
| |||||||||||||||
| 1 | В 25 экзаменационных билетах содержатся по три вопроса, которые не повторяются. Студент знает ответы на 45 вопросов. Какова вероятность того, что 1) доставшийся билет состоит из подготовленных им вопросов, 2) хотя бы один вопрос подготовлен? | ||||||||||||||
| 2 | На наблюдательной станции установлено четыре радиолокатора различных конструкций. Пусть событие  означает обнаружение цели с помощью i-ого локатора. Вероятности соответственно равны означает обнаружение цели с помощью i-ого локатора. Вероятности соответственно равны  , , 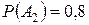 , ,  , ,  . Событие В состоит в том, что все четыре локатора обнаружат цель; событие С – один локатор обнаружит цель. Написать формулу выражающую события В и С через события . Событие В состоит в том, что все четыре локатора обнаружат цель; событие С – один локатор обнаружит цель. Написать формулу выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||||
| 3 | Вероятность появления опечатки на странице книги, содержащей 100 страниц, равна 0,03. Найти вероятность того, что в книге имеется не более двух опечаток: 1) по биномиальной формуле; 2) по формуле Пуассона. | ||||||||||||||
| 4 |
СВ
Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение 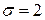 нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность 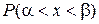 ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||
Вариант 2 | |||||||||||||
| 1 | Из партии, состоящей из 20 радиоприемников, для проверки произвольно отбирают три приемника. Партия содержит пять неисправных приемников. Какова вероятность того, что в число отобранных войдут 1) один неисправный и два исправных радиоприемника; 2) хотя бы один исправный радиоприемник? | ||||||||||||
| 2 | Вероятность попадания в мишень при одном выстреле равна 0,6. По мишени стреляют одиночными выстрелами до первого попадания, после чего стрельбу прекращают. Пусть событие  означает попадание по мишени при i-ом выстреле. Событие В – попадание при втором выстреле; С - будет сделано не более двух выстрелов. Написать формулу выражающую события В и С через события означает попадание по мишени при i-ом выстреле. Событие В – попадание при втором выстреле; С - будет сделано не более двух выстрелов. Написать формулу выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||
| 3 | Вероятность, того что любой абонент позвонит на коммутатор в течении часа, равна 0,07. Телефонная станция обслуживает 100 абонентов. Какова вероятность того, что в течение часа позвонят не более двух абонентов. Вычислить эту вероятность с помощью 1) формулы Бернулли; 2) формулы Пуассона. | ||||||||||||
| 4 |
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание 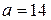 и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||
Вариант 3 | |||||||||||||
| 1 | В партии из 15 деталей имеются 4 бракованных. Какова вероятность того, что среди наудачу отобранных 5 деталей окажутся 1) две бракованными; 2) хотя бы одна бракованная? | ||||||||||||
| 2 | Испытываются 3 прибора на надежность. Пусть событие  означает выход из строя i-ого прибора. Вероятности соответственно равны означает выход из строя i-ого прибора. Вероятности соответственно равны  , , 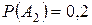 , ,  . Событие В состоит в том, что из строя вышло не менее двух приборов, событие С – все приборы работают. Написать формулу выражающую события В и С через события . Событие В состоит в том, что из строя вышло не менее двух приборов, событие С – все приборы работают. Написать формулу выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||
| 3 | Устройство содержит 100 одинаковых деталей 1-го типа и 100 деталей 2-го типа. По прошествии времени Т каждая деталь 1-го типа выходит из строя с вероятностью  , а каждая деталь 2-го типа – с вероятностью , а каждая деталь 2-го типа – с вероятностью  (детали работают независимо друг от друга). Найти вероятность того, что через время Т выйдет из строя не более одной детали 1-го типа и ни одной детали 2-го типа. Вычислить эту вероятность с помощью 1) формулы Бернулли; 2) формулы Пуассона. (детали работают независимо друг от друга). Найти вероятность того, что через время Т выйдет из строя не более одной детали 1-го типа и ни одной детали 2-го типа. Вычислить эту вероятность с помощью 1) формулы Бернулли; 2) формулы Пуассона.
| ||||||||||||
| 4 |
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти: 1) параметр С и построить график
Найти: 1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность 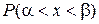 ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||
Вариант 4 | |||||||||||||
| 1 | Из партии, в которой 30 микросхем без дефекта и 5 с дефектами, берут наудачу 3 микросхемы. Найти вероятность того, что 1) две микросхемы без дефекта; 2) по крайней мере одна микросхема без дефекта. | ||||||||||||
| 2 | По самолету производится 3 выстрела. Пусть событие  - это попадание при i-ом выстреле. Вероятность - это попадание при i-ом выстреле. Вероятность 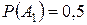 , ,  , ,  . Событие В состоит в том, что только при третьем выстреле будет попадание; событие С – самолет будет сбит, если для этого достаточно двух попаданий. Написать формулу выражающую события В и С через события . Событие В состоит в том, что только при третьем выстреле будет попадание; событие С – самолет будет сбит, если для этого достаточно двух попаданий. Написать формулу выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||
| 3 | Вероятность брака детали равна 0,05. После изготовления деталь осматривается контролером, который обнаруживает брак с вероятностью 0,95. Найти вероятность того, что из 100 проверенных деталей забракованных окажется не более одной. Вычислить: 1) эту вероятность с помощью формулы Бернулли, 2) эту же вероятность с помощью формулы Пуассона. | ||||||||||||
| 4 |
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X > 1) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X > 1) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  . .
| ||||||||||||
Вариант 5 | |||||||||||||
| 1 | В новогодней лотерее 25 билетов, 10 из которых выигрывают. Гражданин купил 4 билетов. Какова вероятность того, что 1) три будут выигрышными; 2) по крайне мере один из купленных билетов выигрышный? | ||||||||||||
| 2 | Пусть событие  - бесперебойная работа i-го химического реактора в течении суток. Вероятности соответственно равны - бесперебойная работа i-го химического реактора в течении суток. Вероятности соответственно равны  , ,  . Событие В состоит в том, что оба реактора в течении суток будут бесперебойно работать; событие С – будет работать бесперебойно в течение суток только один реактор. Написать формулу выражающую события В и С через события . Событие В состоит в том, что оба реактора в течении суток будут бесперебойно работать; событие С – будет работать бесперебойно в течение суток только один реактор. Написать формулу выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||
| 3 | а) Вероятность того, что часы, сданные в ремонт, будут отремонтированы в срок, равна 0,9. Определить по формуле Бернулли вероятность того, что из восьми сданных в ремонт часов более шести будут отремонтированы в срок. б) Вероятность того, что часы после ремонта сломаются, равна 0,02. Определить по формуле Пуассона вероятность того, что из 100 отремонтированных часов не более двух выйдут из строя. | ||||||||||||
| 4 |
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X >1,5) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X >1,5) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||
Вариант 6 | |||||||||||||
| 1 | В оперотряде 10 человек, среди них 7 мужчин. На исследование места аварии направляется группа из 6 человек. Найти вероятность того, что в группе будет: 1) 4 мужчины; 2) хотя бы одна женщина? | ||||||||||||
| 2 | В устройстве три блока, от работы которых зависит работа всего устройства. Пусть событие  – это безотказная работа i-ого блока. Вероятности соответственно равны – это безотказная работа i-ого блока. Вероятности соответственно равны  , ,  , , 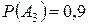 . Событие В состоит в том, что первый блок работает, а третий вышел из строя; событие С – работа устройства, если для этого достаточно безотказная работа двух блоков. Написать формулу выражающую события В и С через события . Событие В состоит в том, что первый блок работает, а третий вышел из строя; событие С – работа устройства, если для этого достаточно безотказная работа двух блоков. Написать формулу выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||
| 3 | По радиоканалу передано n =200 сообщений. Вероятность искажения каждого сообщения помехами равна 0,005. Вычислить: 1) с помощью формулы Бернулли вероятность того, что при передаче будет искажено более двух сообщений; 2) ту же вероятность по формуле Пуассона. | ||||||||||||
| 4 |
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||
| 5 | Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для 1-го стрелка – 0,4, для 2-го – 0,7. СВ  – сумма числа попаданий двумя стрелками. Составьте закон распределения – сумма числа попаданий двумя стрелками. Составьте закон распределения  и постройте многоугольник распределения, найдите математическое ожидание и постройте многоугольник распределения, найдите математическое ожидание  и дисперсию и дисперсию  этой СВ. Найдите вероятности событий: а) А – сумма очков не менее 2; б) В – сумма очков более одного. этой СВ. Найдите вероятности событий: а) А – сумма очков не менее 2; б) В – сумма очков более одного.
| ||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(0,5<X <2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(0,5<X <2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||
Вариант 7 | |||||||||||||
| 1 | В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов для проверки остаточных знаний. Найти вероятность того, что среди отобранных студентов: 1) 5 отличников; 2) хотя бы один не отличник. | ||||||||||||
| 2 | Событие  состоит в том, что состоит в том, что  -е предприятие своевременно выполнило задание -е предприятие своевременно выполнило задание  . Вероятности этих событий соответственно равны: . Вероятности этих событий соответственно равны:  Событие В – только одно предприятие справилось с заданием. Событие С – все три предприятия справились с заданием. Написать формулу выражающую события В и С через события Событие В – только одно предприятие справилось с заданием. Событие С – все три предприятия справились с заданием. Написать формулу выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||
| 3 | В партии п =100 деталей. Вероятность брака детали равна р =0,02. Найти: 1) с помощью формулы Бернулли вероятность того, что в партии не более двух бракованных деталей; 2) ту же вероятность с помощью формулы Пуассона. | ||||||||||||
| 4 |
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||
|
Вариант 8 | |||||||||||||
| 1 | В ящике 5 новых и 7 старых инструментов. Рабочему выдали 3 инструмента. Найти вероятность того, что: 1) два из трех выданных инструментов старые; 2) хотя бы один из трех инструментов новый. | ||||||||||||
| 2 | Диспетчер принимает вызовы с трех объектов, функционирующих независимо друг от друга. Событие  означает, что в течение смены придет вызов с i-го объекта. Вероятности соответственно равны: означает, что в течение смены придет вызов с i-го объекта. Вероятности соответственно равны:  Событие В – в течение смены не будет вызов со объектов; событие С – в течение смены придет вызов хотя бы с двух объектов. Написать формулу, выражающую события В и С через события Событие В – в течение смены не будет вызов со объектов; событие С – в течение смены придет вызов хотя бы с двух объектов. Написать формулу, выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||
| 3 | Вероятность, того что телевизор потребует ремонта в течение гарантийного срока, равна 0,05. Найти вероятность того, что в течение гарантийного срока не более двух потребуют ремонта: 1) из 20 телевизоров по формуле Бернулли; 2) из 200 телевизоров по формуле Пуассона. | ||||||||||||
| 4 |
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(0,5< X < 4) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(0,5< X < 4) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание 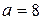 и среднее квадратичное отклонение и среднее квадратичное отклонение 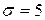 нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||
Вариант 9 | |||||||||||||
| 1 | Имеется серия из 20 образцов данного вида продукции. Из них 10 образцов первого сорта, 8 – второго и 2 нестандартных. Найти вероятность того, что среди пяти образцов, отобранных случайным образом из серии: 1) 3 окажутся первого сорта и 2 – второго; 2) по крайне мере одно нестандартное. | ||||||||||||
| 2 | Вероятность того, что абитуриент выполнит работу по математике на положительную оценку (событие  ), равна 0,6, по физике (событие ), равна 0,6, по физике (событие  ) равна 0,5, по русскому языку (событие ) равна 0,5, по русскому языку (событие  ) – 0,7. Событие В – абитуриент сдаст все работы на положительную оценку. Событие С – абитуриент один предмет не выполнит на положительную оценку. Написать формулу, выражающую события В и С через события ) – 0,7. Событие В – абитуриент сдаст все работы на положительную оценку. Событие С – абитуриент один предмет не выполнит на положительную оценку. Написать формулу, выражающую события В и С через события  и вычислить вероятность этих событий. и вычислить вероятность этих событий.
| ||||||||||||
| 3 | На каждом станке за смену выпускается п деталей. Вероятность брака для первого станка равна р1, для второго – р2. Найти вероятность того, что в сменной продукции обоих станков не более одной бракованной детали. Вычислить эту вероятность: 1) при n = 8, p1 = 0,05, p2 = 0,03 по формуле Бернулли; 2) при n =100, p1 = 0,005, p2 = 0,003 по формуле Пуассона. | ||||||||||||
| 4 |
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность | ||||||||||||
| 6 | Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти: 1) параметр С и построить график
Найти: 1) параметр С и построить график  ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(–1< X < 3) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F(x)и построить ее график;
3) математическое ожидание mX , дисперсию DX и среднее квадратическое отклонение s(x);
4) вероятность Р(–1< X < 3) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| ||||||||||||
| 7 | Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| ||||||||||||
Типовой разбор варианта контрольной работы № 1
Задание 1.
В цехе работают 6 мужчин и 4 женщины. Отбирается делегация из 7 человек на собрание. Найти вероятность того, что в делегации: 1) окажутся 3 женщины, 2) окажется хотя бы одна женщина.
Решение.
1) Событие А – в делегации из 7 человек окажутся 3 женщины, следовательно, в делегации будет 4 мужчины.
Для данного события порядок выбора не важен, важен только состав делегации. Используем формулы комбинаторики: число сочетаний  .
.
 – число способов выбора 3 женщин из 4;
– число способов выбора 3 женщин из 4;
 – число способов выбора 4 женщин из 6.
– число способов выбора 4 женщин из 6.
Благоприятных исходов  .
.
Всего исходов  (число способов выбора 7 человек из 10).
(число способов выбора 7 человек из 10).
Поэтому  .
.
2) Пусть событие В – в делегации из 7 человек окажется хотя бы одна женщина.
Для вычисления вероятности этого события перейдем к противоположному событию
 ,
,
т.к. благоприятные исходы  - число способов выбора 7 мужчин из 7; всего исходов
- число способов выбора 7 мужчин из 7; всего исходов 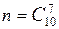 (число способов выбора 7 человек из 10).
(число способов выбора 7 человек из 10).
Ответ:  ,
,  .
.
Задание 2.1.
Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй – 0,8, третий – 0,7. Пусть события  – студент сдаст i-ый экзамен
– студент сдаст i-ый экзамен  .
.
Написать формулу, выражающую следующие события через события 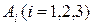 и вычислить вероятность этих событий:
и вычислить вероятность этих событий:
а) событие В - студент будет сдан только 2–ой экзамен;
б) событие С - студентом будет сдан только один экзамен;
в) событие D - студентом будут сданы три экзамена;
г) событие E - студентом будет сдано два экзамена;
д) событие F - студентом будет сдан хотя бы один экзамен.
Решение.
Т.к. события  – студент сдаст i-ый экзамен
– студент сдаст i-ый экзамен  , тогда вероятности
, тогда вероятности
| i | сдачи экзаменов

| не сдачи экзаменов

|
| 1 | 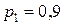
| 
|
| 2 | 
| 
|
| 3 | 
| 
|
а) Событие В – студент сдаст только 2-ой экзамен состоит в том, что студент сдаст 2-ой экзамен и не сдаст 1-ый и 3-ий экзамены, т.е. 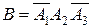 , учитывая что события независимы, получим
, учитывая что события независимы, получим
 .
.
б) Событие С – студент сдаст один экзамен из трех, т.е. сдаст или 1-й экзамен из трех, или 2-й, или 3-й из трех экзаменов. Следовательно, событие  .
.
Т.к. события  несовместны, то
несовместны, то


в) Событие D – студент сдаст все три экзамена, т.е.  . Тогда
. Тогда
 .
.
г) Событие Е – студент сдаст два экзамен из трех, т.е. не сдаст или 1-й экзамен из трех, или 2-й, или 3-й из трех экзаменов.
Следовательно, событие  . Т. к. события
. Т. к. события  несовместны, то
несовместны, то
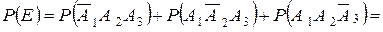

д) Пусть событие F – студент сдаст хотя бы один экзамен. Удобнее записать это событие, если перейти к противоположному событию: 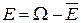 .
.
Противоположное событие  заключается в том, что студент не сдаст ни один экзамен, т.е. и 1-й не сдаст, и 2-й не сдаст, и 3-й не сдаст.
заключается в том, что студент не сдаст ни один экзамен, т.е. и 1-й не сдаст, и 2-й не сдаст, и 3-й не сдаст.
Значит, событие  и вероятность данного события равна
и вероятность данного события равна
 .
.
Ответ: а)  ,
,  ;
;
б)  ,
,  ;
;
в)  ,
,  ;
;
г)  ,
, 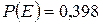 ;
;
д)  ,
,  .
.
Задание 2.2.
При включении зажигания двигатель начнет работать с вероятностью  . Пусть событие
. Пусть событие  двигатель начнет работать при i-ом включении зажигания. Событие В состоит в том, что двигатель начнет работать при третьем включении зажигания; С – для запуска двигателя придется включать зажигание не более трех раз.
двигатель начнет работать при i-ом включении зажигания. Событие В состоит в том, что двигатель начнет работать при третьем включении зажигания; С – для запуска двигателя придется включать зажигание не более трех раз.
Написать формулу выражающую события В и С через события  и вычислить вероятность этих событий.
и вычислить вероятность этих событий.
Решение.
Т. к. событие  – двигатель начнет работать при i -ом включении зажигания, то
– двигатель начнет работать при i -ом включении зажигания, то  .
.
Тогда событие В – двигатель начнет работать при третьим зажигании, следовательно, при 1-ом и при 2-ом зажигание не сработало. Событие В можно представить в виде  и вероятность этого события равна
и вероятность этого события равна
 .
.
Событие С – для запуска придется включать зажигание не более трех раз. Событие С – наступит, если двигатель начнет работать при 1-м, или при 2-м, или при 3-м включении, т.е.  и, следовательно, вероятность события С
и, следовательно, вероятность события С

Ответ:  ,
,  ;
;
 ,
, 
Задание 3.
Пусть вероятность того, что студент опоздает на лекцию, равна 0,08. Найти вероятность того, что среди 96 студентов на лекцию опоздает не более 3-х человек 1) по биномиальной формуле, 2) по формуле Пуассона.
Решение.
Решение задачи основывается на вычислении вероятностей  .
.
Событие А – «на лекцию опоздает не более 3-х человек» означает, что опоздает или 0, или 1, или 2, или 3 студента, т. е. k = 0, или k = 1, или k = 2, или k = 3.
Искомая вероятность определяется:
 .
.
Вычислим  разными способами.
разными способами.
1) по биномиальной формуле (формуле Бернулли):  ,
,
где  ,
,  .
.

2) Т. к.  ,
,  и
и 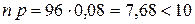 , то искомую вероятность можно вычислить по приближенной формуле Пуассона
, то искомую вероятность можно вычислить по приближенной формуле Пуассона
 , где
, где 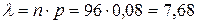 .
.
Вычисляем вероятность по формуле Пуассона

Таким образом, получаем
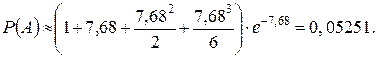
Ответ: а)  , б)
, б) 
| Задание 4. | 
| 1 | 2 | 3 |
СВ  задана законом распределения. задана законом распределения.
| 
| 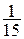
| ? | 
|
Найти:
1) числовые характеристики  ,
,  ;
;
2) функцию распределения 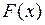 и построить ее график;
и построить ее график;
3) вероятность  .
.
Решение.
В задаче рассматривается дискретная СВ Х, заданная рядом распределения. По свойству ряда  Отсюда получаем
Отсюда получаем 
1) Математическое ожидание:
 .
.
Дисперсия:
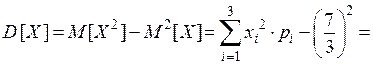
 .
.
Среднее квадратическое отклонение:  .
.
| 2) Функция распределения имеет вид (рис. 1):
| 
|
| Рис. 1 |
3)  .
.
Задание 6.
Плотность вероятности непрерывной СВ X задана функцией
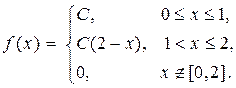
 Найти:
Найти:
| 1) | параметр С и построить график  ; ;
|
| 2) | интегральную функцию  и построить ее график; и построить ее график;
|
| 3) | математическое ожидание  , дисперсию , дисперсию  и среднее квадратическое отклонение и среднее квадратическое отклонение 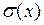 ; ;
|
| 4) | вероятность  дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
|
Решение.
Данный закон распределения является непрерывным.
1) По свойству плотности (дифференциальной функции):
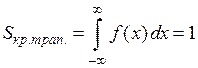




 .
.
Получаем функцию:
|
|
и ее график (рис. 3). | 
|
| Рис. 3 |
2) Найдём интегральную функцию, учитывая свойства:
· если  , то
, то  ;
;
· если 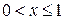 , то
, то
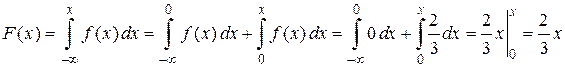 ;
;
· если  , то
, то

 .
.
· если  , то
, то

 .
.
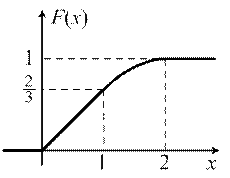
| В итоге получаем функцию и её график (рис. 4)
| 
|
| Рис. 4 |
3) Вычислим числовые характеристики:
· математическое ожидание:

 ;
;
· дисперсию по формуле  :
:

 ;
;
 ;
;
· среднее квадратическое отклонение: 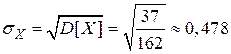 .
.
4) Найдём вероятность того, что СВ X примет значения из интервала  двумя способами:
двумя способами:
| q
Здесь вероятность численно равна площади выделенной фигуры (рис. 5). q В этом случае вероятность численно равна длине отрезка на оси При этом результаты вычислений совпадают при различных способах. | 
|
| Рис. 5 | |

| |
| Рис. 6 |
Ответ:  ;
; 
 ;
;  ;
; 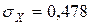 ;
;  .
.
Задание 7.
Заданы математическое ожидание  и среднее квадратическое отклонение
и среднее квадратическое отклонение  нормально распределенной непрерывной СВ.
нормально распределенной непрерывной СВ.
Найти:
1) вероятность  ;
;
2) вероятность  ;
;
3) симметричный, относительно  , интервал, в который попадает случайная величина
, интервал, в который попадает случайная величина  с вероятностью
с вероятностью  .
.
Дайте графические пояснения ответов на кривой нормального распределения ко всем пунктам.
Решение.
1) СВ X – распределена нормально с параметрами  .
.
Используем формулу  , где
, где  – функция Лапласа, ее значения табулированы (см. приложение).
– функция Лапласа, ее значения табулированы (см. приложение).
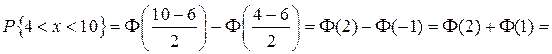
 .
.
| С графической точки зрения вероятность позволяет определить площадь фигуры, находящейся под графиком дифференциальной функции на указанном интервале. В данном случае (рис. 7):
| 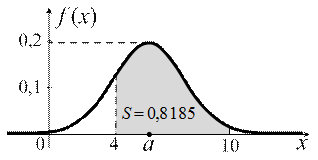
|
| Рис. 7 | |
| 2) Используем формулу
Тогда
Соответствующая фигура и ее площадь показаны на рис. 8. | 
|
| Рис. 8 | |
| 3) Имеем
| 
|
| Рис. 9 |
Искомый интервал имеет вид:  .
.
Итак получаем интервал:  (рис. 9).
(рис. 9).
Ответ:  ,
,  ,
,
 .
.
Дата добавления: 2018-11-24; просмотров: 4326; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!



 задана законом распределения.
задана законом распределения. ,
,  ;
; и построить ее график;
и построить ее график; .
. 
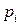
 ,
,  ;
;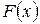 и построить ее график;
и построить ее график;
 задана законом распределения.
задана законом распределения. и построить ее график;
и построить ее график;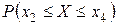 .
. 
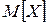 ,
,  ;
; .
. 
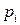
 ,
,  и построить ее график;
и построить ее график; .
.  и построить ее график;
и построить ее график;
 задана законом распределения.
задана законом распределения. и построить ее график;
и построить ее график; .
. 
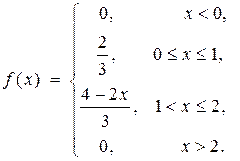



 .
.
 .
. (рис. 6).
(рис. 6). .
.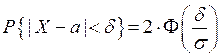 .
.
 .
. .
. , тогда
, тогда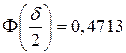 по таблице приложения значений функции Лапласа находим
по таблице приложения значений функции Лапласа находим 
 .
.