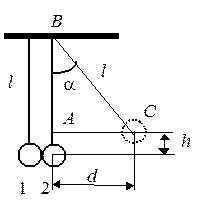Определение средней силы при соударении двух одинаковых шаров
Министерство образования Республики Беларусь Учреждение образования Международный государственный экологический университет им. А.Д. Сахарова Факультет мониторинга окружающей среды Кафедра физики и высшей математики
Лабораторная работа № 5
ИЗУЧЕНИЕ СТОЛКНОВЕНИЙ ШАРОВ.
ОПРЕДЕЛЕНИЕ ВРЕМЕНИ И СИЛЫ УДАРА.
ОПРЕДЕЛЕНИЕ МАСС ШАРОВ.
Минск
2013
Цель работы: исследовать центральные соударения шаров, определить время соударения, силу удара, массы шаров.
Приборы и оборудование: установка для изучения соударений шаров: платформа с закрепленными шариками, транспортир, набор шаров из разных материалов, вольтметр со встроенным конденсатором и источником питания; штангенциркуль, линейка.
1. Теоретическая часть:
Удар двух шаров
В механике под ударом следует понимать кратковременное взаимодействие двух или более тел, возникающее в результате их соприкосновения. Например, столкновение шаров, удар молота о наковальню, попадание пули в мишень и т.д. Если в результате удара механическая энергия не переходит в другие формы энергии, то удар называется идеально упругим. При ударе в течение кратковременного соприкосновения двух шаров происходит их деформация, точка соприкосновения переходит в круглую площадку. Кинетическая энергия ударяющегося тела переходит в энергию упругой деформации. При этом возникают упругие силы, возрастающие с увеличением деформации. В момент наибольшего сжатия шаров упругие силы максимальны. Потенциальная энергия деформации переходит в кинетическую энергию движения, пока шары не разойдутся. Идеальному упругому удару соответствует полное восстановление формы соударяющихся тел. Время соударения зависит от упругих констант материала шаров, их относительной скорости в момент начала удара и от их массы.
|
|
|
Другим предельным случаем является идеально неупругий удар. При этом после удара тела движутся с одинаковыми по величине и направлению скоростями.
Идеально упругих ударов в природе не существует, так как всегда часть энергии затрачивается на необратимую деформацию тел и увеличение их внутренней энергии. Однако для некоторых тел, например стальных шаров, потерями механической энергии можно пренебречь.
Если направление движения двух соударяющихся шаров в момент их соприкосновения совпадает с прямой, соединяющей центры шаров, то удар называется центральным.
На основании второго закона механики имеем
(1)
Если рассматривать последнее уравнение применительно к удару, то: 
- средняя сила удара, 
- время удара, т.е. время соприкосновения ударяющихся тел, 
- масса одного из соударяющихся тел (другое считаем неподвижным), 
- изменение скорости этого тела, возникшее в результате удара.
|
|
|
Из уравнения (1) следует, что чем меньше время соударения двух тел, тем больше сила удара при том же изменении скорости.
Определение средней силы при соударении двух одинаковых шаров
|
|
Рассмотрим систему, состоящую из двух шаров, подвешенных на практически нерастяжимых нитях (рис. 1). Массы шаров одинаковы ( 
). Отведем правый шар 2 на угол 
от положения равновесия и отпустим его. Возвращаясь в положение равновесия и обладая в момент, предшествующий удару, скоростью 
, он передает количество движения левому шару 1. Согласно закону сохранения количества движения запишем
(2)
где 
и 
- скорости шаров после удара.
Используя закон сохранения энергии, получим
(3)
Но так как 
, то последние уравнения перепишутся в виде
, 
(4)
отсюда
Так как под действием удара второй шар начал двигаться, то 
, тогда 
, т.е. при равенстве масс двух соударяющихся шаров, один из которых неподвижен, движущийся шар полностью передает количество движения неподвижному и останавливается. Из уравнения (4) следует что 
. Это значит, что шары как бы обмениваются скоростями.
|
|
|
Если второй шар после соударения остается в покое ( 
), то 
. Тогда формулу (1) можно переписать в виде
где 
- время удара. Отсюда
(5)
При известной массе шаров среднюю силу удара всегда можно вычислить, зная скорость шара 
в момент, непосредственно предшествующий соударению, и время соударения t .
Дата добавления: 2018-11-24; просмотров: 1353; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!