Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления и обратно.

 

1. Для перевода из двоичной системы счисления в восьмеричную необходимо разбить данное двоичное число на триады ( три цифры ) и представить каждую триаду в виде числа, которое является суммой соответствующих степеней двойки.. При невозможности разбиения на триады допускается добавление нулей слева записи числа. Для обратного перевода каждую цифру восьмеричного числа представляют соответствующей триадой двоичного кода.

 

1. Для перевода из двоичной системы счисления в шестнадцатеричную необходимо разбить данное двоичное число на тетрады ( четыре цифры ) и представить каждую тетраду в виде числа, которое является суммой соответствующих степеней двойки. При невозможности разбиения на тетрады допускается добавление нулей слева записи числа. Для обратного перевода каждую цифру шестнадцатеричного числа представляют соответствующей тетрадой двоичного кода.

 

Необходимо помнить!

a^o =1 (для любого а не равного нулю)

а¹=а

 

Степени двойки:

2⁰ = 1         2⁵ = 32

2¹ = 2         2⁶ = 64

2² = 4         2⁷ = 128

2³ = 8         2⁸= 256

2¹⁰= 1024

Алфавит шестнадцатеричной системы счисления:

0-9, А(10), В(11), С(12), D(13), E(14), F(15)

 

Задачи

Задача 1.

Число 22₁₀ перевести в двоичную систему счисления.

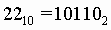
Задача 2.

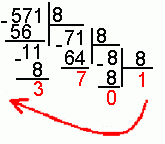
Число 571₁₀  перевести в восьмеричную систему счисления.

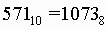
Задача 3.

Число 7467₁₀  перевести в шестнадцатеричную систему счисления.

 

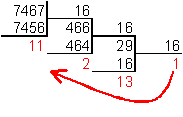
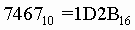
(необходимо помнить, что если при переводе из десятичной системы в шестнадцатеричную в остатке получили число большее 9, его надо заменить на соответствующую букву: в примере 13 заменяем на D)

Задача 4.

Число 10110110₂ перевести в десятичную систему счисления.

Решение.

В этом числе 8 цифр и 8 разрядов ( разряды считаются справа, начиная с нулевого). В соответствии с уже известным нам правилом представим его в виде суммы степеней с основанием 2:

10110110₂ = (1·2⁷)+(0·2⁶)+(1·2⁵)+(1·2⁴)+(0·2³)+(1·2²)+(1·2¹)+(0·2⁰) = 128+32+16+4+2 = 182₁₀

 

Задача 5.

Число 2357₈  перевести в десятичное.

Решение.

В этом числе 4 цифры и 4 разряда ( разряды считаются справа , начиная с нулевого). В соответствии с уже известным нам правилом представим его в виде суммы степеней с основанием 8:

2357₈ = (2·8³)+(3·8²)+(5·8¹)+(7·8⁰) = 2·512 + 3·64 + 5·8 + 7·1 = 1263₁₀

 

Задача 6.

Число D23C перевести в десятичное.

Решение.

В этом числе 4 цифры и 4разряда (помним, что разряды считаются справа, начиная с нулевого). В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:

D23C₁₆ = (13·16³)+(2·16²)+(3·16¹)+(12·16⁰) = 53820

(если шестнадцатеричное число содержит букву в вычислениях заменяем ее на числовой эквивалент)

Задача 7.

Перевести 11100110001000₂  в восьмеричную систему счисления

 

Решение.

Делим двоичное число на триады начиная справа 011 100 110 001 000 – слева дописываем незначащий нуль. Каждая цифра триады соответствует степени двойки (4 2 1). Для каждой триады складываем только те степени двойки, которые соответствуют цифре 1 в двоичной записи. Таким образом для первой триады (начинаем справа) в восьмеричной системе получаем цифру 0+0+0 = 0, для второй 0+0+1=1, для третьей 0+2+4=6, для четвертой 0+0+4=4 и для пятой 1+2+0=3.

 

11100110001000₂ = 34610₈

 

Задача 7.

Перевести 1101100101101000₂  в шестнадцатеричную систему счисления

 

Решение.

Делим двоичное число на тетрады начиная справа 1101 1001 0110 1000 (если ровно не делится дописываем справа незначащий нуль).. Каждая цифра тетрады соответствует степени двойки (8 4 2 1). Для каждой тетрады складываем только те степени двойки, которые соответствуют цифре 1 в двоичной записи. Таким образом для первой тетрады (начинаем справа) в шестнадцатеричной системе получаем цифру 0+0+0+8 = 8, для второй 0+4+2+0 =6, для третьей 8+0+0+1=9, для четвертой 8+4+0+1=13(D). Если получаем число большее 9 заменяем его на соответствующую букву в шестнадцатеричной системе счисления.

 

Задача 8.

Перевести 543₈ в двоичную систему счисления.

Решение.

Каждая цифра(разряд) числа в восьмеричной системе счисления соответствуют три цифры (разряда) в двоичной. Поэтому каждая цифра восьмеричного числа получается из суммы соответствующих степеней двойки (4 2 1), умноженных на 1 или на нуль.

5= 4+1=4*1+2*0+1*1  - цифра 5 соответствует двоичному коду 101

4= 4*1+2*0+1*0  - цифра 4 соответствует двоичному коду 100

3 = 2+1=4*0+2*1+1*1 – цифра 3 соответствует двоичному коду 011

 

543₈ = 101 100 011₂

 

Задача 9.

Перевести Е0А3₁₆ в двоичную систему счисления.

Решение.

Каждая цифра(разряд) числа в шестнадцатеричной системе счисления соответствуют четыре цифры (разряда) в двоичной. Поэтому каждая цифра шестнадцатеричного числа получается из суммы соответствующих степеней двойки (8 4 2 1), умноженных на 1 или на нуль.

Е(14) =8+4+2 = 8*1+4*1+2*1+1*0 – цифра Е(15) соответствует двоичному коду 1110

0 = 8*0+4*0+2*0+1*0 – цифра Е(15) соответствует двоичному коду 0000

А(10) =8+2 = 8*1+4*0+2*1+1*0 – цифра А(10) соответствует двоичному коду 1010

3 =2+1 = 8*0+4*0+2*1+1*1 – цифра 3 соответствует двоичному коду 0011

 

Е0А3₁₆ = 1110 0000 1010 0011₂

 

Задача 10.

Сколько значащих нулей содержит двоичная запись числа 3F1₁₆ ?

Решение.

3F1₁₆ = 0011 1111 0001₂

Два первых нуля данного числа служат дополнением к тераде. Они не являются значащими, потому что их можно откинуть (с левой части числа). Поэтому данное число содержит 3 значащих нуля.

 

Задача 11.

Найти сумму чисел 1В₁₆  и 235_8. Ответ дать в десятичной системе счисления.

Решение.

1В₁₆ = 1*16¹+ 10(В)*16⁰ = 26

235₈ = 2*8²+3*8¹+5*8⁰ = 157

26+157 = 183.

Задача 12.

Для ко­ди­ро­ва­ния букв X, Е, Л, О, Д ре­ши­ли ис­поль­зо­вать дво­ич­ное пред­став­ле­ние чисел 0, 1, 2, 3 и 4 со­от­вет­ствен­но (с со­хра­не­ни­ем од­но­го не­зна­ча­ще­го нуля в слу­чае од­но­раз­ряд­но­го пред­став­ле­ния). Если за­ко­ди­ро­вать по­сле­до­ва­тель­ность букв ЛЕ­ДО­ХОД таким спо­со­бом и ре­зуль­тат за­пи­сать шест­на­дца­те­рич­ным кодом, то по­лу­чит­ся

 

1) 999С

2) 3254145

3) 123F

4) 2143034

 

Решение.

Сна­ча­ла сле­ду­ет пред­ста­вить дан­ные в усло­вии числа в дво­ич­ном коде:

Х	Е	Л	О	Д
0	1	2	3	4
00	01	10	11	100

Затем за­ко­ди­ро­вать по­сле­до­ва­тель­ность букв: ЛЕ­ДО­ХОД — 1001100110011100. Те­перь разобьём это пред­став­ле­ние на четвёрки спра­ва на­ле­во и пе­ре­ведём по­лу­чен­ный набор чисел сначала в де­ся­тич­ный код, затем в шест­на­дца­те­рич­ный.

 

1001 1001 1001 1100 — 9 9 9 12 — 999С.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Задача 13.

Дано: а = 70₁₀, b = 100₈ Какое из чисел с, за­пи­сан­ных в дво­ич­ной си­сте­ме, от­ве­ча­ет усло­вию b < с < a?

 

1) 1000000₂

2) 1000110₂

3) 1000101₂

4) 1000111₂

Решение.

Пе­ре­ве­дем числа в дво­ич­ную си­сте­му счис­ле­ния и затем срав­ним их:

1. 70₁₀=1000110₂

2. 100₈=1000000₂

Проведя поразрядное сравнение чисел получаем, что верный ответ №3.

 

Задача 14.

Дано А = A7₁₆, B = 251₈. Най­ди­те сумму A + B.

 

1) 101011000₂

2) 101010100₂

3) 101010110₂

4) 101010000₂

Решение.

Пе­ре­ве­дем числа в де­ся­тич­ную си­сте­му счис­ле­ния, вы­пол­ним сло­же­ние, и пе­ре­ве­дем сумму в дво­ич­ную си­сте­му счис­ле­ния:

 

A7₁₆ = 10⋅16 + 7 = 167₁₀.

251₈ = 2⋅8² + 5⋅8 + 1 = 169₁₀.

336₁₀ = 1⋅2⁸ + 1⋅2⁶ + 1⋅2⁴ = 101010000₂.

 

Также су­ще­ству­ет вто­рой спо­соб:

 

1. Пе­ре­ве­дем числа в дво­ич­ную си­сте­му счис­ле­ния (через три­а­ды и тет­ра­ды). А₂ = 1010 0111,

В₂ = 010 101 001.

1. Вы­пол­ним сло­же­ние дво­ич­ных чисел: 10100111 + 10101001 = 101010000.

 

Задача 15.

Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го числа 501?

Решение.

Пе­ре­ведём число 501 в дво­ич­ную си­сте­му:

 

501₁₀ = 2⁹ + 2⁸ + 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2² + 2⁰ = 111110101₂.

Ответ: 7.

 

Задача 16.

Даны 4 числа, они за­пи­са­ны с ис­поль­зо­ва­ни­ем раз­лич­ных си­стем счис­ле­ния. Ука­жи­те среди этих чисел то, в дво­ич­ной за­пи­си ко­то­ро­го со­дер­жит­ся ровно 6 еди­ниц. Если таких чисел не­сколь­ко, ука­жи­те наи­боль­шее из них.

 

1) 63₁₀·4₁₀

2) F8₁₆+1₁₀

3) 333₈

4) 11100111₂

 

Решение.

Пе­ре­ве­дем числа в де­ся­тич­ную си­сте­му счис­ле­ния:

 

63₁₀·4₁₀ = 252₁₀,

F8₁₆+1₁₀ = 15·16 + 8 + 1 = 249₁₀,

333₈ = 64·3 + 8·3 + 3 = 219₁₀.

 

Пе­ре­ве­дем по­лу­чен­ные числа в дво­ич­ную си­сте­му счис­ле­ния:

 

252₁₀ = 11111100₂ — 6 еди­ниц;

249₁₀ = 11111001₂ — 6 еди­ниц;

219₁₀ = 11011011₂ — 6 еди­ниц;

11100111₂ — 6 еди­ниц.

 

Наи­боль­шее число — 63₁₀*4₁₀.

Задача 17.

Ука­жи­те наи­мень­шее четырёхзнач­ное шест­на­дца­те­рич­ное число, дво­ич­ная за­пись ко­то­ро­го со­дер­жит ровно 5 нулей. В от­ве­те за­пи­ши­те толь­ко само шест­на­дца­те­рич­ное число, ос­но­ва­ние си­сте­мы счис­ле­ния ука­зы­вать не нужно.

Решение.

Четырёхзнач­ное, зна­чит, в дво­ич­ной за­пи­си оно не мень­ше 1000₁₆ = 1000000000000₂. Чем стар­ше раз­ряд, тем боль­ше он при­бав­ля­ет к числу. По­это­му нули стоит ста­вить имен­но в стар­шие раз­ря­ды. Итого по­лу­чим 1000001111111₂ = 107F₁₆.

 

Задача 18.

В си­сте­ме счис­ле­ния с не­ко­то­рым ос­но­ва­ни­ем де­ся­тич­ное число 18 за­пи­сы­ва­ет­ся в виде 30. Ука­жи­те это ос­но­ва­ние.

Решение.

Со­ста­вим урав­не­ние: где 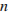— ос­но­ва­ние этой си­сте­мы счис­ле­ния. Ис­хо­дя из урав­не­ния,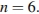

 

---

Дата добавления: 2018-11-24; просмотров: 233; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!