Теорема 1.8.1. (Кронекера-Капелли.)

Система линейных уравнений является совместной тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы В.

Замечание.

Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить ранги матриц, ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.

 

Методы решения систем линейных уравнений.

Метод Крамера и матричный метод.

 

Рассмотрим частный случай системы линейных уравнений, когда m = n, то есть когда число уравнений совпадает с числом неизвестных. Если число уравнений равно числу неизвестных, то матрица А исходной системы - квадратная, порядка, х и b - столбцы высоты n. 

Определение 1.10.1.1. Если 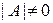, то система называется крамеровской.

Теорема 1.10.1.1. (Крамера)

Крамеровская система совместна и имеет единственное решение.

Доказательство.

Совместность:

Предположим, что 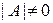. Тогда по 1.6.1 существует обратная матрица. Умножив слева обе части равенства  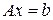на А^-1, получим

 

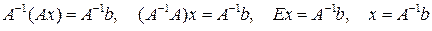
Таким образом, система уравнений имеет решение и оно в матричной форме может быть записано в виде

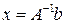
Это так называемый матричный способ решения системы линейных уравнений.

Единственность:

Рассмотрим произвольное решение системы 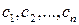 и подставим эти числа в систему вместо неизвестных, тогда система имеет вид

.

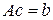Аналогичным способом получим, что 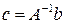. Таким образом, любое другое решение системы имеет такой же вид, значит решение единственно.

 

Введем следующие обозначения. Пусть 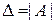, - определитель матрицы, полученной из матрицы А заменой столбца с номером i на столбец b свободных членов, :

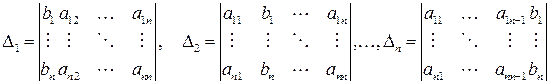
По теореме 1.6.1.

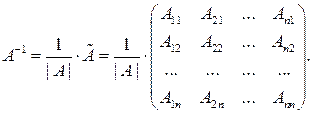
где 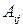 - алгебраические дополнения. Тогда

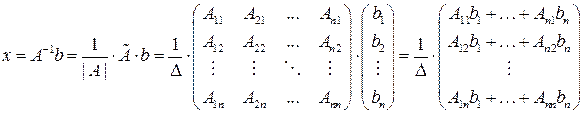. Заметим, что по формулам следствия 1 из теоремы Лапласа разложение определителя  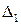по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя  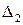по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому 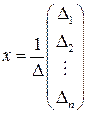, откуда следует, что решение крамеровской системы может быть найдено по формулам:

Это так называемый метод Крамера решения системы линейных уравнений.

 

Пример 10.1.

Решить систему матричным методом.

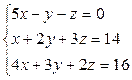
Решение.

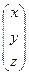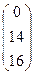x = , b= , A = .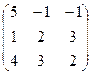

Обратная матрица была найдена ранее, поэтому

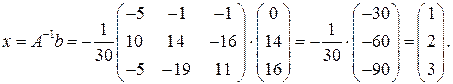
Ответ: х₁=1, х₂=2, х₃=3.

 

 

Пример 10.2.

Решить предыдущую систему методом Крамера.

Решение.

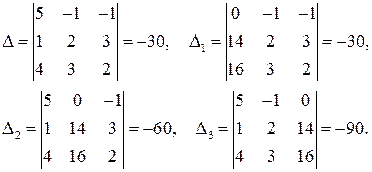
Таким образом,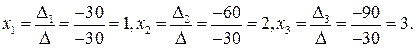

Метод Гаусса

 

Пусть дана система m линейных уравнений с n неизвестными 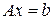. Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

 

Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода. Сам метод близок к методу вычисления определителя 1.3 и к методу нахождения ранга матрицы 1.7.

Прямой ход состоит в приведении матрицы к верхнее треугольному или трапециидальному виду.

1-й шаг. Целью этого шага является исключение неизвестного x₁ из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a₁₁ ¹ 0.

Найдем величины

q_i1 = a_i1/a₁₁ (i = 2, 3, …, n),

называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n -го уравнений системы первое уравнение, умноженное соответственно на q ₂₁, q₃₁, …, q_n1. Это позволит обратить в нуль коэффициенты при x₁ во всех уравнениях, кроме первого. В результате получим эквивалентную систему

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1n x_n = b₁ ,

a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a_2n⁽¹⁾x_n = b₂⁽¹⁾ ,

a₃₂⁽¹⁾x₂ + a₃₃⁽¹⁾x₃ + … + a_3n⁽¹⁾x_n = b₃⁽¹⁾ ,

. . . . . . . . . . . . . . .

a_n2⁽¹⁾x₂ + a_n3⁽¹⁾x₃ + … + a_nn⁽¹⁾x_n = b_n⁽¹⁾ .

в которой a_ij⁽¹⁾ и b_ij⁽¹⁾ вычисляются по формулам

a_ij⁽¹⁾ = a_ij − q_i1a_1j    , b_i⁽¹⁾ = b_i − q_i1b₁.

2-й шаг. Целью этого шага является исключение неизвестного x₂ из уравнений с номерами i = 3, 4, …, n. Пусть a₂₂⁽¹⁾ ≠ 0. Вычислим множители 2-го шага

q_i2 = a_i2⁽¹⁾ / a₂₂⁽¹⁾ (i = 3, 4, …, n)

и вычтем последовательно из третьего, четвертого, …, n -го уравнения системы второе уравнение, умноженное соответственно на q₃₂, q₄₂, …, q_m2. В результате получим систему

     a₁₁x₁ + a₁₂x₂ + a₁₃x₃ +     … + a_1n x_n =   b₁     ,

                  a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … +   a_2n⁽¹⁾ =   b₂⁽¹⁾ ,

                             a₃₃⁽²⁾x₃ +   … + a_3n⁽²⁾x_n = b₃⁽²⁾ ,

. . . . . . . . . . . . . . . . . . .

                             a_n3⁽²⁾x₃ +   … + a_nn⁽²⁾x_n = b_n⁽²⁾ .

Здесь коэффициенты a_ij⁽²⁾ и b_ij⁽²⁾ вычисляются по формулам

a_ij⁽²⁾ = a_ij⁽¹⁾ – q_i2a_2j⁽¹⁾ , b_i⁽²⁾ = b_i⁽¹⁾ – q_i2b₂⁽¹⁾.

Аналогично проводятся остальные шаги до тех пор, пока не дойдём до последнего уравнения:

     a₁₁x₁ + a₁₂x₂ + a₁₃x₃ +       … + a_1nx_n = d₁     ,

                  a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a_2n⁽¹⁾x_n =d₂ ,

. . . . . . . . . . . . . . . . . . . .

                             c_rrx_r +        … + c _rn⁽²⁾x_n =d _r   ,

     . . . . . . . . . . . . . . . . . . . .

                        0=d_r+1,

. . . . . . . . . . . . . . . . . . . .

                                                   0=d_n.

Возможны три случая:

1) хотя бы одно из чисел d_{r +1}, … d_n отлично от нуля, тогда система несовместна из-за неравенства рангов основной и расширенной матриц системы.

2) d_{r +1}=0, … d_n=0 и r = n . Тогда система совместна и имеет единственное решение, которое находится обратным ходом:

Из последнего уравнения системы находим x_n. Подставляя найденное значение x_n в предпоследнее уравнение, получим x_n–1. Осуществляя обратную подстановку, далее последовательно находим x_n–2, …, x₁. Вычисления неизвестных здесь проводятся по формулам.

3) d_{r +1}=0, … d_n=0 и r < n . Система совместна и имеет бесконечное множество решений. Чтобы решить эту систему n - r перменных х _r+1,…, x_n придаются произвольные значения (такие переменные называются свободными), а все остальные неизвестные выражаются через них, начиная с последнего нетривиального уравнения. Эти выражения и задают все решения системы.

 

На практике, все преобразования удобнее осуществлять с расширенной матрицей системы, одновременно определяя и её ранг.

 

Пример 10.3.

Исследовать систему на совместность и, в случае совместности, решить её.

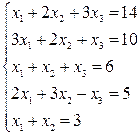
Решение.

Расширенная матрица

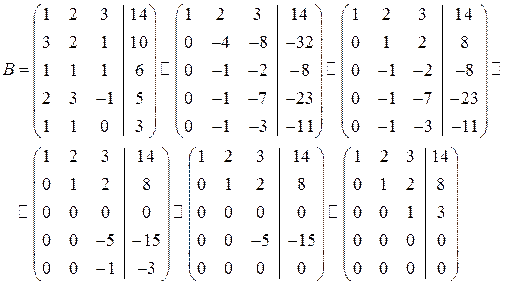
Таким образом, 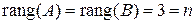, а значит система имеет единственное решение.

 

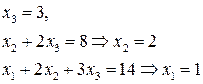
Пример 10.4.

Исследовать систему на совместность и, в случае совместности, решить её.

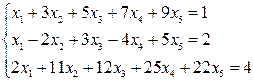
Решение.

Расширенная матрица В = 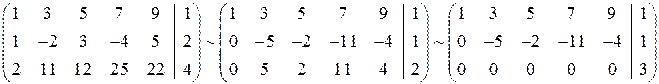    Из последней матрицы видно, что 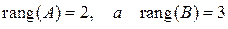, значит система несовместна.

 

Пример 10.5.

Исследовать систему на совместность и, в случае совместности, решить её.

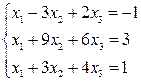
Решение.

Расширенная матрица В=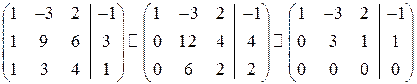

Тогда 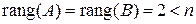, отсюда следует, что система совместна и имеет бесконечное множество решений:

х₃ принимает произвольные значения,

,

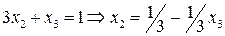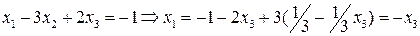
Ответ: 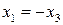, , х₃=с.

 

 

---

Дата добавления: 2018-11-24; просмотров: 209; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!