Миноры и алгебраические дополнения.

Тема 1. Линейная алгебра

Матрицы

Определение 1.1.1.Матрицей А размера  называется совокупность  чисел, расположенных в виде таблицы, состоящей из m строк и n столбцов.

           

 Краткие обозначения матриц: . Элемент матрицы a_ij - число, расположенное в i-ой строке и j-ом столбце.

Определение 1.1.2. Квадратная матрица – матрица с одинаковым числом строк и столбцов (m = n).

Типы квадратных матриц:

1) Диагональная .

    2) Единичная

           

3) Верхняя треугольная   (А) и  нижняя треугольная (В) 

           

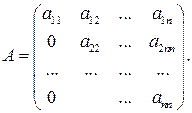
Определение 1.1.3. Нулевая матрица – матрица, все элементы которой равны нулю

                                           .

Определение 1.1.4. Матрица-строка (вектор-строка) – матрица размера

                                          .

Определение 1.1.5. Матрица-столбец (вектор-столбец, m-мерный вектор) – матрица размера .

                                                       .

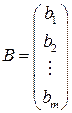Определение 1.1.6. Симметрическая матрица – квадратная матрица, элементы которой, симметричные относительно главной диагонали , равны между собой, т.е. : .

 

Определение 1.1.7. Две матрицы А и В равны между собой, если их размерности совпадают и равны их соответствующие элементы.     

,

 

С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.)

 

Ресурсы	Отрасль экономики
	промышленность	сельское хозяйство
Электроэнергия Трудовые ресурсы Водные ресурсы	5,3 2,8 4,8	4,1 2,1 5,1

 

может быть записана в более компактной форме в виде матрицы распределения ресурсов по отраслям:

                     .

В этой записи, например, матричный элемент а₁₁=5,3 показывает, сколько электроэнергии потребляет промышленность, а элемент а₂₃=5,1 показывает, сколько водных ресурсов потребляет сельское хозяйство.

Операции над матрицами

1.2.1 Сложение матриц. Суммой двух матриц А = (a _ij) и В = (b _ij) одинаковой размерности называется матрица С = (c_ij) той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц А и В (т.е. складываются матрицы поэлементно)

.

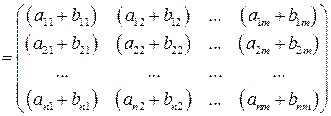Замечание: складывать можно только матрицы одинакового размера.

 

1.2.2 Умножение матрицы на число.  Произведением матрицы А на действительное число  называется матрица той же размерности, полученная из А умножением всех ее элементов на число .

.

 

1.2.3 Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: А-В=А+(-1)·В

Свойства линейных операций:

1) коммутативность ;

2) ассоциативность .

3) .

4) .

5) дистрибутивность относительно сложения матриц .

6) дистрибутивность относительно сложения чисел .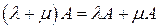

7) ассоциативность по умножению на число .

8)

(А, В, С, 0 одинаковой размерности).

 

Пример 2.1.

Пусть , . Найдем :

 

 1.2.4 Умножение матриц.Произведением матрицы А размера  на матрицу В размера  называется матрица С размера , каждый элемент которой c _ij равен сумме произведений элементов i-ой строки матрицы А на элементы j-ого столбца матрицы В.

    Замечание: Произведение матриц А и В существует (определено), если количество столбцов матрицы А равно количеству строк матрицы В.

Пример 2.2.

Даны матрицы , . Найдите произведения АВ и ВА.

Решение. Рассмотрим произведение АВ. Число столбцов в первом сомножителе А равно 3, число строк во втором сомножителе В тоже равно 3. Числа совпали, следовательно, произведение определено.

Результатом умножения будет матрица С, С=АВ, у которой строк столько, сколько их в первом сомножителе, то есть 3, а столбцов столько, сколько их во втором сомножителе, то есть 2. Итак, матрица С имеет размеры 3´2.

Находим элемент . В его вычислении участвует первая строка 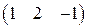 первого сомножителя А и первый столбец  второго сомножителя В:

.

Аналогично находим остальные элементы С.

Итак, .

Рассмотрим произведение ВА. Число столбцов в первом сомножителе В равно 2, число строк во втором сомножителе А равно 3. Числа не совпали, следовательно, произведение не определено.

Ответ: , произведение ВА не определено.

Свойства операции умножения матриц (для А, В, С, Е согласованных размерностей):

1) умножение матриц не коммутативно

Для прямоугольных матриц мы убедились в этом свойстве на предыдущем примере. Проверим выполнение этого свойства для квадратных матриц:

Пример 2.3.

Пусть , . Тогда

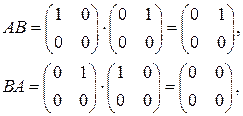
      то есть АВ ¹ ВА.

2) дистрибутивность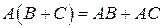

3) дистрибутивность

4) ассоциативность

5)

1.2.5 Возведение в степень. Целой положительной степенью А ^m (m>1)квадратной матрицы А называется произведение m матриц, равных А, т.е.

                               А ^m = (m раз)

Пример 2.4. Найти А², где .

Решение. А²= .

 

1.2.6 Транспонирование матрицы.Транспонирование – операция преобразования матрицы А размера 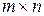 в матрицу А^Т размера 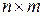, заключающаяся в замене строк А ее столбцами при сохранении их нумерации.

Пример 2.5.

 

Свойства операции транспонирования:

1) .

2) .

3) .

4) .

5) Если А – симметрическая, то .

6) Для любой матрицы А  и  всегда симметрические.

 

Определители

Необходимость введения определителя – числа, характеризующего квадратную матрицу А, – тесно связана с решением систем линейных уравнений.

Определение 1.3.1.Определителем п-ого порядка квадратной матрицы А

                                

называется число ∆ ( ), равное сумме n!=1×2×3×…× n слагаемых, каждое из которых – это произведение n элементов каждой строки и каждого столбца вида , где (количество инверсий) –  количество пар среди , в которых большое число предшествует меньшему.

    Определителем матрицы 1-го порядка А=(а₁₁), или определителем первого порядка, называется элемент а₁₁: 

.

Определитель 2-го порядка:

Определитель 3-го порядка:

.

При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников (правилом Сарруса). Это правило проиллюстрируем на схеме.

Три положительных члена определителя представляют собой произведение элементов главной диагонали (a₁₁a₂₂a₃₃) и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны главной диагонали (a₂₁a₃₂a₁₃ и a₁₂a₂₃a₃₁).

Три отрицательных его члена есть произведения элементов, побочной диагонали (a₁₃a₂₂a₃₁) и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали (a₁₂a₂₁a₃₃ и a₁₁a₂₃a₃₂).

Пример 3.1.

Вычислить определитель .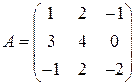

Решение.

Свойства определителей

1) Величина определителя не меняется при его транспонировании .

     Пример 4.1.

     , т.к. это определители транспонированных матриц.

2) Определитель с нулевой строкой или нулевым столбцом равен нулю.

     Пример 4.2.

     , т.к. третий столбец нулевой.

3) Общий множитель какой-либо строки или столбца можно выносить за знак определителя

           

      Пример 4.3.

       

    - общий множитель первого столбца вынесли за знак определителя.

4) При перестановке местами двух строк или двух столбцов определитель меняет свой знак на противоположный.

     Пример 4.4.

    

5) Определитель с двумя одинаковыми строками или столбцами равен нулю.

     Пример 4.5.

     , т.к. одинаковые первый и второй столбцы.

6) Определитель с двумя пропорциональными строками или столбцами равен нулю.

     Пример 4.6.

    

– вторая и третья строки пропорциональны; общий множитель третьей строки вынесли за знак определителя и получили определитель с одинаковыми второй и третьей строками. Этот определитель по свойству 5 равен нулю.

7) Если k-ая строка определителя является суммой каких-либо произвольных строк, то

 Замечание. Это свойство сформулировано для строк определителя, но верно и для столбцов.

8) Величина определителя не изменится, если к элементам какой-либо строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), предварительно умноженные на произвольное число λ (правило преобразования определителя для упрощения вычислений).

Пример 4.7.

Вычислить

 

 (т.к. в полученном определителе 3-я и 4-я строки равны).

9) Определитель произведения двух квадратных матриц одинаковой размерности равен произведению их определителей:

если А, В - квадратные матрицы одинаковой размерности, то .

Пример 4.8.

Найти det(AB), если , .

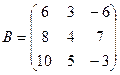Решение.

Матрица В имеет два пропорциональных столбца (первый и второй) и, следовательно, detB=0.

Т.о. 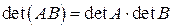 = detA·0 = 0.

10) Определитель диагональной матрицы равен произведению элементов, расположенных на главной диагонали:

11)  Определитель треугольной матрицы равен произведению элементов, расположенных на главной диагонали:

    Таким образом, одним из способов вычисления определителя является приведение матрицы к верхне- или нижнетреугольному виду.

Миноры и алгебраические дополнения.

Определение 1.5.1.Пусть дана квадратная матрица  и некоторое число k, . Зафиксируем произвольные k строк  и k столбцов  Минором порядка k (обозначим М) называют определитель матрицы, составленной из элементов матрицы А на пересечении зафиксированных строк и столбцов.

Пример 5.1.

Пусть дана матрица  и k=2, .

Зафиксируем первую, вторую строки и первый, третий столбцы:

Матрица, составленная из элементов, стоящих на пересечении зафиксированных строк и столбцов, имеет вид:

Тогда

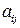Определение 1.5.2.Минор  элемента  - определитель, полученный из исходного определителя  вычеркиванием i-ой строки и j-гo столбца, на пересечении которых расположен элемент .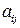

Определение 1.5.3.Алгебраическим дополнением А _ij элемента а _ij матрицы n-го порядка называется его минор, взятый со знаком (-1)^{i + j}:

                                  А _{i j}= (–1)^{i + j} .

Т.о. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца ( i + j ) – чётное число, и отличается от минора знаком, если ( i + j ) – нечётное число.

Пример 5.2. Дана матрица . Найти алгебраическое дополнение элемента а_23.

Решение. Элемент а₂₃ находится на пересечении 2-й строки и 3-го столбца, т.е. i=2; j=3; ( i + j )=2+3=5;   (–1)^{i + j} =(–1)⁵=–1

Минор этого элемента определяем вычёркиванием из определителя матрицы А 2-й строки и 3-го столбца:

                                                

М₂₃= =1×4–3·5=4–15= –11.

Т.о. алгебраическое дополнение А₂₃= (–1)²⁺³М₂₃=(–1)×( –11)=11.

Теорема Лапласа . Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) определителя на их алгебраические дополнения:

∆ = а _{i 1} A_{i 1} + a_{i 2} A_{i 2} +…+ a_inA_in = 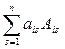                      (5.1)

(разложение по элементам i-й строки; i=1; 2; …;n);

∆=а_{1 j} A _{1 j} + a _{2 j} A _{2 j} +…+ a_njA_nj =                  (5.2) 

(разложение по элементам j-го столбца; j=1; 2; …; n).

Пример 5.3. Вычислим определитель 3 порядка по теореме Лапласа, разложив его по первой строке:

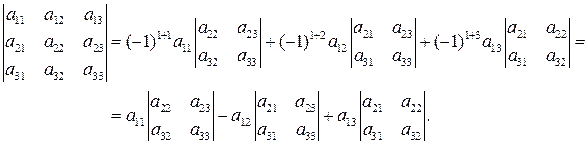
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей n-го порядка к вычислению более простых определителей (n-1) порядка.

 

Следствие. Сумма произведений элементов какой-либо строки на соответствующие алгебраические дополнения другой строки равна нулю.

 

Пример 5.4. Вычислить определитель диагональной матрицы:

 

Решение: Разложим определитель по элементам первого столбца:

=5·(–1)¹⁺¹ +0+0+0 = 5 =5·(–1)( –1)¹⁺¹ +0+0= = 5·(–1)·(3·1–0) = –15.

Обратная матрица

Определение 1.6.1.Квадратная матрица А^-1 называется обратной для квадратной матрицы А, если

.

Определение 1.6.2.Матрица А называется невырожденной, если 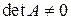. Матрица А обратима тогда и только тогда, когда она невырожденная.

Свойства обратной матрицы:

1)

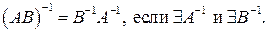
2)

3)

4) .

5)

6) Если  то .

Пример 6.1.

Найти обратную матрицу для A = .

Решение.

|A |=det A = 5(4 – 9) + 1(2 – 12) – 1(3 – 8) = –25 – 10 +5 = –30.

А₁₁ =(-1)²  = -5;  А₂₁ =(-1)⁵  =-1; А₃₁ =(-1)⁴    =-1;

А₁₂ =(-1)³      А₂₂ = (-1)⁴      А₃₂ =(-1)⁵

А₁₃ = (-1)⁴   А₂₃ =(-1)⁵       А₃₃ =(-1)⁶

                    

A^-1 = ;

Проверка .

A×A^-1=    =E.

Ранг матрицы

В этом разделе рассмотрим еще одну важную числовую характеристику матрицы, связанную с тем, насколько ее строки (столбцы) зависят друг от друга.

Определение 1.7.1.Рангом матрицы А называется наибольший из порядков миноров матрицы А, отличных от нуля. Ранг нулевой матрицы считается равным нулю.

Единое, стандартное обозначение ранга матрицы отсутствует, мы будем обозначать его rang(А).

Пример 7.1.

Пусть дана матрица . Она имеет ранг 1, так как только миноры первого порядка отличны от нуля. При составлении миноров второго, третьего и четвертого порядков определитель содержит нулевой столбец, а значит, равен 0.

 

Утверждение 1.7.1. При транспонировании матрицы ее ранг не меняется, то есть .

Определение 1.7.2.Пусть ранг матрицы равен r. Тогда любой минор порядка r, отличный от нуля, называется базисным минором.

Пример 7.2.

Пусть . Определитель матрицы А равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.

Базисным минором является также минор, расположенный, скажем, в первой и третьей строках, первом и третьем столбцах: . Минор в первой и второй строках, втором и третьем столбцах и поэтому не будет базисным. Читатель может самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.

 

Так как столбцы (строки) матрицы можно складывать, умножать на числа, образовывать линейные комбинации, то можно ввести определения линейной зависимости и линейной независимости системы столбцов (строк) матрицы.

Определение 1.7.3.Система столбцов (строк) является линейно независимой, если равенство нулю линейной комбинации этих столбцов (строк) возможна только в случае, когда все коэффициенты этой линейной комбинации равны нулю.

Определение 1.7.4.Система столбцов (строк) называется линейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один отличен от нуля, что линейная комбинация столбцов (строк) с этими коэффициентами будет равна нулю.

Утверждение 1.7.2. Система столбцов (строк) является линейно зависимой тогда и только тогда, когда один из столбцов (одна из строк) является линейной комбинацией других столбцов (строк) этой системы.

Утверждение 1.7.3. Ранг матрицы равен максимальному числу ее столбцов (строк), образующих линейно независимую систему.

Утверждение 1.7.4. Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).

Доказательство.

Пусть дана матрица А размера . Определитель является единственным минором квадратной матрицы, имеющим порядок n. Так как он равен нулю, то . Следовательно, система из n столбцов (строк) является линейно зависимой, то есть один из столбцов (одна из строк) является линейной комбинацией остальных.

Определение 1.7.5.Назовем элементарными преобразованиями матриц следующие действия над ними:

1) перестановка строк или столбцов;

2) умножение строки или столбца на число отличное от нуля;

3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.

Утверждение 1.7.5. При элементарных преобразованиях ранг матрицы не меняется.

Чтобы найти ранг матрицы, удобно привести её к верхнее треугольной, получая нули сначала в первом столбце, потом во втором и т.д, при необходимости меняя местами строки (столбцы). На каком-то этапе мы придем к матрице, у которой все строки, начиная с r +1-ой, равны нулю (или отсутствуют), а минор в первых r строках и первых r столбцах является определителем треугольной матрицы с ненулевыми элементами на диагонали. Ранг такой матрицы равен r. Следовательно, .

Пример 7.3.

Найдите ранг матрицы .

Решение.

=

Базисный минор последней матрицы А стоит в первых трех столбцах и первых трех строках. Следовательно, .

Системы линейных уравнений.

Определение 1.8.1. Системой m линейных уравнений с n неизвестныминазывается система уравнений вида

Система уравнений называется однородной, если  и неоднороднойв противном случае.

 

Наиболее удобной формой записи системы является матричная запись. Введем следующие матрицы: матрица системы А, столбец неизвестных х и столбец свободных членов b.

.

 

C помощью введенных обозначений систему можно записать в виде

Определение 1.8.2. Решением системы называется любой набор чисел , которые при подстановке в систему вместо неизвестных превращают все уравнения системы в верные равенства.

 

Определение 1.8.3. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной – в противном случае, то есть в случае, когда решений у системы нет. Если система имеет единственное решение, то она называется определенной, а если решений бесконечно много – неопределенной.

Вопрос о том, имеет ли система решение или нет, связан не только с соотношением числа уравнений и числа неизвестных.

Примеры 8.1.

1) Рассмотрим 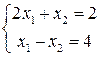. Она совместна и определенная, так как её единственное решение х₁=2, х₂=-2.

2) Рассмотрим . Она несовместна.

3) Однако, система из двух уравнений с тремя неизвестными  имеет бесконечно много решений.

 

Ответ на вопрос о совместности произвольной системы уравнений дает приведенная ниже теорема.

Определение 1.8.4. Расширенной матрицей системы линейных уравнений называется матрица В, отличающаяся от матрицы А системы наличием дополнительного столбца из свободных членов:

 

Утверждение 1.8.1. Ранг расширенной матрицы В либо равен рангу матрицы системы А, либо больше его на единицу.

---

Дата добавления: 2018-11-24; просмотров: 363; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!