Теорема о зависимости значения вероятности события от самого события
Сложение вероятностей двух событий
Умножение вероятностей двух событий
Независимость событий
\\\
*** Теория вероятностей
* Аксиоматическое построение теории вероятностей
Аксиомы теории вероятностей. 1
Теорема о зависимости значения вероятности события от самого события. 2
Условные вероятности. 3
Формула полной вероятности и Формула Бейеса. 5
Аксиомы теории вероятностей
С расширением области применения теории вероятностей возникла необходимость ее аксиоматического построения.
Как в любой аксиоматической теории, выбираются неопределяемые объекты (в нашем случае это события), и строится система аксиом, отражающая свойства этих объектов.
События
Как и многие объекты математики, события можно определить на основе теории множеств.
Согласно определению Колмогорова, имеем множество U элементарных событий. Что представляют собой эти события и какова их природа считаем несущественным.
Далее предполагаем, что фиксирована некоторая система подмножеств множества U. Эти подмножества называют событиями. При этом требуем:
* само множество U есть событие;
* если A – событие, то и ~A (не А) тоже событие (~A – дополнение A до U);
* если A,B,C,… -события, то и их сумма, и их произведение тоже события (под суммой понимают объединение соответствующих компонентов U, а под произведением – их пересечение). Число слагаемых (множителей) может быть и бесконечным.
|
|
|
Система событий, удовлетворяющая перечисленным трем свойствам называется борелевским полем событий или «сигма»-алгеброй.
В задачах, где число элементарных событий конечно, под событием принято понимать все возможные подмножества U, в этом случае все три требования безусловно выполняются.
Два события A и B, не имеющие, как подмножества U, общих элементов, называются несовместными. События A и ~A называются противоположными. Событие U называется достоверным. Событие ~U называется невозможным.
Аксиомы
За аксиомы берутся свойства вероятности, отмеченные на примерах классической и статистической вероятности. Теория является обобщением понятия вероятности.
1). Каждому событию A ставится в соответствие число P(A), называемое вероятностью этого события. 0<=P(A)<=1.
2). Если A, B, C, … набор несовместных событий, то вероятность их суммы равна сумме вероятностей слагаемых. Для бесконечно большого количества слагаемых имеем дело с рядами. Это предложение называют расширенной аксиомой сложения.
2’). (аксиома аддитивности = сложения) Если AÇB=V, то P(AÈB)=P(A)+P(B).
эту аксиому можно методом математической индукции развернуть на счетное число слагаемых.
3). Вероятность события U рана 1.
|
|
|
Перечисленные предложения принимаются без доказательства. Остальные предложения теории вероятностей доказываются.
Пример : P(A)ÈP(~A)=1;
== AÇ~A=V (2’)=> P(AÈ~A) = P(A)+P(~A) = P(U); (3)=> P(A)+P(~A)=1. ==
следствие: P(~U)=P(V)=0.
Теорема : P(AÈB) = P(A) + P(B) – P(A*B)
== A = AÇU = AÇ(BÈ~B) = (AÇB) È (AÇ~B), оба события справа несовместны.
аналогично B = (AÇB) È (~AÇB)
имеем AÈB = (AÇB) È (~AÇB) È (AÇ~B) = B È (AÇ~B), и здесь справа оба события несовместны
Для несовместных событий, согласно аксиоме 2’, имеем:
P(A) = P(AÇB) + P(AÇ~B)
P(AÈB) = P(B) + P(AÇ~B); вычитаем из этого равенства предыдущее, получаем
P(AÈB) – P(A) = P(B) – P(AÇB)
P(AÈB) = P(A) + P(B) – P(AÇB) ==
При классическом определении аксиома 1 содержалась в самом определении, а аксиомы 2 и 3 были доказаны как свойства классической вероятности.
Система аксиом Колмогорова непротиворечива, так как существуют объекты (например, построенные классическим определением), где они выполнены.
Еще один пример: берем квадрат со стороной 1. Испытание заключается в случайном выборе точки квадрата. Событиями будим считать всякие подмножества точек квадрата, для которых имеет смысл понятие площади. Нетрудно проверить, что все аксиомы выполняются.
|
|
|
Система аксиом Колмогорова неполна. Даже для одного и того же множества событий значения вероятностей могут быть разными: например, для игральной кости с 6 гранями можем считать вероятности событий (выпадение 1 .. 6 очков) одинаковыми и равными 1/6 или считать вероятности выпадения нечетных значений равными ¼, а четных = 1/12.
Не следует считать неполноту аксиом свидетельством их неудачного выбора, наоборот, остается возможность «подстройки» теории под реальные объекты.
Теорема о зависимости значения вероятности события от самого события
Теорема: (о непрерывной зависимости вероятности события от события)
Пусть события A1, A2, … таковы, что каждое последующее влечет за собой предыдущее. AiÌAi+1Тогда lim P(n) = P(A), где A = A1ÇA2Ç…
== возьмем некоторый a из A. Возможны два случая: a принадлежит любому из Ai и a принадлежа некоторому Ak не принадлежит A[k+1].
То есть A1 = A È (A1Ç~A2) È (A2Ç~A3) È …
P(A1) = P(A) + P(A1Ç~A2) + P(A2Ç~A3) + … Имеем сходящийся ряд.
Аналогично рассуждая для случая, когда в исходной последовательности отброшены начальные события, получаем: для любого n An = A È (AnÇ~An+1) È (An+1Ç~An+2) È …
P(An) = P(A) + P(AnÇ~An+1) + P(An+1Ç~An+2) + … = P(A)+Rn(A).
|
|
|
Rn(A) – остаток сходящегося ряда и его предел равен 0.
То есть lim P(An) = P(A) + 0. ==
Аксиомы Колмогорова дают удобную математическую схему для исследования некоторых теоретических опытов.
Схема включает в себя три объекта:
* Множество элементарных событий U
* Систему подмножеств U, называемых событиями с операциями суммы и произведения
* Функцию P(A), определенную на множестве событий и удовлетворяющую аксиомам.
Совокупность этих трех компонент называют вероятностной моделью данного опыта.
С появлением системы аксиом появилась возможность определить предмет теории вероятностей в достаточно точных терминах.
Теория вероятностей занимается изучением всевозможных вероятностных моделей.
Задание модели есть задание счетно-аддитивной неотрицательной меры на измеримом пространстве, такой, что m(U)=1.
Как следует из системы аксиом Колмогорова, теория вероятностей есть не что иное, как теория нормированных мер.
Условные вероятности
В основе определения вероятности события лежит некоторая совокупность условий, и, если никаких ограничений, кроме комплекса условий, определяющих испытание, не налагается, то получаемые вероятности называют безусловными.
Рассмотрим ситуацию, когда из ящика, в котором а белых и bчерных шаров, наугад вынимают последовательно один за другим два шара. Рассмотрим события: А — «первый шар белый», В — «второй шар белый».
Понятно, что Р (А) =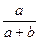 
. Какова же вероятность события В?
Если событие А произошло, то среди оставшихся а+ b—1 шаров только a—1 белых, поэтому вероятность того, что второй шар белый,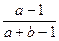 
. Если же А не произошло, то среди оставшихся шаров белых с, поэтому вероятность того, что второй шар белый,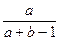 
Мы столкнулись с ситуацией, когда вероятность появления события В зависит от того, произошло или не произошло событие А. В таком случае говорим, что событие В зависит от события А, а вероятность появления события В условная.
Условную вероятность появления события В, если событие А произошло, будем обозначать Р(В|А) или. PA(B)
Найдем способ вычисления таких вероятностей.
Пример: Из колоды карт вынуты две. Найти: безусловную вероятность события, что вторая карта – туз; вероятность события, что вторая карта – туз при условии, что первая карта – туз.
Событие, что вторая карта – туз, распадается на два: «первая карта – туз и вторая карта – туз» и «первая карта не туз, а вторая – туз». Его вероятность P(A) = [(4/36)*(3/35)]+[(32/36)*(4/35)] = (4*3+32*4)/(36*35) = 1/9
Искомой условной вероятностью будет 3/35.
Исходя из классического определения вероятности P(A|B) = r/k = (r/n)/(k/n) = P(AÇB)/P(B)
r – количество случаев наступления события A, при выполнении события B,
k – количество случаев наступления события B.
( Для предыдущего примера P(A|B) = P(AÇB)/P(B) 3/35 = [4/36*3/35]/[4/36] )
Равенство P(A/B) = P(AÇB)/P(B) получено исходя из классического определения вероятности. При аксиоматическом построении оно является определением условной вероятности.
P(A|B) = P(AÇB)/P(B) ; аналогично P(B|A) = P(AÇB)/P(A)
P(AÇB) = P(A|B)*P(B) = P(B|A)*P(A).
Если A и B несовместны (P(AÇB)=0), имеем P(B|A) = P(A|B) = 0.
Условная вероятность тесно связана с понятием независимости событий.
(Для независимых событий P(AÇB) = P(A)*P(B), сравним с определением…)
Событие A не зависит от B, если P(A)=P(A|B).
== Если A не зависит от B, то есть P(A)=P(A|B), то P(A)*P(B)=P(A|B)*P(B)=P(B/A)*P(A), имеем, что P(B)=P(B/A), и событие B не зависит от события A. == Отношение независимости взаимно.
Если A и B независимы, то независимы будут ~A и B; A и ~B; ~A и ~B.
== P(A/B)+P(~A/B)=1 P(A)+P(~A/B)=1 P(~A/B)=P(~A) == доказана независимость ~A и B. Остальные доказываются аналогично.
Для независимых событий P(AÇB) = P(A) * P(B)
Понятие независимости можно расширить на совокупность из n событий.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любой совокупности остальных. Для независимости событий в их совокупности недостаточно, чтобы они были попарно независимы.
Пусть n=3, имеем независимые события А1, А2, А3.
Попарная независимость выражается формулами P(AiÇAj)=P(Ai)*P(Aj) при i<>j.
Для независимости в совокупности выполняются
P(A1|A2ÇA3) = P(A1)*P(A2ÇA3) = P(A1ÇA2ÇA3).
Это более строгое условие, из выполнения которого следует попарная независимость событий. Однако события могут быть попарно независимы, если это равенство и не выполняется.
Пример
Бросаются две монеты. Рассмотрим события: А1 – на первой монете герб, А2 – на второй монете герб, А3 – обе монеты одной стороной.
Всего имеем 4 случая: (герб, герб), (герб, цифра), (цифра, герб), (цифра, цифра).
P(A1)=2/4 = 1/2 P(A2)=2/4 = 1/2 P(A3)=2/4 = 1/2
Имеем, P(AiÇAj) = 1/4 = P(Ai)*P(Aj), но P(A1ÇA2ÇA3)=1/4 <> P(A1)*P(A2)*P(A3)=1/8.
Определить множество независимых события следует так:
События A1, A2, … An независимы, если для любого k<=n справедливо условие
P(А1ÇА2Ç…ÇАk) = P(А1)*P(А2)*…*P(Аk).
В частности, для независимых в совокупности имеет место формула
P(А1ÇА2Ç…ÇАn) = P(А1)*P(А2)*…*P(Аn).
Дата добавления: 2018-11-24; просмотров: 174; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!