Определение параметров функциональных зависимостей
По их графикам
По линейным графикам часто определяется угловой коэффициент изображаемой зависимости. На рис. 5 изображена такая зависимость координаты l от времени t и показано, как определяется её угловой коэффициент Dl/Dt, имеющий размерность скорости.
Также по графикам можно находить производную y ' нелинейной функции y(х). Этот способ определения производной называется методом графического дифференцирования. Метод графического дифференцирования основан на том, что производная равна отношению бесконечно малого приращения функции (dy) к бесконечно малому приращению аргумента (d х):
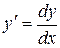 . .
| (15) |
Численное значение производной равно угловому коэффициенту касательной к графику зависимости y(x). Касательная проводится к той точке графика, в которой нужно определить производную (см. рис. 2). Очевидно, что единица измерения производной будет равна отношению единиц измерения величин y и x . На рис. 6 представлен экспериментальный график зависимости температуры Т остывающего нагретого тела от времени t, прошедшего от начала охлаждения. Скорость уменьшения температуры – скорость охлаждения – найдена на графике при температуре 180 °С, до которой охладилось тело за 60 секунд. Производная здесь, конечно, отрицательна, поскольку функция (температура) убывающая. Модуль скорости охлаждения при этой температуре (см. рис. 6) равен 1,12 °С/с.
Контрольные вопросы
|
|
|
1. Чем определяется точность числовых данных в таблице наблюдений? С какой точностью следует производить расчёты?
2. Как определяется число значащих цифр?
3. Как определяются абсолютная и относительная погрешности прямых измерений?
4. До скольких значащих цифр следует округлять значения средних погрешностей измерений?
5. Как проводится кривая (прямая) на графике?
6. Каким требованиям должен отвечать масштаб, нанесенный на осях координат при графической обработке данных?
7. С какой точностью указываются координаты катетов при определении углового коэффициента? В каких единицах измеряется угловой коэффициент?
8. По графику на рис. 7 определите коэффициент упругости пружины.
Механика, молекулярная физика и термодинамика
Работа № 1. Изучение динамики вращательного движения с помощью маятника Обербека
Цель работы: определить значения момента инерции маятника Обербека и момента сил трения для двух вариантов расположения грузиков, проверить закон сохранения энергии.
Оборудование : прибор Обербека, грузы для приведения крестовины во вращение, стойка с делениями, секундомер, штангенциркуль.
Теория метода и описание установки
Для описания вращательного движения твёрдого тела используют кинематические и динамические характеристики, перечисленные в табл. 1.1.
|
|
|
Таблица 1.1
| Кинематические характеристики | Динамические характеристики |
j(t) – угловая координата,
Dj – угловой путь, угол поворота;
 – угловое перемещение; – угловое перемещение;
 – угловая скорость; – угловая скорость;
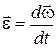 – угловое ускорение – угловое ускорение
| I – момент инерции, кгм2;
для материальной точки I = mr2;
для твёрдого тела 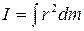 ; ;
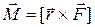 – момент силы;
М = F × l – модуль момента силы, Нм; – момент силы;
М = F × l – модуль момента силы, Нм;
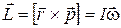 – момент импульса, кгм2/с – момент импульса, кгм2/с
|
В табл. 1.1 m – масса; dm – бесконечно малый элемент массы; r – расстояние от оси вращения;  – радиус-вектор точки приложения силы;
– радиус-вектор точки приложения силы; 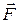 – сила; F – модуль силы; l – плечо силы;
– сила; F – модуль силы; l – плечо силы; 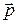 – импульс материальной точки.
– импульс материальной точки.
Динамические характеристики имеют следующий физический смысл:
I – мера инертности при вращательном движении (аналог массы);
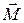 – мера действия при вращательном движении (аналог силы);
– мера действия при вращательном движении (аналог силы);
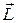 – мера количества движения при вращении (аналог импульса тела).
– мера количества движения при вращении (аналог импульса тела).
Все векторы, характеризующие вращательное движение, направлены по оси вращения в соответствии с «правилом буравчика».
Линейная скорость точки, находящейся на расстоянии r от оси вращения (точнее – модуль скорости 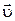 )
)
| u = wr. | (1.1) |
Тангенциальное ускорение
|
|
|
| аt = er. | (1.2) |
Нормальное ускорение
| an = w2r. | (1.3) |
Основной закон динамики вращательного движения тела (аналог II закона Ньютона)
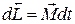 , ,
| (1.4) |
где 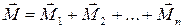 – сумма моментов сил, действующих на тело. Для тела с постоянным моментом инерции
– сумма моментов сил, действующих на тело. Для тела с постоянным моментом инерции
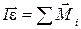 . .
| (1.5) |
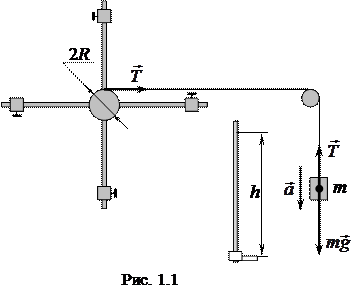 Маятник Обербека, с помощью которого исследуется зависимость между величинами, входящими в выражение основного закона динамики вращательного движения, представляет собой крестовину (рис. 1.1), вращающуюся вокруг горизонтальной оси. На шкив крестовины наматывается нить, к концу которой прикреплён груз массой m.
Маятник Обербека, с помощью которого исследуется зависимость между величинами, входящими в выражение основного закона динамики вращательного движения, представляет собой крестовину (рис. 1.1), вращающуюся вокруг горизонтальной оси. На шкив крестовины наматывается нить, к концу которой прикреплён груз массой m.
При опускании груза сила натяжения нити 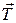 приводит во вращение крестовину. На стержнях крестовины с помощью винтов на равных расстояниях от оси вращения укрепляют четыре одинаковых груза, размеры которых малы по сравнению с их расстоянием от оси вращения.
приводит во вращение крестовину. На стержнях крестовины с помощью винтов на равных расстояниях от оси вращения укрепляют четыре одинаковых груза, размеры которых малы по сравнению с их расстоянием от оси вращения.
Во время движениякрестовина вращается под действием момента 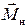 силы натяжения нити. Модуль момента силы натяжения
силы натяжения нити. Модуль момента силы натяжения
| Mн = TR, | (1.6) |
где R – плечо силы 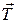 , равное радиусу шкива, на который намотана нить.
, равное радиусу шкива, на который намотана нить.
В рассматриваемом случае на крестовину действует не только сила натяжения нити, но и различные силы трения-сопротивления. Поэтому основной закон динамики вращательного движения (1.5) должен включать в себя и момент сил трения, т.е.
|
|
|
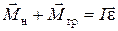 . .
| (1.7) |
Величину вращающего момента легко найти, зная силу натяжения нити и радиус шкива, на который наматывается нить. Из второго закона Ньютона для груза m, опускающегося с ускорением а (см. рис. 1.1), и из выражения (1.6) получаем
| Mн = mR (g – a). | (1.8) |
Ускорение a груза одновременно является тангенциальным ускорением a t точек вращающегося шкива, поэтому из (1.2.) угловое ускорение крестовины
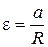 . .
| (1.9) |
Ускорение a и, следовательно, угловое ускорение e можно найти экспериментально, измеряя время t опускания груза с известной высоты h. Ускорение груза легко определяется из кинематического уравнения равноускоренного движения:
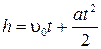 , ,
| (1.10) |
где 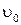 – начальная скорость опускания платформы с грузами.
– начальная скорость опускания платформы с грузами.
Но в уравнении движения (1.7) остаются две неизвестные величины: момент сил трения Mтри момент инерции крестовиныI, так что однозначное решение его при неизменном значении массы груза m невозможно. Однако графически найти и момент инерции, и момент сил трения нетрудно. Для этого следует записать уравнение (1.7) в проекции на ось вращения и привести к известному виду линейной функции y = c + bx. По графику этой функции легко найти постоянные cиb. В нашем случае это будет уравнение
| Mн = Mтр + Ie. | (1.11) |
Проведя измерения с разными массами и построив по данным измерений график зависимости Mнот e, можно найти по нему обе искомые величины: момент инерции Iи обобщённый момент сил сопротивления движению Mтр. Подумайте, как это сделать!
Дата добавления: 2018-11-24; просмотров: 422; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
