Исследование на устойчивость по первому приближению
Определение. Решение системы (1.1) вида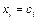 
, 
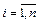, где 
постоянные, называется положением равновесия (или точкой покоя) системы.
Очевидно, что 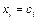, 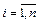- положение равновесия системы (1.1) тогда и только тогда, когда 
, .
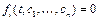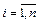Теорема (теорема Ляпунова). Пусть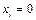 
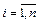, - положение равновесия системы дифференциальных уравнений 
, , 
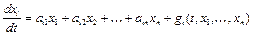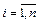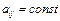(5.1) функции правой части которой удовлетворяют условиям теоремы существования и единственности а функции 
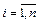при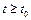 
удовлетворяют условиям 
, 
, 
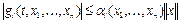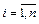, (5.2)
где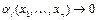 
при 
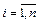, . Тогда если решение 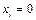, 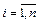системы 
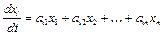(5.3)
устойчиво асимптотически или не устойчиво, то решение 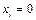, 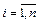системы (5.1) также устойчиво асимптотически или не устойчиво.
Определение. Линейная однородная система дифференциальных уравнений с постоянными коэффициентами (5.3) называется системой первого приближения для системы (5.1).
Систему (5.3) так же называют линеаризацией системы (5.1).
Замечание. Случаи, когда матрица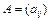 
системы (5.1) не имеет собственных значений с положительной действительной частью, но имеет по крайней мере одно собственное значение с нулевой действительной частью называются критическими. В критических случаях устойчивость или неустойчивость системы (5.1) зависит от вида нелинейных членов системы.
Пусть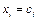 
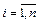, - положение равновесия нормальной системы дифференциальных уравнений (1.1), функции 
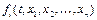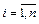, и их частные производные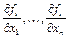 
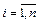непрерывны в некоторой окрестности положения равновесия и эти производные являются постоянными при 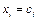, , 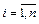т.е. 
, , 
.
|
|
|
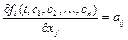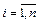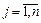Для исследования устойчивости этого положения равновесия сделаем в (1.1) преобразование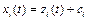 
, 
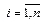. Тогда получим систему 
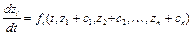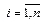, (5.4) с положением равновесия 
, ( 
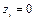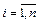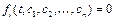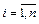, ). В некоторой окрестности положения равновесия 
, 
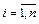можем записать для 
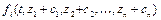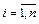, формулу Тейлора
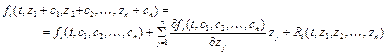, (5.5)
где функции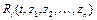 
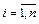, , удовлетворяют условию (5.2). С учётом (5.5) и равенств 
, 
, 
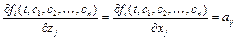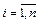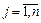систему (5.4) можно записать в виде 
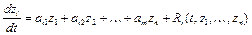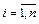, . (5.6)
Пример. Исследуем устойчивость положений равновесия системы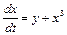 
, 
.
Из уравнений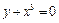 
, 
находим одно положение равновесия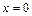 
, 
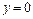данной системы. Исследуем его устойчивость. Поскольку 
, 
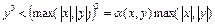и 
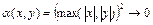при 
, 
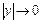, то можно воспользоваться теоремой Ляпунова. Система первого приближения соответствующая положению равновесия имеет вид 
, 
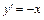. Собственные значения матрицы 
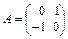этой системы равны 
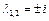. Имеем критический случай (действительные части собственных значений матрицы системы равны нулю), в этом случае, нелинейные члены системы могут влиять на устойчивость положения равновесия.
Дата добавления: 2018-10-27; просмотров: 318; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!