Пример метода 1-х интегралов при решении линейного однородного ДУЧП
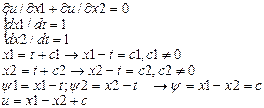
Квазилинейное дифференциальное уравнение в частных производных первого порядка .
Опр.: Квази-линейным ур-ем 1го порядка наз. ур-я 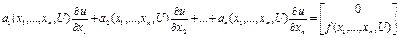 , (3) где ai(x1,…,xn,U), i=1,..,n , f(x1,…,xn,U), i=1,..,n – функции определённые в некоторой обл. D Є Rn+1.
, (3) где ai(x1,…,xn,U), i=1,..,n , f(x1,…,xn,U), i=1,..,n – функции определённые в некоторой обл. D Є Rn+1.
Система уравнений характеристик для квазилинейного уравнения имеет вид:
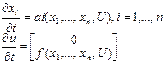 . (4)
. (4)
Те-ма: Если ψi(x1,…,xn)=сi, i=1,..,n первые независимые интегралы уравнений характеристик(4) то все решения ур. (3) определяются из равенства Ф(ψ1,…, ψn)=0.
Пример метода 1-х интегралов при решении квазилинейного ДУЧП
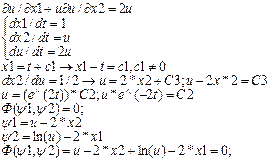
Устойчивость по Ляпунову. Функции Ляпунова. Устойчивость по первому приближению .
Определение функции Ляпунова
Определение. Решение 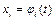 ,
, 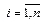 системы (1,1) определённое на
системы (1,1) определённое на 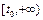 и удовлетворяющее начальным условиям
и удовлетворяющее начальным условиям 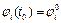 ,
, 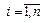 , называется устойчивым по Ляпунову,если для любого
, называется устойчивым по Ляпунову,если для любого  существует
существует 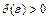 такое, что любое решение
такое, что любое решение  ,
, 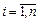 , системы (1), начальные данные
, системы (1), начальные данные 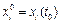
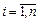 которого удовлетворяют условиям
которого удовлетворяют условиям
 ,
, 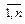 (3.1) определено на
(3.1) определено на 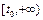 и выполняются неравенства
и выполняются неравенства 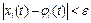 ,
, 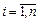 (3.2)
(3.2)
для всех 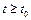 . Если кроме выполнения неравенств (3.2) при условии (3.1) выполняется также условие
. Если кроме выполнения неравенств (3.2) при условии (3.1) выполняется также условие
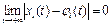 ,
, 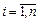 , (3.3), то решение
, (3.3), то решение 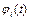 ,
, 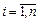 называется асимптотически устойчивым.
называется асимптотически устойчивым.
Если при сколь угодно малом 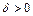 хотя бы для одного решения
хотя бы для одного решения 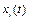 неравенства (3.2) не выполняются, то решение
неравенства (3.2) не выполняются, то решение  ,
, 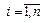 называется неустойчивым.
называется неустойчивым.
Отметим, что из выполнения условий (3.3) не следует устойчивость по Ляпунову.Решение 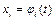
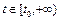 ,
, 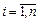 системы (1.1), отвечающее начальным условиям
системы (1.1), отвечающее начальным условиям  ,
, 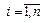 , называют невозмущённым, а решения
, называют невозмущённым, а решения 
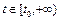 ,
, 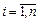 этой же системы при любых других начальных условиях
этой же системы при любых других начальных условиях 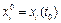 ,
, 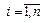 называют возмущёнными.
называют возмущёнными.
|
|
|
Геометрически устойчивость по Ляпунову решения 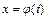 ,
, 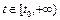 уравнения
уравнения  , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 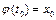 , означает, что сколь угодно узкая
, означает, что сколь угодно узкая 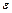 -трубка решения
-трубка решения 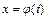 ,
, 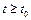 содержит все решения
содержит все решения 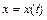 ,
, 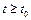 уравнения, которые при
уравнения, которые при 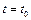 отличаются от
отличаются от 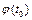 не более чем на
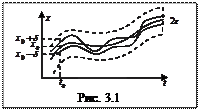
не более чем на 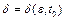 (рис. 3.1). Асимптотическая устойчивость решения
(рис. 3.1). Асимптотическая устойчивость решения 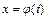 ,
, 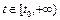 уравнения означает не только близость к нему всех решений
уравнения означает не только близость к нему всех решений 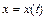 ,
, 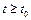 уравнения, вытекающая из близости их к
уравнения, вытекающая из близости их к 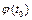 при
при 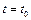 , но и неограниченное сближение их с
, но и неограниченное сближение их с 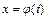 при
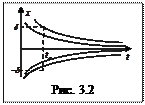
при  . На рис. 3.2 показана асимптотическая устойчивость решения
. На рис. 3.2 показана асимптотическая устойчивость решения 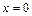 дифференциального уравнения. Исследование устойчивости решения
дифференциального уравнения. Исследование устойчивости решения 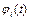 ,
, 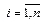 системы (1.1) может быть сведено к исследованию устойчивости нулевого решения. В системе (1.1) введём новые неизвестные функции
системы (1.1) может быть сведено к исследованию устойчивости нулевого решения. В системе (1.1) введём новые неизвестные функции 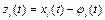 ,
, 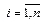 . Очевидно, функции
. Очевидно, функции 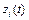 ,
, 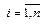 удовлетворяют системе уравнений
удовлетворяют системе уравнений 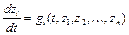 ,
, 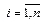 (3.4), где
(3.4), где  ,
, 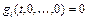 ,
, 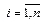 . Устойчивость по Ляпунову (или асимптотическая устойчивость) решения
. Устойчивость по Ляпунову (или асимптотическая устойчивость) решения 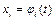 ,
, 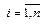 системы (1.1) равносильна устойчивости по Ляпунову (или асимптотической устойчивости) решения
системы (1.1) равносильна устойчивости по Ляпунову (или асимптотической устойчивости) решения  ,
, 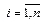 системы уравнений (3.4)
системы уравнений (3.4)
Пример. Исследуем устойчивость решение задачи Коши 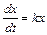 , (
, ( 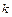 - постоянная),
- постоянная), 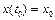 .
.
|
|
|
Общее решение дифференциального уравнения  имеет вид
имеет вид 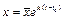 (
( 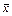 - произвольная постоянная) и определено для всех
- произвольная постоянная) и определено для всех 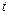 . Решение данной задачи Коши есть
. Решение данной задачи Коши есть 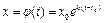 . (3.5). При
. (3.5). При 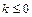 решение (3.5) устойчиво по Ляпунову. При всех
решение (3.5) устойчиво по Ляпунову. При всех 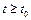 для любого
для любого  и
и 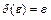 если
если  , то
, то  . При
. При 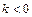
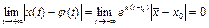 , т.е. решение (3.5) устойчиво асимптотически. При
, т.е. решение (3.5) устойчиво асимптотически. При 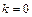
 если
если 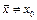 , т.е. решение (3.5) устойчиво по Ляпунову, но не асимптотически устойчиво. При
, т.е. решение (3.5) устойчиво по Ляпунову, но не асимптотически устойчиво. При 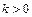 и
и 
 и, следовательно, решение (3.5) неустойчиво.
и, следовательно, решение (3.5) неустойчиво.
Дата добавления: 2018-10-27; просмотров: 270; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
