Метод вариации произвольной постоянной:

Стр 1 из 7Следующая ⇒

Общие понятия теории обыкновенных ДУ 1-го порядка. Теорема о разрешимости задачи Коши. Основные классы ДУ 1-го порядка, решаемых в квадратурах.

Опр.: F(x,y,y’)=0 (1), где x-независимая переменная, у=у(х)- искомая ф-я,y'(x)=dy/dx. Ф-я F-определена в некоторой обл. D Є R³и во всяком случае зависит от у'(х)-нзв. обыкновенным диффер. ур-м 1го порядка.

Опр.: Решениемдиф. ур.(1) на промежутке <a,b> наз. диффер-ый на <a,b> ф-ия у=φ(х) такая что:

1)(х, φ(х), φ'(х))єD, для любого xє<a,b>; 2)F (х, φ(х), φ'(х))=0 для люб. xє<a,b>.

Опр.: Обыкновенное диффер. ур-е 1го порядка y’=f(x,y) (2), где ф-я f-определена в некоторой обл. D Є R² называется д.у. 1-го порядка разрещённым относительно производной.

Задачей Коши (начальной задачей) для ур. (2) наз.задача нахождения решения у=у(х) ур.(2) удовлетворяющего усл-ю у(х₀) = у₀(3), x₀ є <a,b>, у₀-заданные числа.

Частным реш-м диф. ур. наз. решение у=у(х) какой-нибудь задачи Коши поставленной для этого уравнения.

Функцию y=φ(x, С) будем называть общим решением ур. (2), если при произвольном значении постоянной С функция φ обращается в любое решение уравнения, причём все возможные C будут давать всё семейство решений. Общее реш. диф. ур. заданное в неявном виде Ф(х,у,с)=0 наз. общим интегралом диф. ур-ия.

Пр.: ydy=dx/x => y²/2 = ln x+c. Отв.: y²/2 - ln x+c=0 – общий интеграл, а если записать: 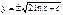- это общее решение.

Теорема Пиано. Если ф-я f(x,y) непрерывна в открытой области D, то для любой точки (х₀, у₀) єD существует решение задачи Коши (2)-(3) определённое в некоторой окрестности точки х₀

Теорема Коши( теор.сущ.и ед-ти) Если функции f(x,y), f_y'(х,y)- непрерывны в открытой области D то для любой точки (х₀, у₀) єD существует единственное решение задачи Коши (2)-(3) определённое в некоторой окрестности точки х₀.

Теорема о разрешимости задачи Коши: Пусть ф-ияf(х, у) определена в области П={(x,y)єR²| |x-x₀|≤a |y-y₀|≤b}непрерывна в П и удовлетворяет усл. Липшеца по у, тогда (2)-(3) имеет реш. у=у(х) определенная на отрезке [x₀-h, x₀+h], где h=min(a,b/M), 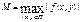и это решение единственно на указанном отрезке.

Основные классы ДУ 1-го порядка, решаемых в квадратурах:

1) Ур-ия с разделенными переменными. Пр.: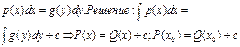

Ур-ия с разделяющимися переменными. Пр .: M₁(x)N₁(y)dx - M₂(x)N₂(y)dy=0

2) Однородные диф. ур-ия 1го порядка.

Опр.: Уравнение M ( x , y ) dx – N ( x , y ) dy = 0 , где M ( x , y ), N ( x , y ) – однородные функции степени n называется однородным.

Опр. Ф-ия F ( x , y ), ( x , y )є D наз. однородной степени n , если для люб. t : ( tx , ty )є D и F ( tx , ty )= t^m ∙ F ( x , y ).

Однородное диф. ур можно записывать в виде y '= f ( y / x ).

Пр.:

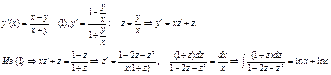
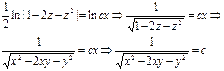
3) Линейные ур-я, ур-ия Бернули.

y’+a(x)y=b(x)–линейные диф. ур., где a(x), b(x)-непрер. на <a,b> ; y’+a(x)y=b(x)y^α(α≠0, α≠1)–ур. Бернули. Линейные уравнения решаются методом вариации произвольной постоянной. Ур-ия Бернули решается с помощью подстановки y=U(x)∙V(x), где U(x)≠0, V(x)≠0 или способом сведения к линейному ур-ию z=y(x)^1-α .

Метод вариации произвольной постоянной:

y’+a(x)y=b(x) (*) 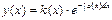– метод Лагранжа (т. е. вариации)

y₀’(x)= - a(x)y₀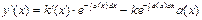

y₀’/ y₀ = -a(x)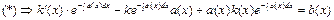

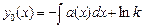
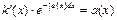
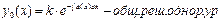
Пр.: y’+y/x=3x k’=3x²

y’/y+1/x=0 k=∫3x²dx

ln y+ln x=ln k(x) k=x³+c

xy=k(x) xy=k(x)=>y= x³/x+c/x

y= k(x)/x y(x) = x²+ c/x

y’ = k’/x - k/x²

k’/x - k/x² + k(x)/x²=3x

5)Ур-ия в полных дифференциалах

Опр.: Ур. в полных дифференциалах–наз. диф. ур. M(x,y)dx+N(x,y)dy=0 (**), левая часть которой есть полный диф-л ф-ии U(x,y) если ðM/ðy= ðN/ðx (#), то ур-е (**) –ур. полных диф-в. Реш д.у. (**): U(x,c)=c. Учитывая что ðU/ðx= M(x,y)=>U(x,y)

= ∫M(x,y)dx+φ(y), где φ(y)-произвольная постоянная.

ðU/ðy=N(x,y)=>( ∫M(x,y)dx)^’_y= φ^’(y)= N(x,y) и нах. Люб. частное реш. φ= φ(y)

пр.: x²y+y

2xydx+(x²+1)dy=0

(2xy)^’_y=( x²+1)^’_x (проверяем условие (#): 2x=2x, т. е. явл. ур-ем полных дифференциалов)

U(x,y)= ∫2xydx+ φ(y)=x²y+ φ(y)

U^’_y=x²+ φ^’(y)= x²+1=> φ^’(y)=1. Ответ: x²y+y=c

Опр.: Пусть д.у. (**) не является д.у. в полных диффер. Функция m(x,y)<>0 после умножения на которую обоих частей д.у. (**) получается уравнение в полных дифф. Называется интегрирующим множ. д.у.(**),

6)ур-я неразрешенные относительно производнойF(x,y,y’)=0

Ур-ие Лагража наз. y=xφ(y')+ψ(y'), φ(y')≠y'; где φ(u),ψ(u) диффер-ые ф-ии.

Ур-е Клеро y=xy'+ψ(y'), ψ(y')<> ay'+b

Решения уравнений в параметрическом виде находим введением параметра р= y' y=ф(x,y')=ф(x,p), после вычисления полного дифференциала обеих частей равенства y(х)=ф(x,p).

36. Общие понятия ДУ высших порядков. Задача Коши. ДУ, допускающие понижение порядка. Общее решение линейного однородного ДУ. Способ Эйлера для случая постоянных коэффициентов.

Обыкновенным дифференциальным уравнением n-го порядка называется соотношение вида F(x, y, y’, y”, …, y⁽ⁿ⁾) = 0 между независимым переменным x, его функцией y и её производными y’, y”, …, y⁽ⁿ⁾. Функция y = φ(x) называется решением (частным) этого ДУ если после замены y на φ(x), y’ на φ’(x), …, y⁽ⁿ⁾ на φ⁽ⁿ⁾(x) оно обращается в тождество. Функцию φ(x, С₁, C₂, …, C_n) будем называть общим решением, если при произвольном наборе постоянных С₁, C₂, …, C_n функция φ обращается в любое решение уравнения. Нахождение решений дифференциального уравнения называют интегрированием этого уравнения.

Задача Коши состоит в нахождении решения ДУ, удовлетворяющего так называемым начальным условиям:

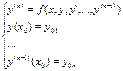
Теорема Пиано

Если f(x,y,y’,…y⁽ⁿ^-1)) непрерывна в открытой области D, то для любой точки (x0, y0, y’0, …y0⁽ⁿ^-1)) существует решение урав-я y⁽ⁿ⁾=f(x,y,y’,…, y⁽ⁿ^-1)) определенной к нектр окрестности точки x0 и удовл.условиям Коши.

Дата добавления: 2018-10-27; просмотров: 231; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!