Теорема Коши (теор.сущ. и единственности)
Пусть f(x,y,y’,…y(n-1)) и ее частные производные df/dy, df/dy’, …,df/dy(n-1) непрерывны в открытой области D, тогда для любой точки y0’ существует единственное решение уравнения y(n)=f(x,y,y’,…, y(n-1)) определенное в нектр окрестности точки x0 и удовл.условиям Коши.
ДУ, допускающие понижение порядка
F(x, y, y’, y”, …, y(n)) = 0 (1)
Опр. Cоотношение вида Ф(x, y, y’, y”, …, y(n-1) ) = С являющееся диффер.уравнением n-1 порядка называется первым интегралом д.у.(1), если при подстановки в него решения y(x) урав. (1), оно обращается в тождество.
Опр. Первые интегралы Фi (x, y, y’, y”, …, y(n-1) , Сi) = 0 i=1..k диффер.ур.(1) называются независимыми, если не существует связи вида ψ (Ф1,…, Фk)=0,
Т-ма. Если известны k независимых первых интегралов д.у. (1) то порядок уравнения (1) можно понизить на k единиц.
Рассмотрим типы уравнений, допускающих понижение порядка( с помощью заме-ны переменной (подстановки) данное ДУ сводится к уравнению, порядок которого ниже)
I) y(n)=f(x)
будем последовательно интегрировать это уравнение, тем самым последовательно понижая степень:
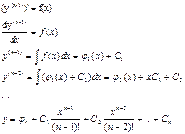
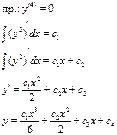
II) F(x, y(k), …, y(n)) = 0, k>=1 ( уравнение не содержит y). Подстановка y(k) =p, p=p(x) – новая неизвестная функция понижает порядок уравнения на k единиц, получим F(x, p, p’, …, p(n-k)) = 0.
ПР. y”=f(x, y’) – это уравнение не содержит y. Подстановка y’=p, p=p(x) – новая неизвестная функция. Тогда у”=p’ и уравнение принимает вид p’=ƒ(х, р). Пусть р=φ(х, C1) – общее решение полученного ДУ первого порядка. Заменяя функцию р на y’, получаем ДУ: y’= φ(х, C1). Для отыскания у достаточно проинтегрировать последнее уравнение. Общее решение начального уравнения будет иметь вид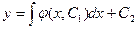 
|
|
|
III) F( y, y’, y”, …, y(n)) = 0 ( уравнение не содержит x). Подстановка y’ =p, p=p(y) – новая неизвестная функция понижает порядок уравнения на единицу, получим F(y, p, p’, …, p(n-1)) = 0.
ПР. y”=f(y, y’) – это уравнение явно не содержит x. Понижаем порядок уравнения подстановкой у’=р(y), р(y)-функция от у. Дифференцируем это равенство по х, учитывая, что р = р(у(х)):
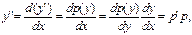теперь уравнение запишется в виде 
.
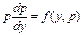Пусть р= φ(y, C1) является общим решением этого ДУ первого порядка. Заменяя функцию р(y) на y’, получаем y’= φ(y, C1) - ДУ с разделяющимися переменными. Интегрируя его, находим общий интеграл начального уравнения: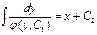 
.
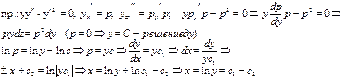
IV) Если уравнение (1) однородно относительно функции y и её производных
т.е. F(x, ty, ty’, ty”, …, ty(n)) = tm F(x, y, y’, y”, …, y(n)), то порядок уравнения можно понизить на единицу подстановкой y’=yz(x), z(x) – новая неизвестная функция.
Т-ма. Если известно m (m<n) линейно независимых решений л.о.д.у.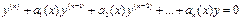 
с непрерывными на (a,b) коэф., то порядок этого уравнения можно понизить на m единиц.
Общее решение линейного однородного ДУ
Опр. Общим решением диф. уравнения на отрезке (a;b) называется функция y = Φ(x, C1,..., Cn ), зависящая от n произвольных постоянныхC1,..., Cn и удовлетворяющая следующим условиям :
|
|
|
− при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn ) является решением уравнения на (a; b);
− какова бы ни была начальная точка (x0, y0, y1,0 ,..., yn − 1,0 ) , x0∈ (a;b) , существуют такие значения C1 =C10 , ..., Cn = Cn0 , что функцияy = Φ(x, C10 , ..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y '(x0) = y1,0 ,..., y(n − 1) (x0) = yn− 1,0 .
Линейным неоднородным д.у. порядка n называется д.у.
, ai (x) – непрерывные на (a; b) функции. (2)
Если f(x)=0 то уравнение (2) называется однородным.
Определ. Система n линейно независимых на (a; b) решений лин. однородного д.у. называется фундаментальной системой решений.
Теорема. Если функции ai (x) – непрерывные на (a; b) , то общее решение л.о.д.у есть функция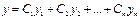 
, где Сi (i=1,... ,n) - произвольные постоянные,{ y1,… yn-}- фундаментальная система решений этого уравнения.
Теорема. Пусть y1,y2,..yn x∈ (a;b) – решения л.о.д.у. Функции y1,y2,..yn линейно независимы на (a;b) тогда и только тогда когда определитель Вронского( вронксиан) W(x)<>0 не равен нулю на (a; b).
.
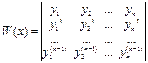Способ Эйлера построения общего решения л.о.д.у. с постоянными коэффициентами
|
|
|
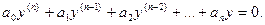
ai – постоянные коэффиценты ЛОДУ. При этом частные решения могут быть найдены в виде y=ekx, где k – постоянная( может быть и комплексным). Действительно, подставляя в начальное уравнение y = ekx и y(p) = kpekx (p=1, 2, …, n), будем иметь:
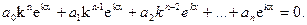
Сокращая на необращающийся в нуль множитель ekx, получим так называемое характеристическое уравнение
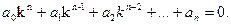
Это уравнение n-й степени определяет те значения k, при которых y=ekx является решением исходного уравнения. Если все корни различны, то найдено n линейно независимых решений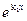 
, 
, …, 
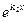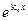. Значит 
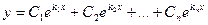, где Сi – произвольные постоянные, является общим решением первоначального уравнения.
Если имеются комплексный корень характеристического уравнения, например k1=α+iβ, он всегда будет идти вместе со своим комплексно сопряжённым k2= α-iβ, то к решению добавится слагаемое: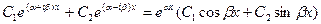 
.
Если имеются кратные корни характеристического уравнения, например имеем m кратных корней k1=k2=…=km=p. тогда к решению добавится слагаемое: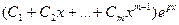 
.
Если имеются кратные комплексные корни характеристического уравнения, например имеем корень p+iq кратности m. А значит и корень p-iq той же кратности. Тогда к решению добавится слагаемое: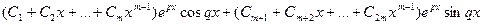 
.
37. Структура общего решения линейного неоднородного ДУ n-го порядка.Метод Лагранжа. Построение частного решения неоднородного ДУ с постоянными коэффициентами при специальной правой части.
|
|
|
Дата добавления: 2018-10-27; просмотров: 191; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!