Основные операции над матрицами
Сложение матриц. Суммой двух матриц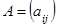 
и 
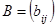одной и той же размерности 
называется матрица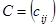 
той же размерности такая, что 
.
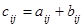Итак, можно складывать только матрицы одной и той же размерности. При сложении матриц складываются соответствующие элементы.
Пример 1.6.
Найдите сумму матриц 
и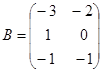 
.
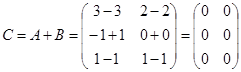— нуль-матрица размерности 
.
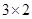Из определения суммы следует, что сложение матриц подчинено:
а) коммутативному закону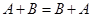 
;
б) ассоциативному закону
;
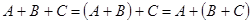в) 
— закон поглощения нуля.
Умножение матрицы на число. Произведением матрицы 
на число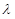 
(или 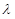на матрицу 
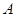) называется матрица 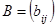, где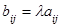 
, т.е. при умножении матрицы на число надо все элементы матрицы умножить на это число.
Пример 1.7.
2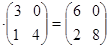 
.
Свойства операции умножения матрицы на число:
а) 
(ассоциативность);
б)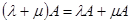 
(дистрибутивность относительно сложения чисел);
в)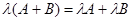 
(дистрибутивность относительно сложения матриц);
г)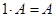 
.
Пример 1.8. Найдит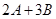е 
, где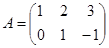 
, 
.
.
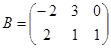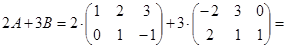
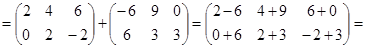
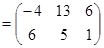
Умножение матриц. Произведением матрицы размерности 
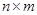на матрицу 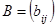размерности 
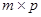называется матрица 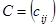размерности 
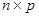такая, что 
, 
, 
.
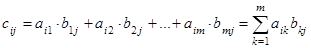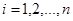Умножать матрицы 
и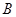 
можно лишь в том случае, когда число столбцов первого сомножителя (число элементов в каждой строке матрицы ) совпадает с числом строк второго сомножителя 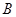(число элементов в каждом столбце 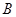). В частности для квадратных матриц одинакового порядка определены оба произведения 
и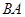 
, и матрицы произведения являются матрицами того же порядка
|
|
|
Пример 1.9. Пусть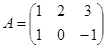 
, 
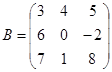. Найдите произведения и 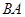(если это возможно).
.
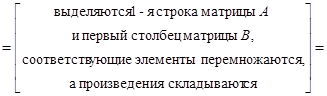
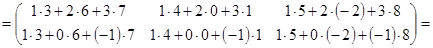
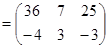Произведение 
не существует, так как число столбцов матрицы не совпадает с числом строк матрицы 
.
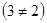Пример 1.10. Пусть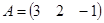 
, 
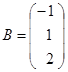. Найдите произведения и (если это возможно).
. 
.
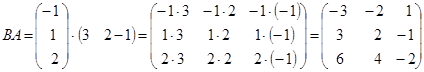Из приведенных выше примеров ясно, что в общем случае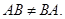 
.
Коммутирующими называют матрицы и 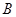, если для них выполнено условие 
.
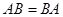Свойства операции умножения матриц:
а) ассоциативность: если определено одно из произведени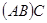й 
или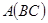 
, то определено также и второе произведение, и имеет место выше приведённое равенство 
;
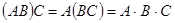б) дистрибутивность: если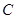 
— такая матрица, что определено произведение 
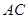, то определены произведения 
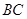и 
и 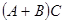верно равенство 
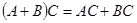( и 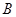— матрицы одинаковых размеров);
в) дистрибутивность: если — такая матрица, что определено произведение , то определены произведения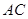 
и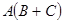 
и верно равенство 
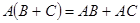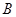( и 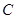— матрицы одинаковых размеров);
г)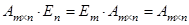 
.
Транспонированная матрица
Транспонированием матрицы называется такое её преобразование, при котором строки этой матрицы становятся её столбцами с теми же номерами.
, 
.
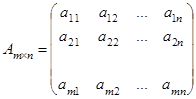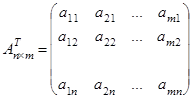Транспонированная матрица обозначается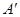 
или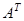 
.
Если 
, т.е.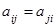 
, то матрица называется симметрической.
|
|
|
Пример Транспонируйте матрицу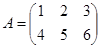 
.
.
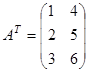4) Собственные векторы и значения матриц
Определение. Число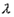 
называется собственным значением квадратной матрицы А, если найдется вектор 
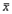такой, что А· 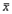= 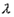· 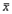. Вектор 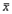называется собственным вектором матрицы А, соответствующим данному собственному значению.
Теорема 1 . Собственные значения матрицы А являются решениями уравнения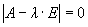 
Это уравнение называетсяхарактеристическим уравнениемматрицы А.
Теорема 2 . Число различных собственных значений квадратной матрицы не превосходит ее порядка. Собственные векторы, отвечающие различным собственным значениям, линейно независимы.
Пример. Пусть дана матрица 
. Составим и решим характеристическое уравнение.
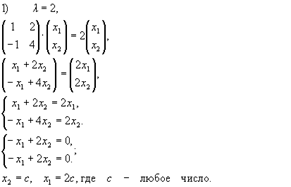
Вектор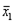 
(2с,с) будет являться собственным вектором, соответствующим собственному значению 2.
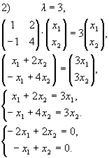
Вектор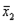 
(с,с) будет являться собственным вектором, соответствующим собственному значению 3.
Векторы 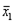(2с,с) и 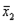(с,с) линейно независимы. Так как они двухмерные, то они образуют базис пространства Е2.
Дата добавления: 2018-10-26; просмотров: 393; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!