Диференціальне числення функцій декількох змінних
Градієнт – вектор, що вказує напрям найбільш швидкої зміни скалярного поля. Якщо плоске поле задане функцією 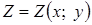 , то градієнт, обчислюваний в його точці
, то градієнт, обчислюваний в його точці 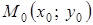 , має вигляд
, має вигляд
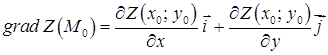 . (2.5.1)
. (2.5.1)
У випадку просторового поля 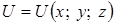 , градієнт в точці
, градієнт в точці 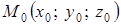 запишеться
запишеться
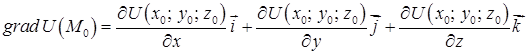 . (2.5.2)
. (2.5.2)
Похідна за напрямом характеризує зміну скалярного поля в напрямі, заданому певним вектором 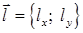 (або у випадку просторового поля
(або у випадку просторового поля 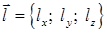 ), і є скалярним добутком градієнта і орта
), і є скалярним добутком градієнта і орта  :
:
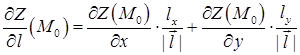 . (2.5.3)
. (2.5.3)
Для просторового скалярного поля похідна за напрямом обчислюється відповідно за формулою
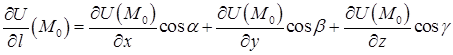 , (2.5.4)
, (2.5.4)
де 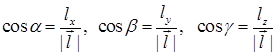 .
.
Градієнт вказує напрям найскорішого зростання функції в заданій точці 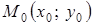 , а у протилежному до градієнта напрямі функція спадає найшвидше. При цьому:
, а у протилежному до градієнта напрямі функція спадає найшвидше. При цьому:
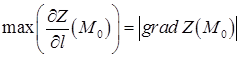 ,
, 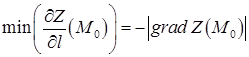 . (2.5.5)
. (2.5.5)
Для визначення точок локальних екстремумів заданої функції  слід спочатку знайти критичні точки (в яких частинні похідні або не існують, або дорівнюють нулеві (стаціонарні точки)). Екстремуми мають місце лише в тих критичних точках, де виконуються достатня умова існування екстремума:
слід спочатку знайти критичні точки (в яких частинні похідні або не існують, або дорівнюють нулеві (стаціонарні точки)). Екстремуми мають місце лише в тих критичних точках, де виконуються достатня умова існування екстремума:
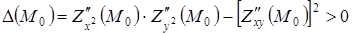 . (2.5.6)
. (2.5.6)
Якщо при цьому 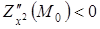 , то екстремум є максимумом;
, то екстремум є максимумом; 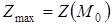 . Якщо при цьому
. Якщо при цьому 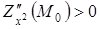 , то екстремум є мінімумом;
, то екстремум є мінімумом; 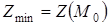 . У випадку
. У випадку 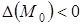 екстремума досліджувана функція в точці
екстремума досліджувана функція в точці 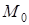 не має. Питання про наявність чи відсутність екстремума в точці
не має. Питання про наявність чи відсутність екстремума в точці 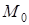 у випадку
у випадку 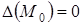 вирішується шляхом подальших досліджень.
вирішується шляхом подальших досліджень.
Приклад 2.5.1. Для функції 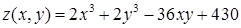 знайти: а) похідну функції за напрямом вектора
знайти: а) похідну функції за напрямом вектора 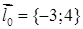 в точці
в точці 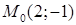 , б) напрям найшвидшого зростання функції в точці
, б) напрям найшвидшого зростання функції в точці 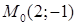 , в) найбільше та найменше значення похідних за напрямом в точці
, в) найбільше та найменше значення похідних за напрямом в точці 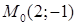 , г) локальні екстремуми.
, г) локальні екстремуми.
|
|
|
Розв’язання. Знаходимо частинні похідні (при цьому, коли шукаємо, наприклад, похідну по 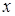 , усі інші змінні вважаються постійними):
, усі інші змінні вважаються постійними):  ,
, 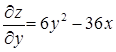 . Таким чином, згідно (2.5.1) градієнт
. Таким чином, згідно (2.5.1) градієнт 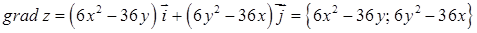 .
.
а) Знаходимо значення градієнта в точці 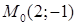 :
:
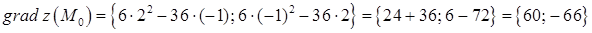 .
.
Довжина вектора напряму згідно (1.2.2): 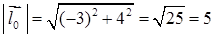 , одиничний вектор напряму :
, одиничний вектор напряму : 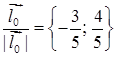 .
.
Похідна функції за напрямом згідно формули (2.5.3):
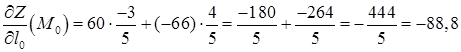 .
.
б) напрям найшвидшого зростання функції в точці 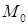 співпадає з напрямом градієнта в цій точці
співпадає з напрямом градієнта в цій точці 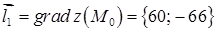 .
.
Довжина градієнта та одиничний вектор напряму найшвидшого зростання функції в точці  :
: 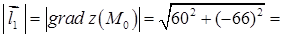
 ,
, 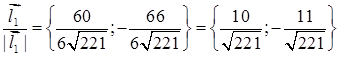 .
.
Відповідно у напрямі 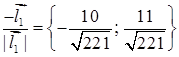 (протилежному до напряму градієнта) функція найшвидше спадає.
(протилежному до напряму градієнта) функція найшвидше спадає.
в) Згідно (2.5.5) серед усіх похідних за напрямом найбільшою є похідна за напрямом градієнта:
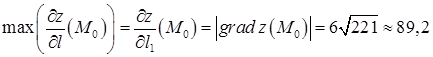 .
.
Найменшою ‑ похідна за напрямом, протилежним до напряму градієнта: 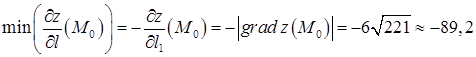 .
.
г) Знайдемо критичні точки. 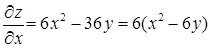 ,
,  . Бачимо, що частинні похідні існують для будь-яких
. Бачимо, що частинні похідні існують для будь-яких 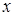 і
і 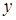 із області визначення функції. Отже, критичні точки є такі, що
із області визначення функції. Отже, критичні точки є такі, що 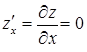 ,
, 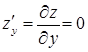 . Таким чином, отримали систему
. Таким чином, отримали систему 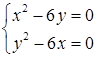 , або
, або 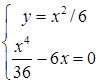 ,
, 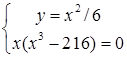 , звідки
, звідки 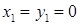 , або
, або 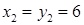 . Отже, у функції є дві критичні точки:
. Отже, у функції є дві критичні точки: 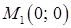 та
та 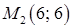 .
.
|
|
|
Перевіримо достатні умови існування екстремума (2.5.6) в кожній з цих точок. Для цого знайдемо частинні похідні другого порядку:
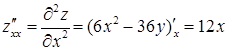 ,
,  ,
, 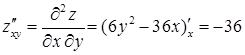 .
.
Значить,  . Таким чином, у точці
. Таким чином, у точці 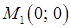 функція екстремума не має.
функція екстремума не має.
В точці 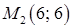 є екстремум, бо
є екстремум, бо 
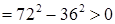 . До того ж екстремум є мінімумом, бо
. До того ж екстремум є мінімумом, бо 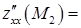
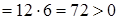 . Значить,
. Значить, 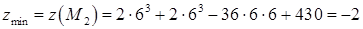 .
.
Література: [1, с. 333 ‑ 360], [2, с. 472 ‑ 494], [3, с. 423 – 431], [10].
МОДУЛЬ 3
Дата добавления: 2018-09-22; просмотров: 258; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
