КОМПЛЕКСНІ ЧИСЛА. ЕЛЕМЕНТИ ТЕОРІЇ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ
Комплексні числа
Комплексним числом називається вираз виду 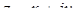 , де
, де 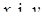 - дійсні числа (тобто
- дійсні числа (тобто 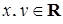 ), а
), а 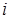 - уявна одиниця (число, квадрат якого дорівнює мінус одиниці:
- уявна одиниця (число, квадрат якого дорівнює мінус одиниці: 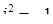 ). Числа
). Числа  і
і 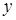 при цьому називаються відповідно дійсною і уявною частиною комплексного числа і позначаються
при цьому називаються відповідно дійсною і уявною частиною комплексного числа і позначаються 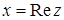 ,
, 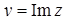 . Вираз
. Вираз  ‑ це алгебраічна форма запису комплексного числа. Множина всіх комплексних чисел позначається
‑ це алгебраічна форма запису комплексного числа. Множина всіх комплексних чисел позначається 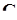 . Дійсні числа можна розглядати як частинний випадок комплексних, тобто
. Дійсні числа можна розглядати як частинний випадок комплексних, тобто 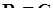 , а саме при
, а саме при 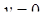 матимемо
матимемо  - дійсне число. Число
- дійсне число. Число 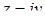 називається суто уявним . Число
називається суто уявним . Число 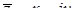 називається спряженим до числа
називається спряженим до числа 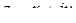 .
.
Приклад 7.1.1. Записати дійсну, уявну частини чисел 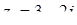 ,
, 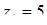 ,
, 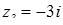 ,
, 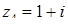 та спряжені до них числа.
та спряжені до них числа.
Розв’язання. Матимемо за означенням: 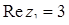 ,
, 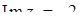 ,
, 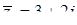 ;
; 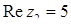 ,
, 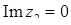 ,
, 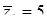 ;
; 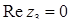 ,
, 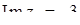 ,
, 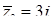 ;
; 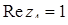 ,
, 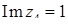 ,
, 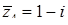 .
.
Сума двох комплексних чисел 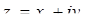 та
та 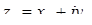 ‑ це число
‑ це число 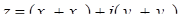 .
.
Приклад 7.1.2. Знайти 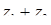 ,
, 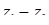 ;
; 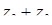 ,
, 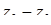 , якщо
, якщо 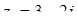 ,
, 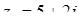 ,
, 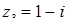 .
.
Розв’язання. Матимемо: 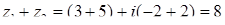 ,
, 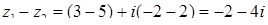 ;
; 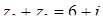 ,
, 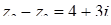 .
.
Комплексні числа перемножуються, як двучлени, при цьому враховується, що 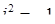 . До речі,
. До речі, 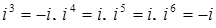 і т.д.
і т.д.
Приклад 7.1.3. Знайти добуток чисел 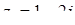 та
та 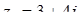 .
.
Розв’язання. 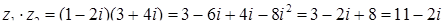 .
.
Частка двох комплексних чисел  і
і 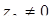 обчислюється за формулою:
обчислюється за формулою:
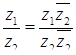 . (7.1.1)
. (7.1.1)
Приклад 7.1.4. Знайти 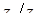 , якщо
, якщо 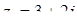 ,
, 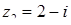 .
.
Розв’язання. За формулою (7.1.1) матимемо:
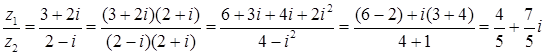 .
.
Комплексне число 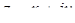 зображується на площині
зображується на площині 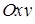 точкою
точкою 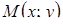 або вектором, початок якого розташований в точці (0; 0), а кінець - у точці
або вектором, початок якого розташований в точці (0; 0), а кінець - у точці 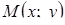 . Модулем комплексного числа
. Модулем комплексного числа 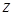 називається невід’ємне число
називається невід’ємне число
|
|
|
 . (7.1.2)
. (7.1.2)
Кут  , який утворює вектор
, який утворює вектор 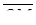 з додатним напрямом осі
з додатним напрямом осі 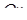 , називається аргументом комплексного числа і позначається
, називається аргументом комплексного числа і позначається 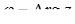 . При
. При  (для
(для 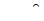 аргумент не визначається) аргумент числа
аргумент не визначається) аргумент числа 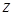 визначається з точністю до доданка, кратною
визначається з точністю до доданка, кратною  . Одне і тільки одне значення
. Одне і тільки одне значення  аргумента
аргумента 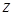 задовольняє умову
задовольняє умову 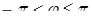 ; воно називається головним значенням аргумента і позначається
; воно називається головним значенням аргумента і позначається  . Отже,
. Отже,  і
і
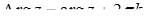
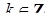 . (7.1.3)
. (7.1.3)
Щоб знайти аргумент, зручно користуватися схемою 7.1.1:
II координатна чверть
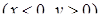 : :
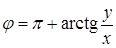
| I координатна чверть
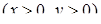 : :
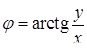
|
III координатна чверть
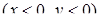 : :

| IV координатна чверть
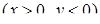 : :
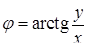
|
Рис. 7.1.1 – Схема визначення 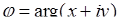
Крім того, якщо 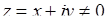 і
і 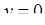 , то
, то 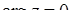 , а якщо
, а якщо  , то
, то 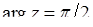 (при
(при 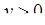 ) і
) і 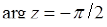 (при
(при 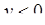 ).
).
(Нагадаємо, що 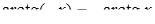 ,
, 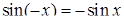 ,
, 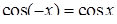 ,
,
 ,
, 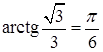 ,
, 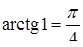 ,
,  ,
, 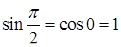 ,
, 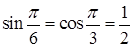 ,
, 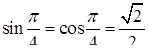 ,
, 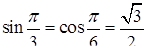 ).
).
Числа 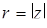 і
і 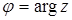 можна розглядати як полярні координати точки
можна розглядати як полярні координати точки 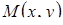 , а тому
, а тому 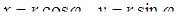 , і комплексне число
, і комплексне число  у тригонометричній формі матиме вигляд:
у тригонометричній формі матиме вигляд:
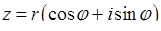 . (7.1.4)
. (7.1.4)
Враховуючи формулу Ейлера
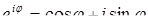 , (7.1.5)
, (7.1.5)
комплексне число  можна представити у формі:
можна представити у формі:
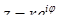 . (7.1.6)
. (7.1.6)
|
|
|
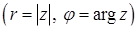 , яка називається показниковою.
, яка називається показниковою.
Приклад 7.1.5. Знайти модулі та аргументи комплексних чисел: 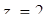 ,
, 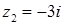 ,
, 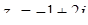 .
.
Розв’язання. За формулою (7.1.2) та схемою 7.1.1: 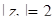 ,
, 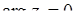 ;
; 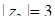 ,
, 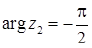 ;
;  ,
, 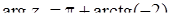 .
.
Приклад 7.1.6. Записати у тригонометричній формі число 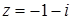 .
.
Розв’язання. За формулою (7.1.2) та схемою 7.1.1: 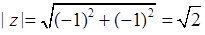 ,
, 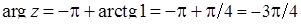 . Отже, згідно (7.1.4):
. Отже, згідно (7.1.4): 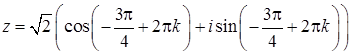 .
.
Якщо 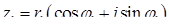 ,
, 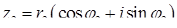 , то
, то
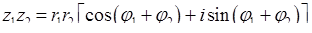 , (7.1.7)
, (7.1.7)
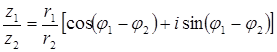 . (7.1.8)
. (7.1.8)
Для натурального 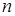 і комплексного
і комплексного  має місце формула Муавра:
має місце формула Муавра:
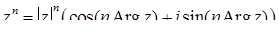 . (7.1.9)
. (7.1.9)
При  існує рівно
існує рівно 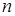 різних значень кореня
різних значень кореня 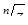 :
:
 , (7.1.10)
, (7.1.10)
де 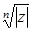 - арифметичний корінь. Ці
- арифметичний корінь. Ці 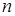 значень зображуються вершинами правильного
значень зображуються вершинами правильного 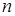 - кутника, вписаного в коло з центром у початку координат і радіусом
- кутника, вписаного в коло з центром у початку координат і радіусом  .
.
Рис. 7.1.2 – Корені комплексного числа
 |
Множина комплексних чисел 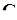 вводиться (як розширення множини дійсних чисел
вводиться (як розширення множини дійсних чисел 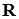 ) таким чином, щоб на ній завжди була здійсненною операція добування кореня.
) таким чином, щоб на ній завжди була здійсненною операція добування кореня.
Наприклад, 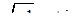 ,
, 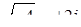 ,
, 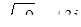 і т.д.,
і т.д., 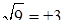 ‑ два значення кореня квадратного (
‑ два значення кореня квадратного ( 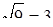 ‑ арифметичне значення кореня).
‑ арифметичне значення кореня).
Приклад 7.1.7. Розв’язати рівняння  .
.
Розв’язання. Квадратне рівняння  має два комплексно спряжених кореня
має два комплексно спряжених кореня 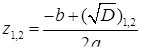 , які не є дійсними числами, якщо дискримінант
, які не є дійсними числами, якщо дискримінант 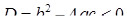 . Наприклад, рівняння
. Наприклад, рівняння 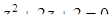 (
(  ) має корені
) має корені 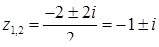 , а рівняння
, а рівняння 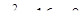 ‑ корені
‑ корені  .
.
|
|
|
Приклад 7.1.8. Розв’язати рівняння  .
.
Розв’язання. Ця задача рівносильна відшуканню значень кореня кубічного 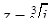 . Визначимо модуль и аргумент числа
. Визначимо модуль и аргумент числа 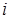 :
: 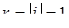 ,
, 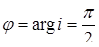 . Тоді за формулою маємо три різних значення кореня кубічного (при
. Тоді за формулою маємо три різних значення кореня кубічного (при  ):
):
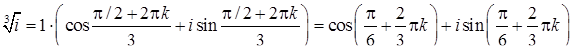 .
.
Виписуємо їх, беручі по черзі  :
: 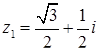 ,
, 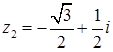 ,
, 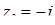 .
.
Для геометричного представлення знайдених значень кореня достатньо зобразити одне значення, наприклад 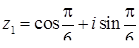 (при
(при  ) ‑ це точка кола радіусу
) ‑ це точка кола радіусу 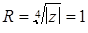 , що лежить на промені
, що лежить на промені 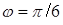 . Після цього будуємо правильний трикутник, вписаний у коло:
. Після цього будуємо правильний трикутник, вписаний у коло:
 |
Рис. 7.1.1 – Значення
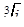 .
.
Приклад 7.1.9. Знайти дійсну і уявну частини комплексного числа 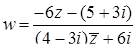 , якщо
, якщо 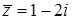 .
.
Розв’язання. Якщо 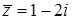 , то
, то  ,
,
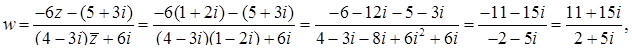
і за формулою (7.1.1): 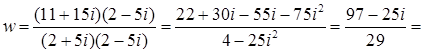
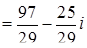 ‑ алгебраічна форма. Таким чином,
‑ алгебраічна форма. Таким чином, 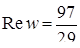 ,
, 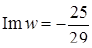 .
.
Зауважимо, що приклад 7.1.9 є аналогічним до завдання 7.1 контрольної роботи.
Література: [1, с. 274 ‑ 278], [3, с. 292 – 299], [16].
Дата добавления: 2018-09-22; просмотров: 220; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
