Неперервні випадкові величини
Неперервною називається випадкова величина, що може приймати будь-які значення з деякого проміжку. Інтегральна функція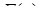 
неперервної випадкової величини 
є неперервною функцією. Неперервні випадкові величини можна задавати також за допомогою диференціальної функції. Диференціальною функцією або щільністю розподілу (щільністю ймовірностей) називається похідна від інтегральної функції:
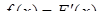(8.3.1)
Властивості диференціальної функції розподілу:
· 
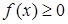, (8.3.2)
· 
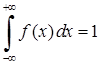, (8.3.3)
· 
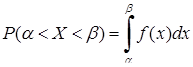, (8.3.4)
· 
(8.3.5)
(зв'язок між диференціальною й інтегральною функціями).
Математичним сподіванням неперервної випадкової величини називається невласний інтеграл
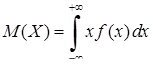, (8.3.6)
де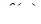 
– диференціальна функція. Якщо випадкова величина 
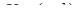, то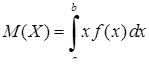 
.
Дисперсіюнеперервної випадкової величини можна обчислити за формулою:
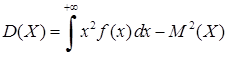, (8.3.7)
причому якщ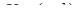о , то 
.
Приклад 8.3.1. Інтегральну функцію розподілу ймовірностей неперервної випадкової величини задано формулою:
|
|
|
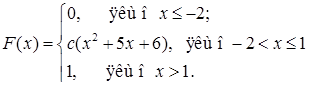
Знайти: а) коефіцієнт с, б) диференціальну функцію 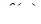, в)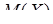 
, 
, 
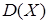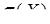, г) ймовірність попадання випадкової величини в інтервал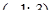 
; д) побудувати графіки функцій 
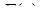і .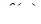
Розв’язання. а), б) Знайдемо диференціальну функцію за формулою (8.3.1):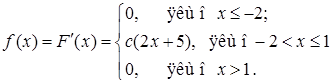 
Коефіцієнт с визначаємо з умови (8.3.3), тобто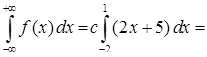 
, значить,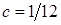 
, отже інтегральна і диференціальна функції набувають вигляду: 
, 
.
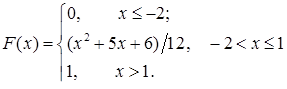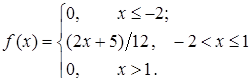в) Знайдемо математичне сподівання випадкової величини та випадкової величини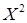 
за формулою (8.3.6):
.
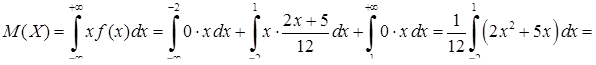
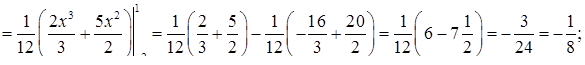
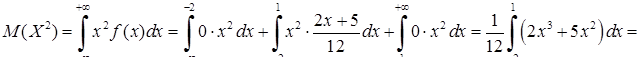
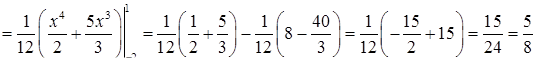Тоді дисперсія за формулою (8.2.9)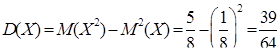 
, середнє квадратичне відхилення за (8.2.14): 
.
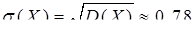г) ймовірність попадання випадкової величини в інтервал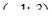 
знайдемо за допомогою інтегральної функції й формули (8.2.4):
.
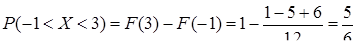Цю ж ймовірність можна обчислити за допомогою диференціальної функції й формули (8.3.4):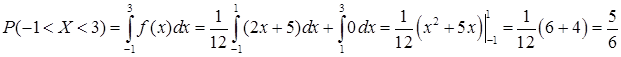 
.
д) графіки диференціальної й інтегральної функції мають вигляд:
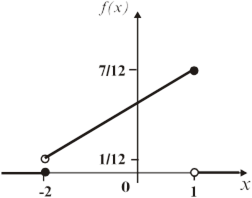
Рис. 8.3.1 – Графік диференціальної функції 
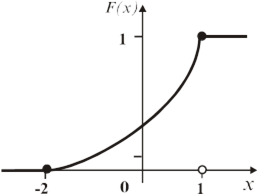
Рис. 8.3.2 – Графік інтегральної функції розподілу 
Література: [1, с. 526 ‑ 529], [4, с. 529 – 559], [16], [18], [20].
Біноміальний та пуассонів закони розподілу
Біноміальним називається розподіл імовірностей дискретної випадкової величини за формулою Бернуллі. Для такої випадкової величини
|
|
|
, 
, 
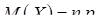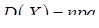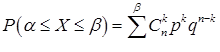. (8.4.1)
Приклад 8.4.1 Знайти математичне сподівання й дисперсію випадкової величини – числа людей, які можуть звернутися до консультанта (з приклада 8.2.1)
Розв’язання. Безпосередній підрахунок числових характеристик цієї випадкової величини, що є біноміально розподіленою, було виконано у прикладі 8.2.1 З іншого боку,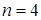 
, 
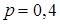
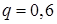, і тому згідно (8.4.1): 
, 
.
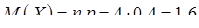Розподілом Пуассона називається розподіл імовірностей дискретної випадкової величини за формулою Пуассона. Для такої випадкової величини
, 
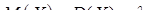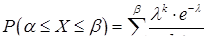(де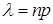 
). (8.4.2)
Закон Пуассона називають також законом рідких подій, він апроксимує біноміальний розподіл при досить великих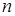 
і малих 
.
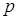Приклад 8.4.2. Прилад містить 2500 мікроелементів, які працюють незалежно друг від друга. Імовірність того, що мікроелемент вийде з ладу під час роботи приладу, дорівнює 0,003. Знайти математичне сподівання, дисперсію й середнє квадратичне відхилення випадкової величини – числа мікроелементів, які вийдуть із ладу під час роботи приладу.
Розв’язання. Випадкова величина розподілена за законом Пуассона з параметром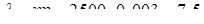 
. Обчислимо її числові характеристики: згідно (8.4.2) 
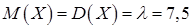, і за формулою (8.2.14) 
.
|
|
|
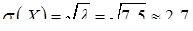Література: [4, с. 563 – 564], [16], [18], [20].
Дата добавления: 2018-09-22; просмотров: 257; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!